Exam 2 - Multiple Choice

In a decision-making setting, if the manager has to contend with limits on the amount of information he or she can consider, this can lead to a poor decision due to _________.

Bounded Rationality

Departmentalizing decisions increases the risk of leading to a poor decision _________.

Suboptimization

Suppose a firm has decided to break its departments down into smaller units. While this likely will help with _________ issues, it raises the possibility that poor decisions will result due to _________.

Span of control; Suboptimization

A decision maker's worst option has an expected value of $1,000, and her best option has an expected value of $3,000. With perfect information, the expected value would be $5,000. What is the expected value of perfect information?

$2,000 | $5,000 - $3,000 = $2,000

The term "suboptimization" is best described as the:

Result of individual departments making the best decisions for their own areas but hurting other areas.

Which phrase best describes the term "bounded rationality"?

Limits imposed on decision making by costs, time, and technology

The range of probability for which an alternative has the best expected payoff can be determined by:

Sensitivity Analysis

Sensitivity analysis is useful because:

Payoffs and probabilities are estimates.

A tabular presentation that shows the outcome for each decision alternative under the various possible states of nature is called a:

Payoff table

Which of the following characterizes decision making under uncertainty?

The likelihood of possible future events is unknown.

Which of the following is not an approach for decision making under uncertainty?

Decision Trees

Determining the worst payoff for each alternative and choosing the alternative with the "best worst" is the approach called:

Maximin

Determining the average payoff for each alternative and choosing the alternative with the highest average is the approach called:

Laplace

The maximin approach to decision making refers to:

Maximizing the minimum return.

Which one of these is not used in decision making under risk?

Minimax Regret

The term "opportunity loss" is most closely associated with:

Minimax Regret

The expected monetary value (EMV) criterion is the decision-making approach used with the decision environment of:

Risk

A decision tree is:

A schematic representation of alternatives.

The difference between expected payoff under certainty and expected payoff under risk is the expected:

Value of perfect information

If the minimum expected regret is computed, it indicates to a decision maker the expected:

Value of perfect information

The term "sensitivity analysis" is most closely associated with:

Decision making under risk

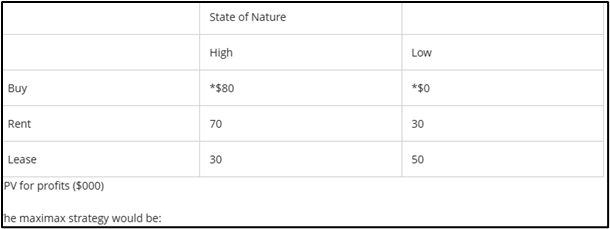
The maximax strategy would be:

Buy | Maximum PV of $80,000 (high)

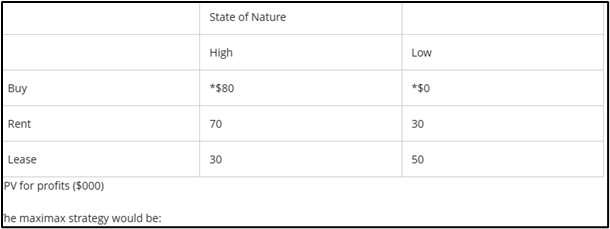
The maximin strategy would be:

Lease | Minimum PV of $30,000 (low)

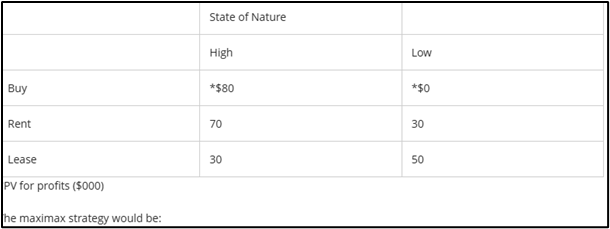
The minimax strategy would be:

Rent | High Max - $80 / Low Max - $50

• Buy -> $50

• Rent -> $20 (min, ans)

• Lease -> $50

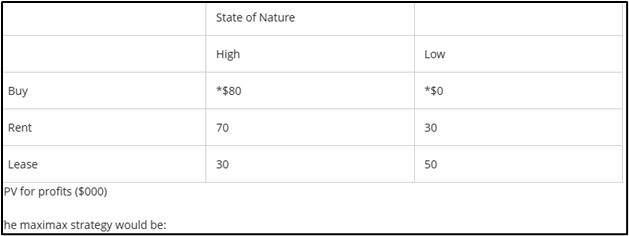
If P(high) is .60, the choice for maximum expected value would be:

Rent | P(high) = 0.6 / P(low) = 1.0

---> 1.0 – 0.6 = 0.4

• Buy -> 0.6($80) + 0.4($0) = $48

• Rent -> 0.6($70) + 0.4($30) = $54 (ans)

• Lease -> 0.6($30) + 0.4($50) = $38

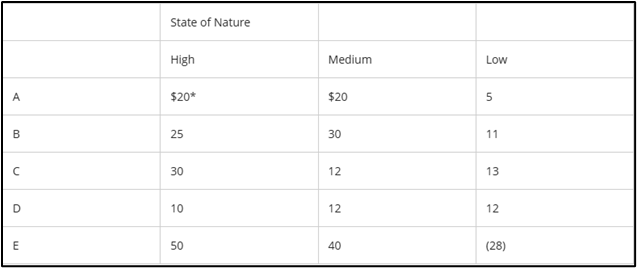
The maximax strategy would be:

E | Maximax PV of $50,000 (High)

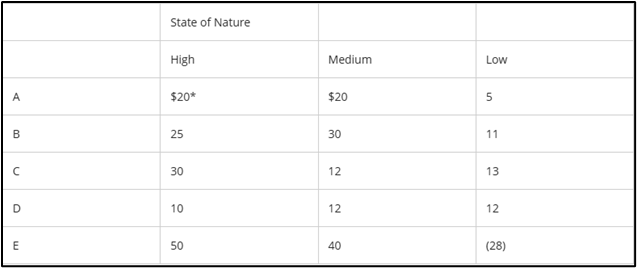
The maximin strategy would be:

C | Maximin PV of $12,000 (Medium)

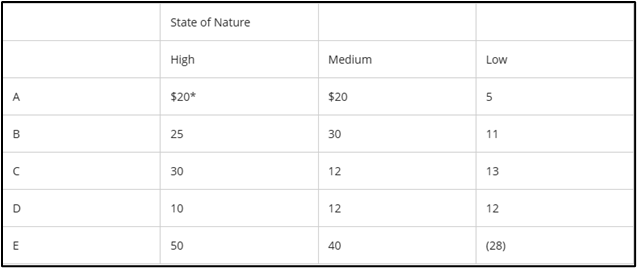
The minimax strategy would be:

B | Minimax of $25,000

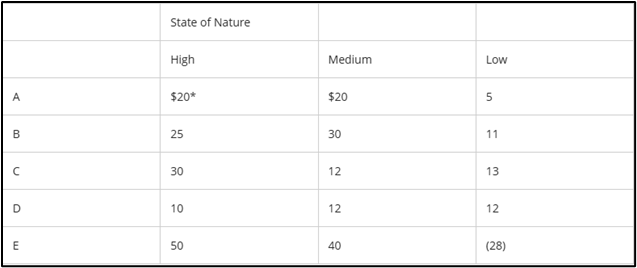
With equally likely states of nature, the alternative that has the largest expected monetary value is:

B | **Follow EMV formula for all rows

The head of operations for a movie studio wants to determine which of two new scripts they should select for their next major production. (Due to budgeting constraints, only one new picture can be undertaken at this time.) She feels that script 1 has a 70 percent chance of earning about $10,000,000 over the long run, but a 30 percent chance of losing $2,000,000. If this movie is successful, then a sequel could also be produced, with an 80 percent chance of earning $5,000,000, but a 20 percent chance of losing $1,000,000. On the other hand, she feels that script 2 has a 60 percent chance of earning $12,000,000, but a 40 percent chance of losing $3,000,000. If successful, its sequel would have a 50 percent chance of earning $8,000,000, but a 50 percent chance of losing $4,000,000. Of course, in either case, if the original movie were a flop, then no sequel would be produced.

What would be the total payoff if script 1 were a success, but its sequel were not?

$9,000,000 | **Success of original movie

The head of operations for a movie studio wants to determine which of two new scripts they should select for their next major production. (Due to budgeting constraints, only one new picture can be undertaken at this time.) She feels that script 1 has a 70 percent chance of earning about $10,000,000 over the long run, but a 30 percent chance of losing $2,000,000. If this movie is successful, then a sequel could also be produced, with an 80 percent chance of earning $5,000,000, but a 20 percent chance of losing $1,000,000. On the other hand, she feels that script 2 has a 60 percent chance of earning $12,000,000, but a 40 percent chance of losing $3,000,000. If successful, its sequel would have a 50 percent chance of earning $8,000,000, but a 50 percent chance of losing $4,000,000. Of course, in either case, if the original movie were a flop, then no sequel would be produced.

What is the probability that script 1 will be a success, but its sequel will not?

.14 | P(original success) x P(1 – original success)

0.7 x 0.2 = 0.14

The head of operations for a movie studio wants to determine which of two new scripts they should select for their next major production. (Due to budgeting constraints, only one new picture can be undertaken at this time.) She feels that script 1 has a 70 percent chance of earning about $10,000,000 over the long run, but a 30 percent chance of losing $2,000,000. If this movie is successful, then a sequel could also be produced, with an 80 percent chance of earning $5,000,000, but a 20 percent chance of losing $1,000,000. On the other hand, she feels that script 2 has a 60 percent chance of earning $12,000,000, but a 40 percent chance of losing $3,000,000. If successful, its sequel would have a 50 percent chance of earning $8,000,000, but a 50 percent chance of losing $4,000,000. Of course, in either case, if the original movie were a flop, then no sequel would be produced.

What is the expected value of selecting script 1?

$9,060,000 | **Follow expected value formula

The head of operations for a movie studio wants to determine which of two new scripts they should select for their next major production. (Due to budgeting constraints, only one new picture can be undertaken at this time.) She feels that script 1 has a 70 percent chance of earning about $10,000,000 over the long run, but a 30 percent chance of losing $2,000,000. If this movie is successful, then a sequel could also be produced, with an 80 percent chance of earning $5,000,000, but a 20 percent chance of losing $1,000,000. On the other hand, she feels that script 2 has a 60 percent chance of earning $12,000,000, but a 40 percent chance of losing $3,000,000. If successful, its sequel would have a 50 percent chance of earning $8,000,000, but a 50 percent chance of losing $4,000,000. Of course, in either case, if the original movie were a flop, then no sequel would be produced.

What is the expected value of selecting script 2?

$7,200,000 | **Follow expected value formula

The head of operations for a movie studio wants to determine which of two new scripts they should select for their next major production. (Due to budgeting constraints, only one new picture can be undertaken at this time.) She feels that script 1 has a 70 percent chance of earning about $10,000,000 over the long run, but a 30 percent chance of losing $2,000,000. If this movie is successful, then a sequel could also be produced, with an 80 percent chance of earning $5,000,000, but a 20 percent chance of losing $1,000,000. On the other hand, she feels that script 2 has a 60 percent chance of earning $12,000,000, but a 40 percent chance of losing $3,000,000. If successful, its sequel would have a 50 percent chance of earning $8,000,000, but a 50 percent chance of losing $4,000,000. Of course, in either case, if the original movie were a flop, then no sequel would be produced.

What is the expected value for the optimum decision alternative?

$9,060,000 | **Follow expected value formula

When a decision-making scenario involves two or more departments, if the individual departments pursue what is optimal for them, sometimes the overall organization suffers. This is an example of:

Suboptimization

Which of the following is not a stage in the decision-making process?

Monitor the competition

Option A has a payoff of $10,000 in environment 1 and $20,000 in environment 2. Option B has a payoff of $5,000 in environment 1 and $27,500 in environment 2. Once the probability of environment 1 exceeds , option A becomes the better choice.

.60 | SOLVE FOR….

(1) 10,000p +20,000 - 20,000p

(2) 5,000p + 27,500 – 27,500p

(3) 20,000 – 10,000p = 27,500 – 22,500p

Which of the following would make decision trees an especially attractive decision-making tool?

The need to think through a possible sequence of decisions.

The linear optimization technique for allocating constrained resources among different products is:

Linear Programming

Which of the following is not a component of the structure of a linear programming model?

Environmental Uncertainty

Coordinates of all corner points are substituted into the objective function when we use the approach called:

Enumeration

Which of the following could not be a linear programming problem constraint?

1A + 2B

For the products A, B, C, and D, which of the following could be a linear programming objective function?

Z = 1A + 2B + 3C + 4D

The logical approach, from beginning to end, for assembling a linear programming model begins with:

Identifying the decision variables

The region which satisfies all of the constraints in graphical linear programming is called the:

Feasible solution space

In graphical linear programming to maximize profit, the objective function is:

        I.    A family of parallel lines

      II.    A family of isoprofit lines

    III.    Interpolated

IV. Linear

I, II, and IV only

Which objective function has the same slope as this one: $4x + $2y = $20?

$4x + $2y = $10

In graphical linear programming, when the objective function is parallel to one of the binding constraints, then:

Multiple optimal solutions exist

The theoretical limit on the number of decision variables that can be handled by the simplex method in a single problem is:

Unlimited

A shadow price reflects which of the following in a maximization problem?

Marginal gain in the objective that would be realized by adding one unit of a resource

In linear programming, a nonzero reduced cost is associated with a:

Decision variable not in the solution

A constraint that does not form a unique boundary of the feasible solution space is a:

Redundant Constraint

In linear programming, sensitivity analysis is associated with:

        I.     A family of parallel lines

      II.     A family of isoprofit lines

III. Interpolated

I, II, and III

In a linear programming problem, the objective function was specified as follows:

 

Z = 2A + 4B + 3C

 

The optimal solution calls for A to equal 4, B to equal 6, and C to equal 3. It has also been determined that the coefficient associated with A can range from 1.75 to 2.25 without the optimal solution changing. This range is called A's:

Range of Optimality

An analyst, having solved a linear programming problem, determined that he had 10 more units of resource Q than previously believed. Upon modifying his program, he observed that the list of basic variables did not change, but the value of the objective function increased by $30. This means that resource Q's shadow price was:

$3.00 | 30/10 = 3

In the graphical approach to linear programming, finding values for the decision variables at the intersection of corners requires the solving of:

Simultaneous Equations

A redundant constraint is one that:

Does not form a unique boundary of the feasible solution space.

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound.

 

What is the objective function?

$2A + $1B = Z

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

What is the Columbia bean constraint?

12A + 8B ≤ 4,800

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

What is the Dominican bean constraint?

4A + 8B ≤ 3,200

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

Which of the following is not a feasible production combination?

400 A and 0B

The production planner for Fine Coffees, Inc., produces two coffee blends: American (A) and British (B). Two of his resources are constrained: Columbia beans, of which he can get at most 300 pounds (4,800 ounces) per week; and Dominican beans, of which he can get at most 200 pounds (3,200 ounces) per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. 

 

For the production combination of 0 American and 400 British, which resource is "slack" (not fully used)?

Colombian beans (only) | 4800 > 3200

A novice linear programmer is dealing with a three-decision-variable problem. To compare the attractiveness of various feasible decision-variable combinations, values of the objective function at corners are calculated. This is an example of:

Enumeration

When we use less of a resource than was available, in linear programming that resource would be called non-________.

Binding

Once we go beyond two decision variables, typically the ________ method of linear programming must be used.

Simplex

________ is a means of assessing the impact of changing parameters in a linear programming model.

Sensitivity Analysis

For a linear programming problem with the following constraints, which point is in the feasible solution space assuming this is a maximization problem?

x = 2, y = 1

Which of the following choices constitutes a simultaneous solution to these equations?

x = 2, y = 1

What combination of x and y will provide a maximum for this problem?

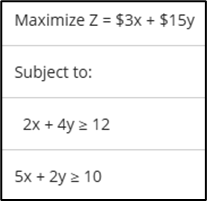
x = 0, y = 5