Sets

‘Definition’, Notation and Exam, Set Relations: Subset and Equality, Set Operations, Some Set Identities, Another Set Operation: Cartesian Product

Set

A set is a collection of distinct objects, called elements, denoted by curly brackets {}.

A = {1,2,3,4,5}

Element

An element is an object that belongs to a set, denoted by…

x ∈ A

(x is an element of set A).

Subset

A set A is a subset of set B if every element of A is also an element of B, denoted A ⊆ B.

If A ⊆ B and A ≠ B, then A is a proper subset of B - A ⊂ B

All sets are also subsets of themselves! And the empty set is a subset of all sets!

Natural Numbers

The set of positive integers denoted as N.

N = {1, 2, 3, 4, . . .}

Integers

The set of all integers, including positive, negative, and zero, denoted as Z.

Z = {. . . , −3, −2, −1, 0, 1, 2, 3, . . . }

Rational Numbers

The set of numbers that can be expressed as a fraction n/m where n, m ∈ Z and m ≠ 0, denoted as Q

Q = { m/n : m,n ∈ Z and n ≠ 0}

Real Numbers

The set of numbers that can be expressed with an infinite decimal expansion, denoted as R.

Complex Numbers

The set of numbers expressed in the form a + bi where a, b ∈ R and i is the imaginary unit, denoted as C.

Empty set

A set with no elements in it is called an empty set, denoted by ∅.

∅ = {}

Intervals

[ = greater than equal to

] = less than equal to

{ = greater than

} = less than

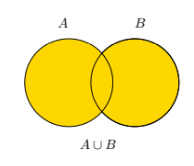
Union

The set of all elements that are in either set A or set B, denoted A ∪ B.

Intersection

The set of all elements that are in both set A and set B, denoted A ∩ B.

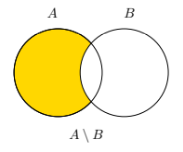
Set Difference

The set of elements that are in set A but not in set B, denoted A \ B.

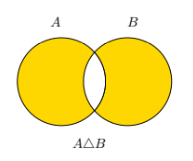
Symmetric Difference

The set of elements that are in either set A or set B but not in both, denoted A △ B.

Complement

The set of all elements in a universal set that are not in set A, denoted A^c.

Cartesian Product

A and B are sets, the Cartesian product of A and B is the set of all ordered pairs (a, b) with a ∈ A and b ∈ B. We denote this by A×B so

A × B = {(a, b) : a ∈ A and b ∈ B}

{1, 2} × {1, 2, 3} = {(1, 1),(1, 2),(1, 3),(2, 1),(2, 2),(2, 3)}
{1, 2, 3} × {1, 2} = {(1, 1),(1, 2),(2, 1),(2, 2),(3, 1),(3, 2)}