Linear motion and SUVAT equations

when can SUVAT equations be used?

SUVAT equations are used when there is constant acceleration

thinking distance

Distance travelled between when the driver sees a problem and the time at which the brakes are applied. 

Thinking distance = speed x reaction time

Where reaction time is dependent on tiredness, alcohol or drug use, illness and distractions.

reaction time

the time it takes for a person to react to a stimulus (e.g. the time it takes a driver to observe an obstacle and apply the brakes).

the time taken between a driver seeing a problem and reacting to the problem (i.e. applying the brakes)

A car is travelling at a constant speed towards an obstacle. What is the relationship between reaction time and thinking distance?

The smaller the reaction time, the smaller the thinking distance

braking distance

the distance travelled by the vehicle from when the brakes are first applied to when the vehicle has come to a complete stop.It is affected by the road conditions and the quality/wear of the tyres

A cyclist has just started applying the brakes to her bike. The brakes continue to be applied for a total of 5 s until the bike has come to rest. The average speed during this time is 2 m s−1. Calculate the braking distance.

The question tells us that the cyclists travels an average speed of 2 metres per second for 5 seconds. It follows that they will travel (2 × 5) = 10 m in this time.
∙  ∙ Using our equation for braking distance: Braking distance = (time period when the brakes are applied)×(average speed of bike
∙  ∙ Substituting in the values from the question gives: braking distance=5×2=10m

The tiredness of a driver affects the….

thinking distance

The road condition affects the…

braking distance

braking distance+thinking distance=

stopping distance

A tractor has the following speed-time graph:

Calculate the braking distance

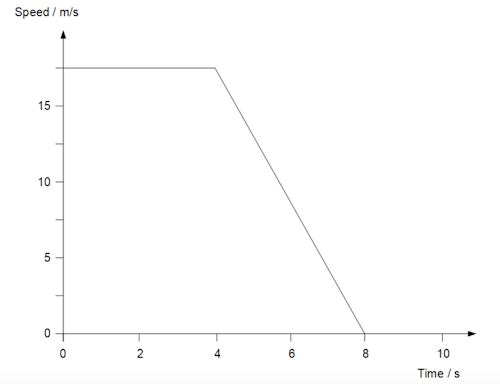
35m

This experiment involves dropping a ball and measuring the time it takes to fall through a set distance. The setup for this experiment is shown in the diagram below.

The time taken for the ball to fall through what distance will be measured using this experiment??

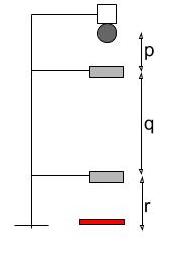
q

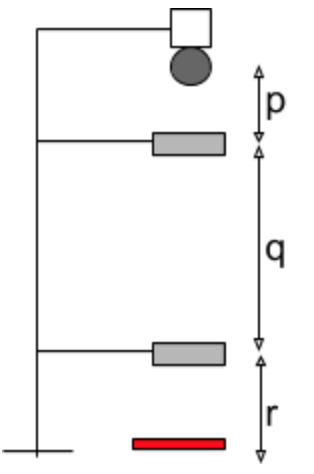
A student times how long it takes a ball to fall through distance ‘q’ after dropping it from different initial heights. If the time ‘t’ is plotted on the x-axis, what quantity should they plot on the y-axis to get ⁡g as the gradient??

If the ball falls distance ‘q’ in time ‘t’ and the acceleration due to gravity is a=g⁡a = g, the equation of motion s=u⁢t+1/2at² becomes q=u⁢t+1/2g⁡t² where ‘u’ is the initial speed of the ball when it falls through the first hatch.
∙  ∙ We want to rearrange this equation into the form y = mx + c, where ‘mm’ is the gradient of the graph and ‘c’ is the y-intercept.
∙  ∙ In this experiment, we want the gradient to be the acceleration due to gravity, so m = g.
∙  ∙ If we plot the independent variable tt on the x-axis, then we want the term ‘mx’ to be ‘gt’.
∙  ∙ This means that we must rearrange q = ut +1/2​ gt2 into the form y = gt + c.
∙  ∙ Doubling both sides and dividing by t gives 2⁢q/t=2⁢u+g⁡t².
∙  ∙ This is of the form y=g⁡t+c where y=2⁢q/t​

Which of the following is a safety precaution that is used in this experiment??

This experiments uses electromagnets, so there is a potential risk of electrocution. To minimise any damage, use low currents and do not expose yourself to unnecessary risk (e.g. don’t stick your fingers into the power sockets).
∙  ∙ The falling object will bounce off the work surface after it has completed its fall, which may damage the surface. To stop this, use a small cushion or another object to shield the fall.
∙  ∙ Since the stand has several objects attached to it, it may wobble and fall. As well as being a safety hazard, these wobbles will distort the experiment’s results, so they should be minimised by clamping the stand to the desk.

Stopping Distance

The distance travelled from the driver seeing a problem to the vehicle coming to a complete stop. 

Stopping distance = Thinking distance + Braking distance

A young girl is trying to convince her older brother that a ball thrown on Earth vertically upwards will momentarily stop at the top of its trajectory before it falls back to his hand. He finally understands and agrees. Which of the following are also true?

Assume there is no air resistance and that there is zero horizontal displacement.(4)

The initial speed that the ball leaves the hand will equal the final speed of the ball as the thrower receives it.

The time taken to the top of the trajectory is equal to the time taken between the top of the trajectory and the thrower catching the ball.

The acceleration is constant throughout the whole flight of the ball

The distance traveled upward is equal to the distance traveled downwards