Unit 6 - Sampling distributions

Parameter vs. statistic

• Population = numerical descriptive measure of a population

• Statistic = numerical descriptive measure of a sample

Parameters of population vs. statistics of sample

• Parameters

  • \mu = mean

  • \sigma = standard deviation

  • p = proportion

• Statistics

  • x̄ = mean

  • s = standard deviation

  • p̂ = proportion

What is the sampling distribution

• The sampling distribution of a statistic is the distribution of values taken by the statistic in all possible samples of the same size from the sample population

• The idea: take many samples from the sample population, collect the means from all the samples, display the distribution of means on a graph; the histogram will be bell-shaped, symmetric, centered at the population mean; it will be approx. normal

Does sampling distribution or population have larger spread

Sampling distribution always has lower spread bc standard deviation is lower

Variability of a statistic

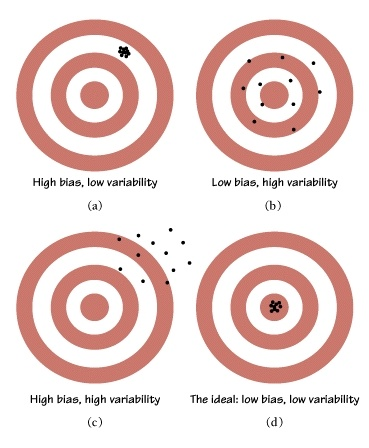
3 conditions to check for sampling distributions

• 1. Normality (shape)

  • If population is approx normal, then sampling distribution is too

  • If population isn’t normal → Central Limit Theorem

    • If sample size is large (n ≥ 30), the sampling distribution is approx. normal

  • Or, use a normal probability plot and check if it’s linear

• 2. Unbiased

  • Check if it’s an random sample

  • If so, μ = μ_x

  • If it’s not obvious, say “verify a random sample was taken”

• 3. Independent

  • Independent if population ≥ 10n (sample size)

  • σ_x = σ/√n

Z score of sampling distribution

z = (x̄ - μ) / σ_x

z_x = (x̄ - μ_x) / σ/√n

Conditions for proportions / variables

• Unbiased - random sample

• Independence - population ≥ 10n

• Normality:

  • np ≥ 10

  • n(1-p) ≥ 10

μp̂ = p

σp̂ = √p(1-p)/n

z = (p̂ - μp̂) / σp̂ = (p̂ - p) / σp̂

Note:

p = true value; use for np ≥ 10, n(1-p) ≥ 10
p̂ = sample; only use for z-score