Computer Graphics Final

ray tracing

rendering model that uses rays emitted by scene objects to identify visibility, lighting, and shading

pipeline rendering

an object-oriented approach to rendering that iterates through scene objects and calculates the shading of each

bayer filter

filters RGB to identify how much light passes through some section of a scene

gamma correction

adjusting stored pixel values to account for display intensity differences

ray tracing PROS

intuitive for visibility

allows for easy shading, refraction/reflection, multiple light sources, etc.

realistic

ray tracing CONS

slow

not good for some complex reflections/lighting effects

1. compute ray through current pixel

2. check for intersection

3. trace shadow rays to all lights

4. compute illumination/shading

5. if reflective, trace reflection ray

6. if transparent, trace transmission/refraction ray

7. combine into pixel value

8. repeat

ray tracing algorithm

specular light

reflected light that produces the highlights we see on shiny objects

diffuse light

light scattered uniformly in all directions —> preserves surface color

independent

diffuse light is view ___

dependent

specular light is view ___

ray equation

r(t) = p_r + td_r

plane equation

p \dot n = d

solving for t in ray-plane intersection

t = (d - p_r \dot n) / (d_r \dot n)

sphere equation

|| p - O ||² - r² = 0

solving for t in ray-triangle intersection

t = ( (a-p) \dot n ) / (d \dot n)

where a is any point on plane

Algorithm for using barycentric coordinates in ray-triangle intersection

1. Compute u and v

   • u = b - a

   • v = c - a

2. Set up the initial matrix

   • [ u v -d_r ] [beta \\ gamma \\ alpha] = [p_r - a]

   • calculate the determinant (DET) of the first matrix above

3. Use Cramer’s rule to solve for beta, gamma

   • gamma = det(u, p_r - a, -d_r) / DET

   • beta = det(p_r - a, v, -d_r) / DET

   • t = det(u, v, p_r - a) / DET

radiant energy (Q)

energy of electromagnetic radiation

radiant flux/power

radiant energy per unit time

irradiance (E)

radiant flux received by a surface per unit area

E = P/4pir²

irradiance for a sphere

inversely, distance, angle of incidence, cosine

irradiance is…

• ____ proportional to square of ___

• affected by ____ as demonstrated by the ___ rule

radiance (L)

radiant flux emitted, reflected, transmitted, or received by a surface, per unit solid angle per unit projected area

I = P/4pi

radiant intensity

E = I cos theta / r²

irradiance from a point light

L_d = k_dE

how to compute diffuse shading with irradiance

L_s = k_sE max(0, cos alpha)^p

how to compute specular shading with irradiance

L_a = k_aI_a

how to compute ambient light shading with radiant intensity

away, background, greater, 0, 1, || l - P ||

when tracing shadows…

• start the ray slightly ___ from the surface to avoid spots

• if the point light is not visible, return ___ color

• start tmin slightly ___ than ___

• if the shadow ray is normalized, set tmax to ___

• else set tmax to __

• increasing samples

• random sampling

• jittered samples

• adaptive sampling

methods for anti-aliasing

random sampling

sampling at non-uniform places in a pixel to reduce aliasing

jittered samples

diving the pixel into a grid and sampling random spots within the grid cells

same, opposite

when a ray intersects with a reflective surface, we compute reflection ray at the ___ angle in the ___ direction

dielectrics

materials that do not conduct electricity (e.g. glass)

snell’s law

describes how light bends as it moves through mediums (e.g. air to glass)

fresnel equations; use the cosine rules to convert snell’s law and solve for cos phi. if the value under the square root is negative, there is total internal reflection

how to determine total internal reflection

R(theta) = R₀ + (1 - R₀)(1 - cos theta)⁵ with R₀ = ((n_t - n)/(n_t + n))²

schlick approximation

schlick approximation

determines how much light is reflected

Beer’s law

shows exponential decay in light intensity through a medium

I(s) = I₀a^s

Beer’s law

manifold tri-mesh

a mesh where every edge is shared by exactly 2 triangles and can be laid flat

manifold tri-mesh with boundaries

a mesh where every edge is used by either one or two triangles and every vertex connects to a single-edge connected set of triangles (e.g. all triangles are connected)

counter-clockwise

how triangles should be oriented

indexed triangle set

stores each triangle once; uses vertex and position arrays to store vertices and coordinates, respectively t

triangle strips

created by reusing the 2nd and 3rd vertices when defining a new triangle

triangle fan

created by using the first triangle vertex as the origin for all new triangles

triangle neighbor structure

extension of triangle set; uses a triangle object to point to 3 neighboring vertices and a vertex object to point to a neighboring triangle

1. create empty mesh object

2. add mesh vertices

3. add mesh faces

process for building an OpenMesh cylinder

1. mesh→request_face_normals()

2. for each face

   1. create new FaceNormal object face_normal

   2. mesh→set_normal(*fit, face_normal)

process for computing face normals

quick rejection

if a ray does not hit within a bound, move on. else, check if it has an object

axis-aligned bounding boxes

boxes aligned with x, y, z coordinates, framing objects

uniform spatial subdivision

using grids to break down a scene; if cells are empty, we do not check for ray-intersection

1. allocate a grid as a single block of pointers with one for each cell

2. if a cell is empty, pointer = 0

3. if a cell has objects in it, point to a list of the objects

uniform grid set-up

mailboxing

storing a ray hit into a different cell with the ray id for later consideration

BVH trees

hierarchical bounding boxes

KD trees

similar to BVH tree, but driven by heuristics

binary space partitioning trees

allows your to determine visibility ordering of scene objects without changing the viewpoint by using non-axis-aligned splitting planes

1. modeling: object space → world space

2. camera: world space → camera space

   1. vertex shading

3. projection: camera space → canonical view volume

   1. clipping

4. screen space

5. rasterization / z-buffer

6. fragment shading

transformations in the graphics pipeline

focal length

distance between the eye and view plane

far plane

bounds the max distance that an object can be seen from the eye

world space → camera space

vertex shading is performed at the ___ transformation

M_vpM_orthPM_camM_mod

matrix transformations in the graphics pipeline from world to screen space

Gouraud shading

computing the shading at each pixel during rasterization, then linearly interpolating the colors of the remaining pixelsp

phong shading

shading each pixel and then interpolating the vertex normals

camera space → projection space

clipping occurs in the ___ stage

clipping

process by which primitives outside the camera are either discarded or altered

• glossy reflections

• translucency

• depth of field

• motion blue

• soft shadows

• global illumination

monte carlo ray tracing allows for the implementation of…

monte carlo ray tracing

sends multiple rays over some distribution and takes their intersections

depth of field

the distance between the nearest and farthest objects in focus

1. Sample area light by sending shadow rays to random points on light

2. Scale shadow ray contribution by cos theta, where theta is the angle between the surface normal and direction to specific light sample.

3. Scale each sample by 1/d² where d is the distance to the sample and cos alpha, where alpha is the angle between the light’s normal and the direction towards the point on light

4. Scale energy contribution of each shadow ray by area of light source

steps to compute light from area light

bidirectional reflection distribution function (BRDF)

reflectance as a function of viewer and light source directions with respect to normal; shows how much light goes in each direction as it leaves a surface

vertex buffer object

located on GPU; stores vertex attributes (e.g. position, color)

vertex array object

stores VBOs

homogeneous coordinates

adding another dimension to the matrix to combine the translation with the other linear transformations

if the pixel’s center is inside the triangle, draw it. if the center is right on the edge of the triangle, choose an off-screen point to discriminate. draw the pixel for the triangle where the off-screen point is on the same side as the triangle

process for rasterizing triangles

y’ = focal_length / distance_from_eye_to_obj * y

how to compute the height of an object on the view plane

projective transformation to far plane

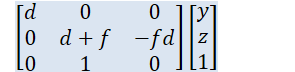
projective transformation to view plane

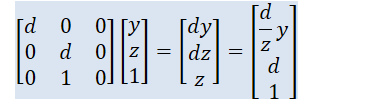
viewport transformation matrix

transforms an object from a canonical view volume to the screen; maps image properly to screen dimensions

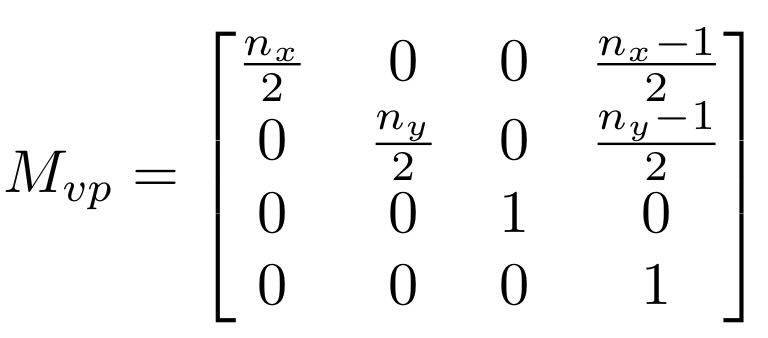
camera transformation

moves camera from position in world space to a convenient location and orientation. also transforms other elements to match.

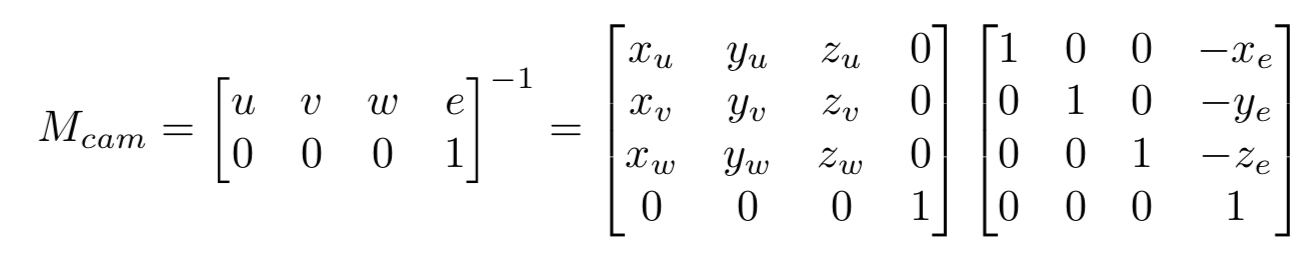
orthographic view transformation

transforms points from orthographic view volume (e.g. AABB) to canonical view volume; ensures all visible points fit in desired range

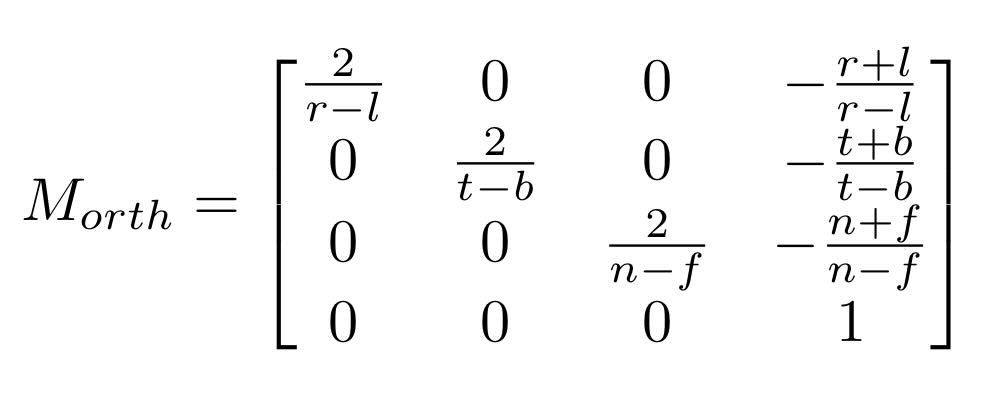
flat shading

each mesh face has 1 normal, creating a blocky appearance

smooth shading

mesh faces’ vertex normals are interpolated, making the mesh appear smooth

vertex shading

occurs in world to camera transformation; process of performing the lighting calculation at a point in the scene (usually vertex) and then (later) linearly interpolating them

fragment shading

occurs after rasterization; computes shading by using interpolated vectors to avoid the interpolation of vertices; enables texture mapping

culling

identifying and throwing away invisible geometry to minimize processing time