Further mechanics

ALEVEL PHYSICS

What is uniform circular motion?

motion of an object rotating at a steady rate.

The object moves in a circular path at a constant speed

velocity is continually changing because its direction is changing

Define angular displacement (θ) and angular speed (ω)

Angular displacement (θ) is the angle an object in circular motion turns through, radians (rad).

Angular speed (ω) is the angular displacement per second. radians per second (rad s⁻¹)

What are the key equations for an object in uniform circular motion?

Speed (v): v = 2πr / T

Relationship between linear and angular speed: v = ωr

Centripetal acceleration (a): a = v²/r = ω²r

Centripetal force (F): F = mv²/r = mω²r

What is centripetal acceleration and in which direction does it act?

the acceleration of an object moving in a circle at a constant speed

caused by the continuous change in the direction of its velocity.

The acceleration is always directed towards the centre of the circle

What is centripetal force and what provides it?

the resultant force required to make an object move in a circular path.

acts towards the centre of the circle, in the same direction as the centripetal acceleration.

provides the:

    ◦ Tension in a string for a whirling object.

    ◦ Gravity for a satellite orbiting a planet.

    ◦ Sideways frictional force between tyres and the road for a car on a roundabout

Define oscillation

The motion of an object moving repeatedly one way and then in the opposite direction through its equilibrium position

What is phase difference between two oscillating objects?

the fraction of a cycle between the vibrations of two objects oscillating at the same frequency.

degrees or radians.

Formula: Phase difference (radians) = 2π (Δt / T)

What is the defining condition for Simple Harmonic Motion (SHM)

The acceleration is directly proportional to the displacement from the equilibrium position

always directed towards the equilibrium position.

a proportional -x

How do displacement vary with time in SHM?

Varies as a cosine or sine wave. If starting at maximum displacement (+A) at t=0, x = A cos(ωt)

How do velocity vary with time in SHM?

Is the gradient of the displacement-time graph. It is maximum at x=0 and zero at x=±A.

The velocity leads the displacement by 90° (π/2 radians)

How do acceleration vary with time in SHM?

Is the gradient of the velocity-time graph. It is maximum at x=±A and zero at x=0.

The acceleration is 180° (π radians) out of phase with the displacement

What are the key equations for SHM systems?

Velocity (v): v = ±ω√(A² - x²)

• Maximum speed (v_max): v_max = ωA (occurs at x=0).

• Maximum acceleration (a_max): a_max = ω²A (occurs at x=±A).

• Mass-spring system period (T): T = 2π√(m/k).

• Simple pendulum period (T): T = 2π√(L/g)

How do kinetic and potential energy vary during SHM?

Total energy (E_total): Remains constant in an undamped system. E_total = ½kA² = ½mω²A².

Potential energy (E_p): Is maximum at maximum displacement (x=±A) and zero at equilibrium (x=0). E_p = ½kx².

Kinetic energy (E_k): Is maximum at equilibrium (x=0) and zero at maximum displacement (x=±A). E_k = ½k(A² - x²).

What is damping and what are the three types?

Damping is the process where resistive forces (like friction or air resistance) cause the amplitude of oscillations to decrease over time.

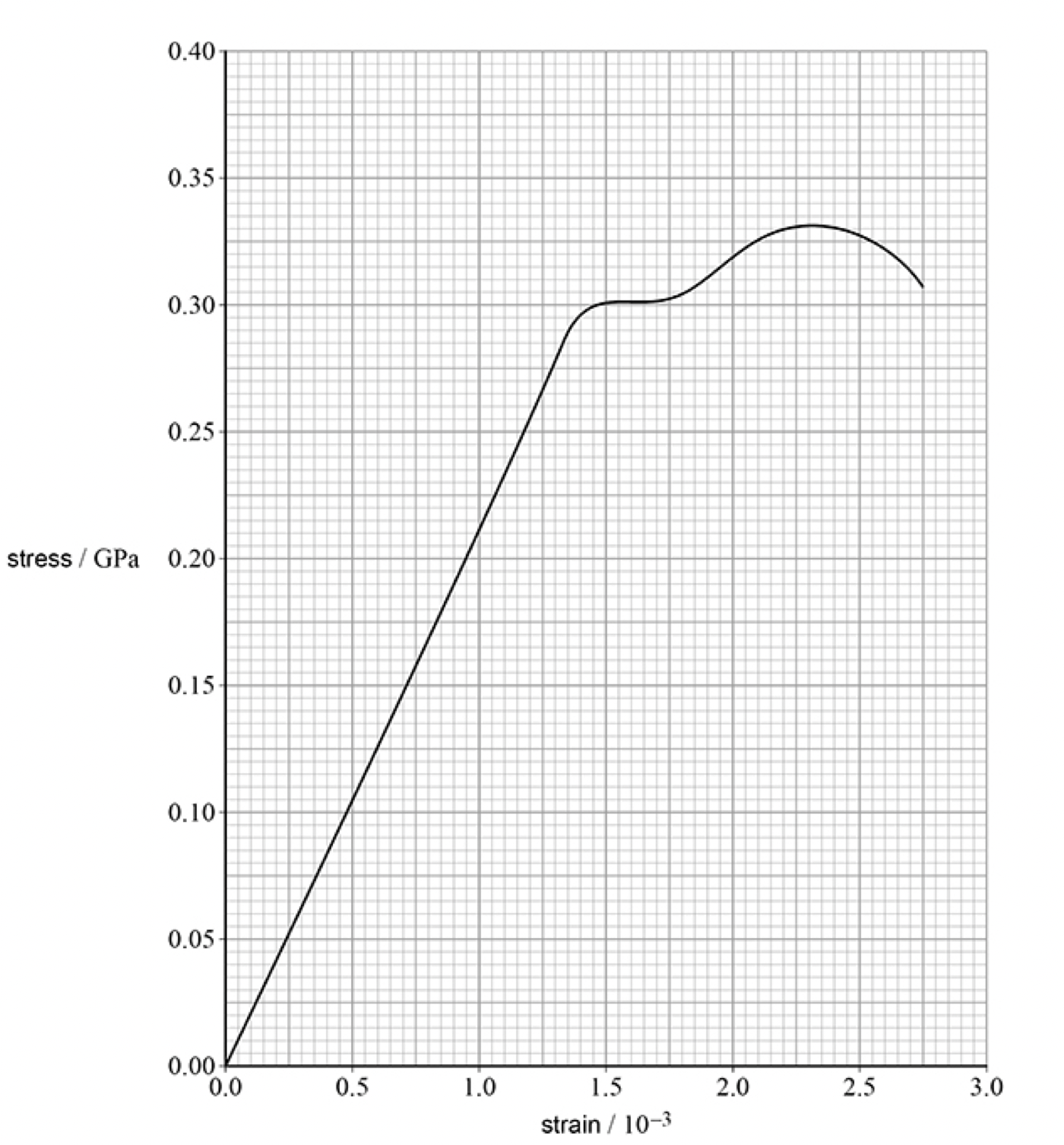
    1. Light damping: Amplitude decreases gradually, with the time period remaining constant.

    2. Critical damping: The system returns to equilibrium in the shortest possible time without oscillating.

    3. Heavy damping: The system returns to equilibrium much more slowly than with critical damping, and does not oscillat

What are forced vibrations and resonance?

Forced vibrations occur when a periodic driving force is applied to an oscillating system.

Resonance occurs when the applied frequency of the periodic force matches the natural frequency of the system, causing the amplitude of the oscillations to reach a maximum.

is 90° (π/2 radians) out of phase with the displacement and in phase with the velocity, leading to maximum energy transfer.

Lighter damping results in a larger amplitude at resonance and a sharper resonance curve

Block constantly changing direction (at constant speed)

Changing direction shows (centripetal) acceleration

Centripetal force acts inwards / towards the centre of rotation

Links reaction force to centripetal force

In this spacecraft mA < mB.

Deduce whether the centre of mass of A or the centre of mass of B rotates with a greater linear speed.

The angular speed is the same for A & B

v = rω so velocity of A is greater.

The astronauts live in A and the cargo is stored in B.

When loaded,

mA = 1.32 × 106 kg

mB = 3.30 × 106 kg.

The spacecraft imitates the gravity of Mars where g = 3.7 m s−2

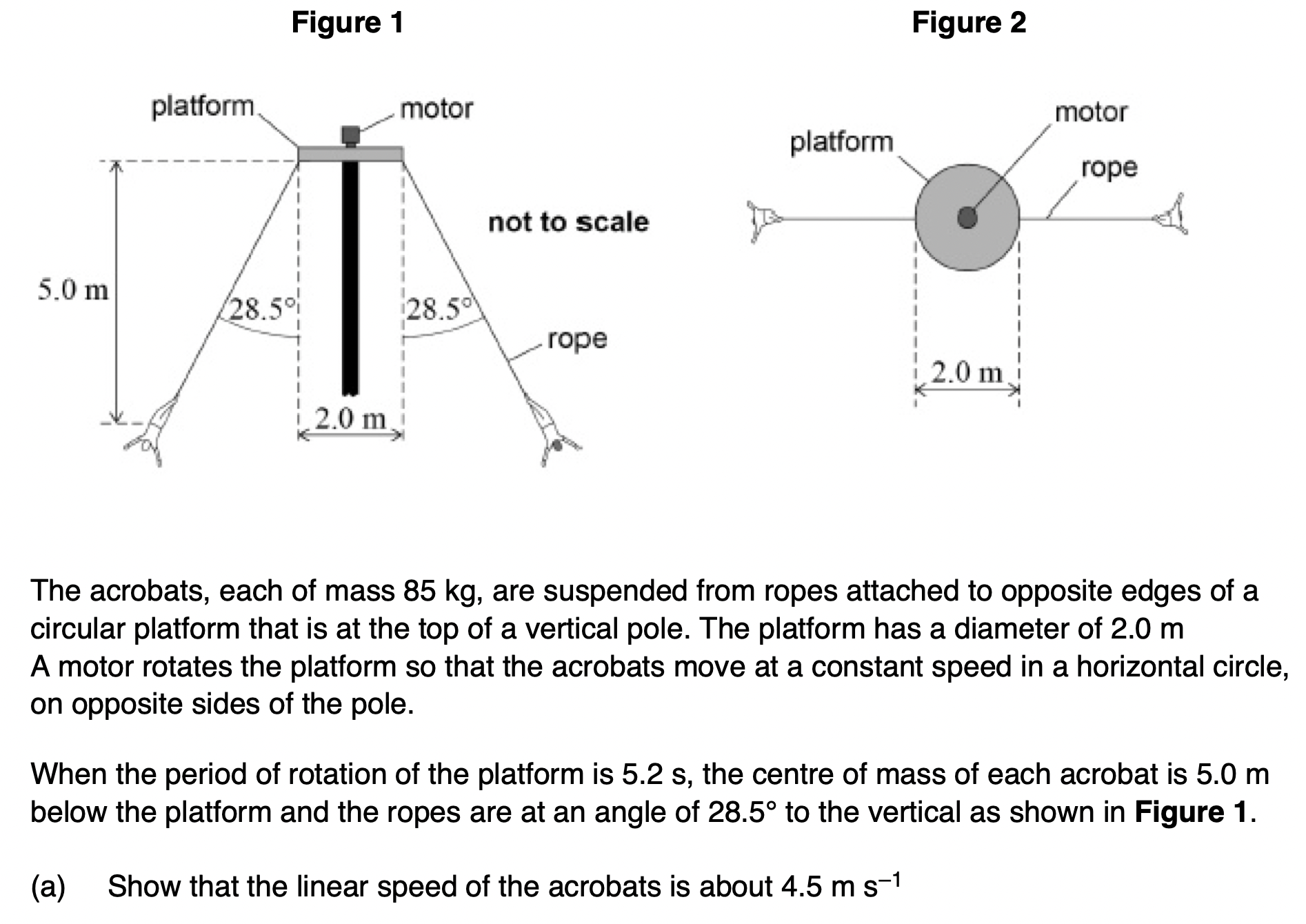
Discuss the consequences for the forces acting on the pole when one acrobat has a much greater mass than the other.

Vertical (compressive) force on the pole increases

Increases mass increases weight and hence tension in the rope

Centripetal Force; on the acrobats masses would be different

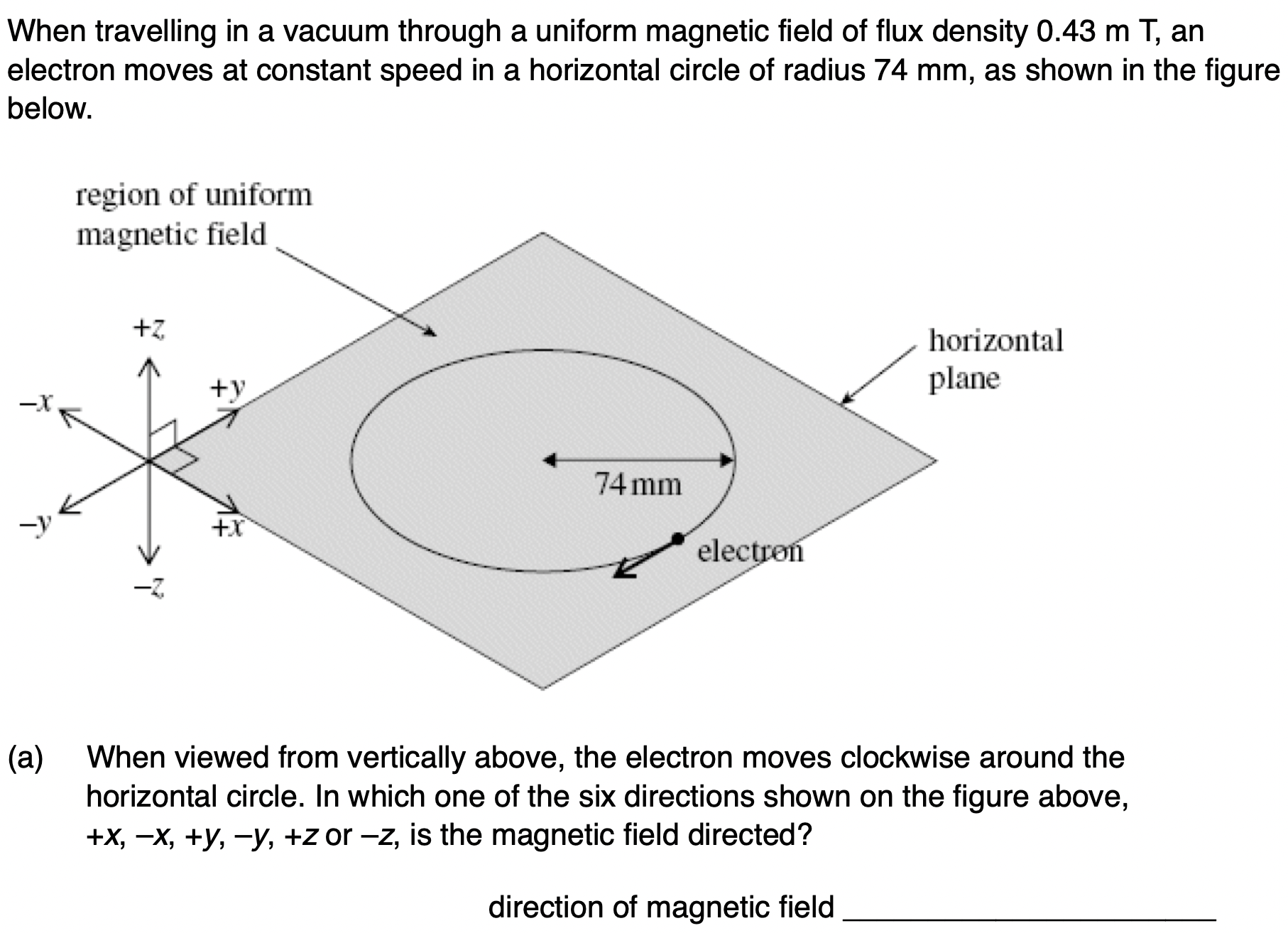
magnetic field direction: −z

Explain why the electron is accelerating even though it is travelling at constant speed.

direction changes meaning that velocity is not constant

acceleration is rate of change of velocity