CH 2 - sequential Experiments

Tree Diagrams

Display outcomes of subexperiments in sequential experiments. Branch labels = probabilities/conditional probabilities. Probability of full outcome = product of branch probabilities.

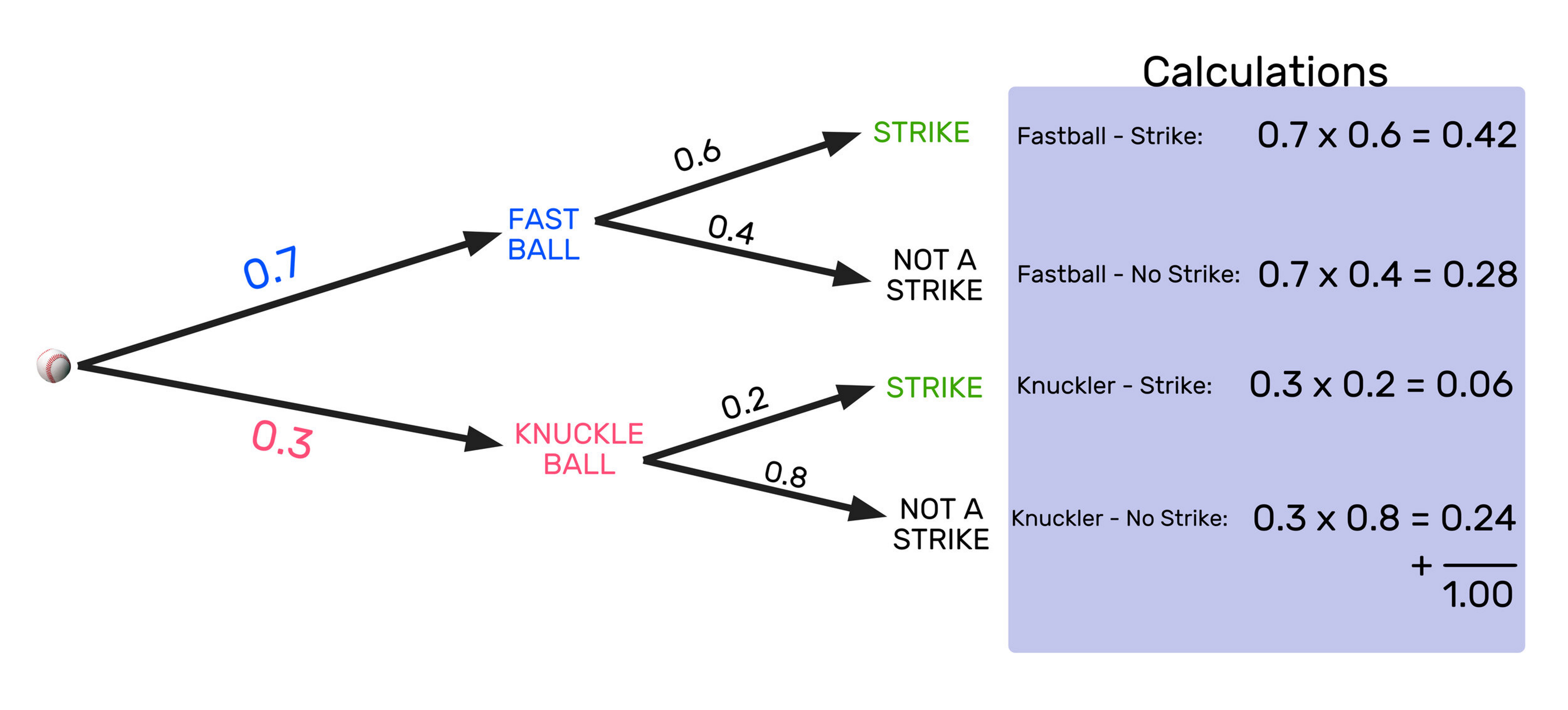
Probability of leaf in tree

Multiply probabilities along branches from root to leaf.

Counting Methods

Finding number of possible outcomes without listing them. ( Permutations, Combinations)

Multiplication Rule

Total outcomes = (outcomes of first) × (outcomes of second).

Permutation with Replacement

Order matters, replacement allowed. Formula: m^k.

Permutation without Replacement

Order matters, no replacement. npr on calculator

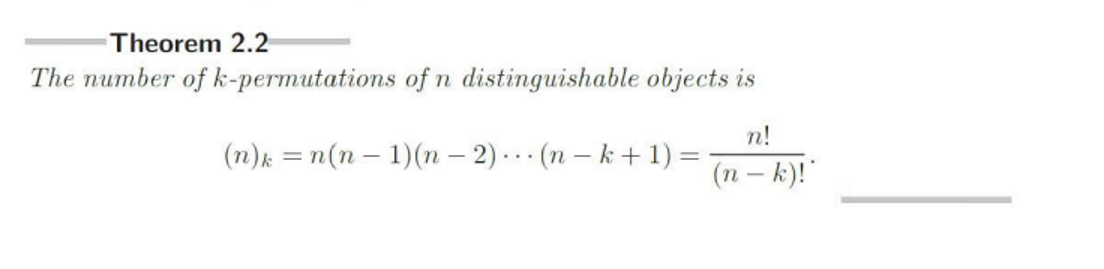
Combination without Replacement

Order does not matter, no replacement. NCR on calculator

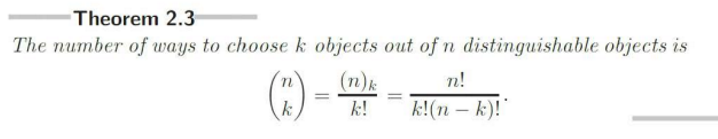
Combination with Replacement

Order does not matter, replacement allowed. Rarely used.

(n)k

Number of k-permutations of n distinguishable objects = n! / (n-k)!.

Sampling with Replacement

Leads to independent trials.

Independent Trials

Outcome of one trial does not affect probabilities of next (e.g., coin flips, dice rolls).

Binary Trials

Trials with two outcomes (success/failure). Sample space = {0,1} or {S,F}.

Binomial Probability

If n trials and success probability = p, probability of k successes: (n choose k) * p^k * (1-p)^(n-k).