DISCRETE MATH CHAPTER 3 REVIEW

Relations

can be used to store information in the computer databases. Relationships between people, numbers, events, letters, sets, and many other entities can be formalized in the idea of a binary relation. It is a binary relation because it relates two objects.

1. two ordered pair

2. binary relation.

3. left component

4. right component

If 1._________ of elements are written, separated by comma and enclosed by parentheses like (a, b), they form a 2. __________ In a binary relation (a, b), a-coordinate as called the 3.__________ or the domain and the b-coordinate is called the 4. _________ or the range.

• If yung element ng (a, b) ay element ∈ ng R we write aRb and say that a is related to b

• while a/Rb means “a is not related to b” or (a, b) ∉ R

• For Example: R = {(1,2),(2,5),(6,6)}

  then

  1R2 , one is related to 2

  2/R6 , two is not related to 6

1. DOMAIN

2. RANGE

The 1. _________of R (denoted by D(small) R (DR) is the set of all left components of the elements of R.

• DR = { a ∈ A | (a, b) ∈ R for some b ∈

• B } = { a | aRb}

The 2. _________ of R (denoted by R(small) R (RR0 is the set of all right components of the elements of R.

• RR = { b ∈ B | (a, b) ∈ R for some a ∈

• A } = { b | aRb}

  DR ⊆ A and RR ⊆ B.

  • Domain is a subset of A, and Range is a subset of B

  If A = B, then we call R a relation on A.
  
  

So given na ang A, B, at R

ang gagawin nalang ay i arange so,

DR = {1, 2, 3}

RR = {a, b}

Ordered pairs

Methods of Describing Relations

R = {(1, x), (2, y), (3, z), (4, w)}

Rule Form

Methods of Describing Relations

R = {(a, b) | b = a2}

R = {(a, b) | b < a + 2}

Arrow Diagrams

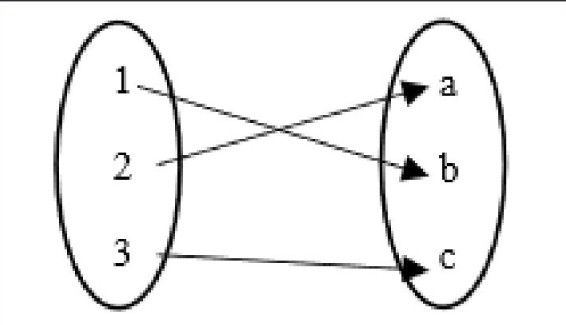
Methods of Describing Relations

A = {1,2,3}

B= {a,b,c}

R = {(1,b),(2,a),(3,c)}

Tables

Methods of Describing Relations

Rectangular Array (or Matrix)

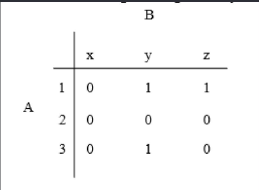
Methods of Describing Relations

A = {1,2,3}

B = {x,y,z}

R = {(1,y),(1,z),(3,y)}

so sabe A x A so multiply by itself lang so,
A = {1, 2, 3, 4} and A = {1, 2, 3, 4} ,, R = {(a, b)

a divides b, since a ang b naten divide by its self lang

A x A = {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}

now divide,, 1 can be divided from 1-4, 2 can be divided by 2 or 4, then 3 and 4 by themselfes

R = {(1,1),(1,2),(1,3),(1,4),(2,2),(2,4),(3,3),(4,4)}

IDENTITY RELATIONS

Let A be a set. The identity relation on A is denoted by IA, and is given by the symbols :

▪ IA = {(a, a) | a ∈ A}.

IVERSE RELATIONS

Let R be a relation from A to B. The inverse of R, denoted by R-1, is the relation from B to A given by bR-1a if and only if aRb, in symbols

if R-1 naman, ang domain nya ay ang range ng R (pagbabaliktadin lang)

So, we solve for INVERSE relation of R

if R = {(1, 2), (2, 3), (3, 4), (4, 1)}. babaliktadin lang ang D at R
so, R-1 = {(2, 1), (3, 2), (4, 3), (1, 4)}

next is IDENTITY RELATION

if A = {1, 2, 3, 4} i copy lang to itself

so, IA = {(1, 1), (2, 2), (3, 3), (4, 4)}

GIVEN:

A = {1, 2, 3} and B = {a, b, c}. and R = {(1, a), (2, b), (3, c)}

INVERSE RELATION (pag baliktadin)

R-1 = {(a, 1), (b, 2), (c, 3)}

IDENTITY RELATIONS OF A (copy by itself)

IA = {(1, 1), (2, 2), (3, 3)}

IDENTITY RELATIONS OF B (copy by itself)

IB = {(a, a), (b, b), (c, c)}

Composition of Relations

(RoS)

Let R be a relation from A to B and S be a relation from B to C. The composition of R and S Denoted by RoS, is the relation from A to C defined by:

R o S = {(a, c) | (a, b) ∈ R and (b, c) ∈ S for some a ∈ A, b ∈ B, c ∈ C}

Note: The composition of relations R and S is commonly written as R∘S. However, some texts use S∘R to align with function composition notation (like g∘f).

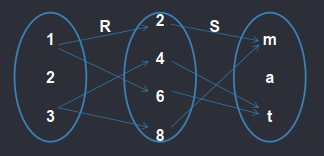
So ang composition of relations kase, visually i mamatch mo muna yung R to o then o to S

So Bale

mag cross muna sa path, then tawid papuntang S

1. Suppose:

A = {1, 2, 3} ; B = {2, 4, 6, 8}; C = {m, a, t}

Let (Defined) (Given)

▪ R = {(1, 2), (1, 6), (3, 4), (3, 8)} be a relation from

set A to set B; and

▪ S = {(2, m), (4, t), (6, t), (8, m)} be a relation from

set B to set C.

• R2={(1,2),(1,3),(2,2),(3,3)}

• R3={(1,2),(1,3),(2,2),(3,3)}

wi

Digraph of Relations

1. ___________ of Relations It consist of a circle and an arrow which can be draw like the arrow diagram. The only difference is that every circle of the digraph contain one element.

EXAMPLE

Draw the digraph determined by the relation below.

R={(1,1),(1,2),(1,3),(2,3),(3,3),(4,2),(4,3),(4,4) }

Matrix of Relations

A ____________ is a way to represent a binary relation between two finite sets using a matrix (a grid or table) filled with 0s and 1s.

Draw the matrix determined by the relation below.

R={(1,1),(1,3),(2,2),(2,3),(2,4),(3,3),(4,4)}

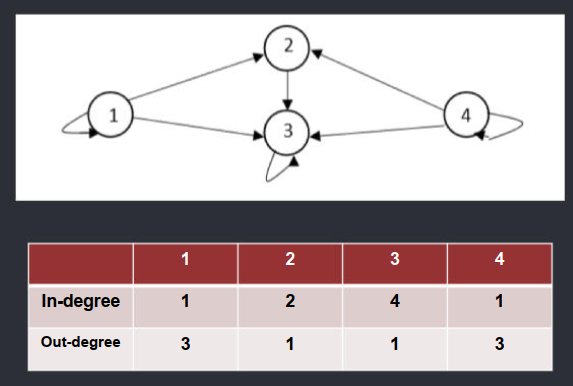
Let A = {1,2,3,4}; R = {(1,2), (2,2), (2,4), (3,2), (3,4), (4,1), (4,3)}. Given the relations create a digraph, list of in-degree and out-degree of all vertices in a table, and matrix.

REFLEXIVE

▪ A relation R is ________ if for every a ∈ A, (a, a) ∈ R

should be:

• element a is part of set A

• kumpleto sa relation yung ordered pair

• if set a is 1,2,3 then sa relation ay dapat (1,1) (2,2) (3,3)

SYMMETRIC

• A relation R is _______ if whenever (a, b) ∈ R, then (b, a) ∈ R.

• if existing yung ordered pair na a and b, pag binaliktad mo sya dapat nandyon parin sya
  

  ex: 1,1 pag binaliktad 1,1 paren

• A relation is not _______ if there exists (a, b) ∈ R but (b, a) ∉ R.

  should be:

• if existing yung ordered pair na a and b, pag binaliktad mo sya dapat nandyon parin sya, pero if may isang hindi nagkapareho, then it is not.

  ex: 1,1 , at 1,3 then not sya

ANTISYMMETRIC

• A relation R is __________if whenever (a, b) and (b, a) belong to R then a = b.

EX: (a,b)(b,a) substitute (1,1)(1,1)

dapat yung value ng domain ay equal sa domain ng 2nd pair, also yung value ng range ay dapat equal sa range value ng 2nd pair

• A relation R is not ________ if there exists (a, b) ∈ A such that (a, b) and (b, a) belong to R but a ≠ b.
  

TRANSITIVE

• A relation R on a set A is ________ if whenever (a, b), (b, c) ∈

  R then (a, c) ∈ R.

yung range (b) ng 1st pair ay dapat same value ng domain (a) ng other pair then also dapat mayroong domain (a) ng 1st pair and range (b) ng other pair sa relations

it doesn’t matter kung magkalayo yung pair, as long as mayroong match na range and domain, at mayroong relations na domain and range

dapat ang tatlong ito ay makita sa relations

ex: (1,2),(2,3) then (1,3)

• A relation R is not ________ if there exists (a, b, c) ∈ A such that (a, b), (b, c) ∈ R, but (a, c) ∉ R.