Sequence and Summitation Notation Nation

You can do it!

infinite sequence

a function whose domain is the set of all positive integers

finite sequence

the function consists of only n positive integers

fibonacci sequence

the sequence is definded recursively - the next term is defined by the previous term

series

the sum of a sequence

Partial sum

Contains an ending value

Actual infinite sum

Eventually will approach a number

Finite Arithemtic Sequence

S_n = n/2 * a₁ + a_n (a₁ = first term, a_n = last term)

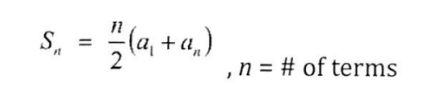
Recursion Formula

If you know the n^th term and the common difference, you can find the (n+1) term by using a_n+1 = a_n + d

Annuity Equation

p * ((1+iⁿ) -1) / i)

a

total amount

P

principle (initial) amount

n

number of payment periods

i

% rate / number of payments each year

Sum of geometric sequence

S_n = a(1-rⁿ / 1-r) where r does not equal 0 or 1

Sum of an Infinite Geometric Series

if |r| < 1 then a/1-r