Matiekos egzas

Funkcijos kitimo greiciu taske x0 arba isvestine

.

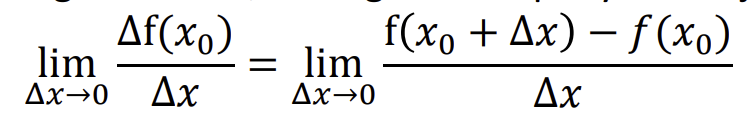
Funkcijos diferencijavimas

Funkcijos isvestines radimas

Funkcijos isvestines uzrasymas

.

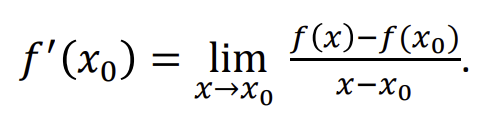
Vienpuse isvestine is kaires

.

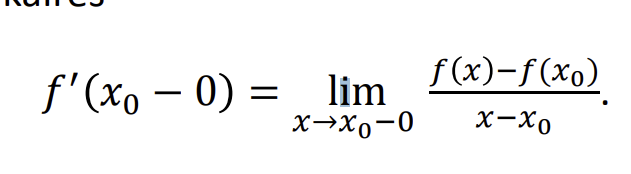
Vienpuse isvestine is desines

.

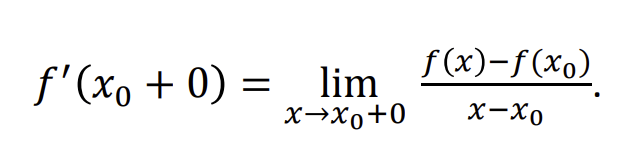
Kreives liestine taske M0

Ribine padetis M0T kuria uzima kirstine M0M kai taskas M arteja prie tasko M0

Krypties koeficiento lygtis

.

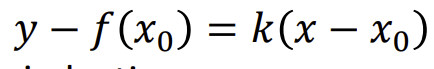
Kreives liestines lygtis

.

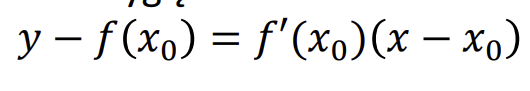
Kreives normale

Tiese einanti per lietimosi taska, yra statmena liestinei

Kreives normales lygtis

.

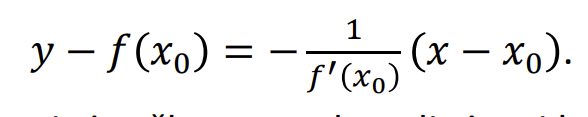
Funkcija siame taske tolydi

Jei funkcija turi isvestine taske x0

Atvirkstines funkcijos diferencijavimas

.

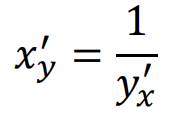
Rolio teorema

Jei funkcijos reiksmes atkarpos galuose lygios, tai egzistuoja bent vienas vidinis atkarpos taskas kuriame funkcijos liestine yra lygiagreti asiai Ox

Kosi teorema

Funkcijos f(x) ir g(x) tolydzios atkarpoje, diferencijuojamos bent intervale (a ; b) tada tarp a ir b yra taskas c

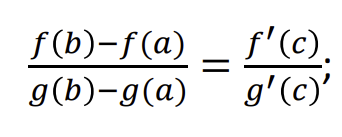
Lagranzo teorema

Jei funkcija tolydi atkarpoje diferencijuojame intervale, tai tarp a ir b yra taskas kuriame f(b) - f(a) = f’( c ) * (b-a)

Liopitalio teorema

.

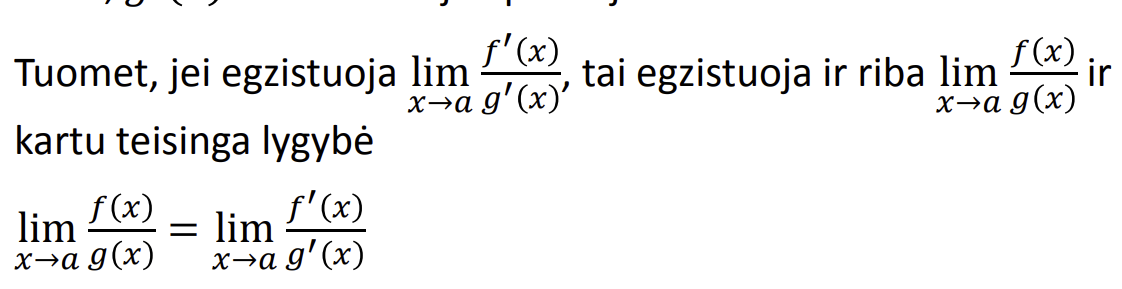
Funkcijos diferencialas

.

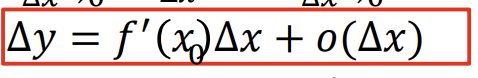
Pastovi funkcija

Jei diferencijuojamos intervale funkcijos isvestine visuose taskuose lygi nuliui tai f(x) tame intervale

Funkciju monotoniskumas

Jei diferencijuojamos intervale funkcijos isvestine teigiama/neigiama tai funkcija tame intervale dideja/mazeja

Funkciju ekstremumai

Maksimumas ir minimumas.

Funkcijos reiksme kai tasko x teisinga nelygybe f(x0) > f(x) arba f(x0) < f(x)

Funkcijos kritiniai taskai

Taskai kuriuose isvestine lygi nuliui arba neegzistuoja

Funkcijos ekstremumo egzistavimo taisykle

Kai f’(x0) = 0 o f’’(x0) < 0/f’’(x0) > 0 tai x0 yra maksimumo/minimumo taskas

Kreives iskilumas

Kreive iskila aukstyn/zemyn intervale jei visi tos kreives taskai yra po liestine/virs liestines

Kreives perlinkio/vingio taskai

Taskas kuris atskiria iskila aukstyn dali nuo iskilos zemyn

Jei f’’(x0) = 0 ir antroji isvestine eidama per taska keicia zenkla tai x0 perlinkio taskas

Kreives iskilumas teorema 1

Jei intervale funkcija turi antraja isvestine kuri neigiama/teigiama tai kreive yra iskila aukstyn/zemyn

Funkcijos grafiko asimptotes

Tiese, jei bet kurio kreives tasko atstumas iki tos tieses arteja prie nulio, taskui tolstant kreive

Vertikaliosios asimptotes

Jei nors viena is ribu yra begaline, tai tiese x = a

Pasvirosios asimptotes

b = lim x → inf (f(x)-kx)

k = lim x → inf f(x) / x

Bendroji tyrimo schema

Nustatome apibrezimo sriti, trukio taskus, funkcijos ribas is kaires ir desines, ribas srities galuose

Istiriam ar funkcija lygine/nelygine, periodine/neperiodine

Issprende f(x) = 0, gauname taskus kuriuose kerta Ox asi

Diferencijuojam funkcija, randam kritinius taskus, nustatom isvestines zenkla visuose intervaluose. Apskaiciuojame ekstremumus

Isdiferencijuojam antra karta, apskaiciuojam antrosios isvestines zenklus tuose intervaluose, suzinom iskilumo aukstyn ir zemyn intervalus, perlinkio taskus

Randame vertikalias ir pasviras asimptotes

Nubraizome grafika

Pirmykstes funkcijos apibrezimas

Jei visuose funkcijos atkarpos taskuose teisinga lygybe F’(x) = f(x) arba dF(x) = f(x)dx

Pirmysktes funkcijos teorema

Jei dvi funkcijos pirmykstes atkarpoje [a,b] tai jos viena nuo kitos skiriasi tik konstanta C

Neapibreztinis integralas

Jei funkcija yra pirmykste funkcija tai reiskinys F(x) + C

Integravimas

Veiksmas, kuriuo randama duotosios funkcijos pirmykste funkcija.

Atvirkstinis diferencijavimui

Pagrindines neapibreztinio integralo savybes

.

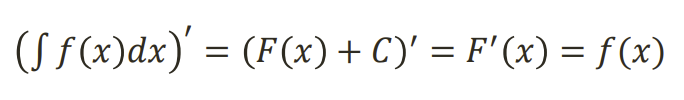
Pagrindines neapibreztinio integralo savybes

.

Pagrindines neapibreztinio integralo savybes

.

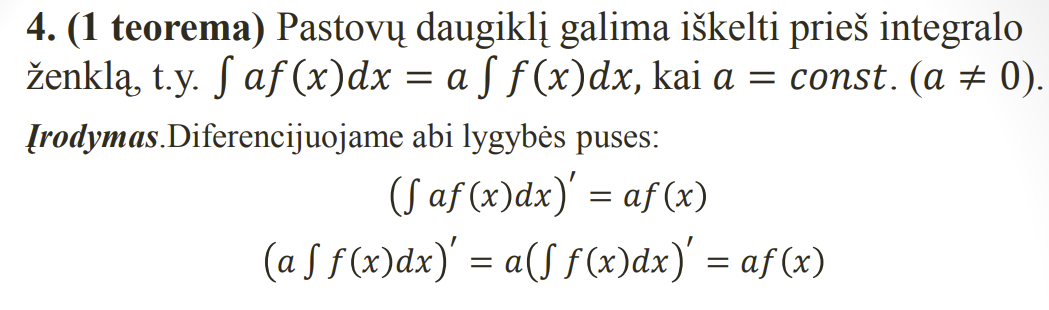
Pagrindines neapibreztinio integralo savybes

.

Pagrindines neapibreztinio integralo savybes

.

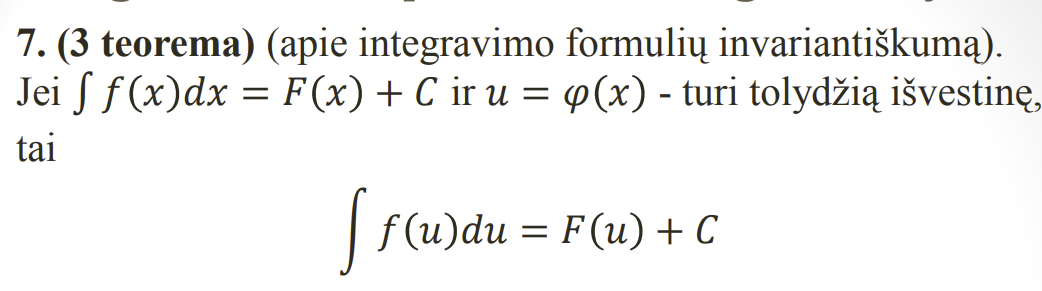
Pagrindines neapibreztinio integralo savybes

.

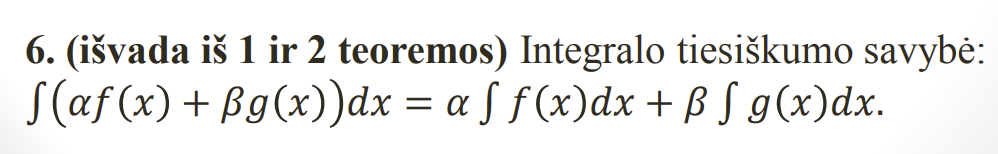
Integravimas dalimis

.

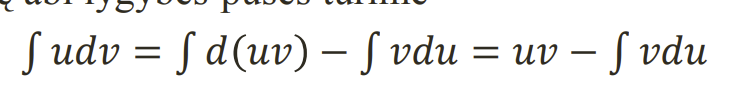
Kreivines trapecijos plotas

Atkarpa padalinkime i n daliu

Kiekvienoje dalyje pasirinkime po taska c ir suraskime funkcijos reiksme

Kiekviena atkarpa galime laikyti staciakampio pagrindu Δxi = xi - xi-1

Gauname laiptuota figura

Kiekvieno staciakampio plotas bus f(ci)Δxi

Apibreztinis integralas

Jei egzistuoja baigtine integralines sumos riba, nepriklausanti nuo atkarpos padalijamo budo bei parinktu ci tasku, tai si riba vadinama funkcijos

Skaiciai a ir b vadinami apatiniu ir virsutiniu integravimo reziais

Apibreztinio integralo savybes

.

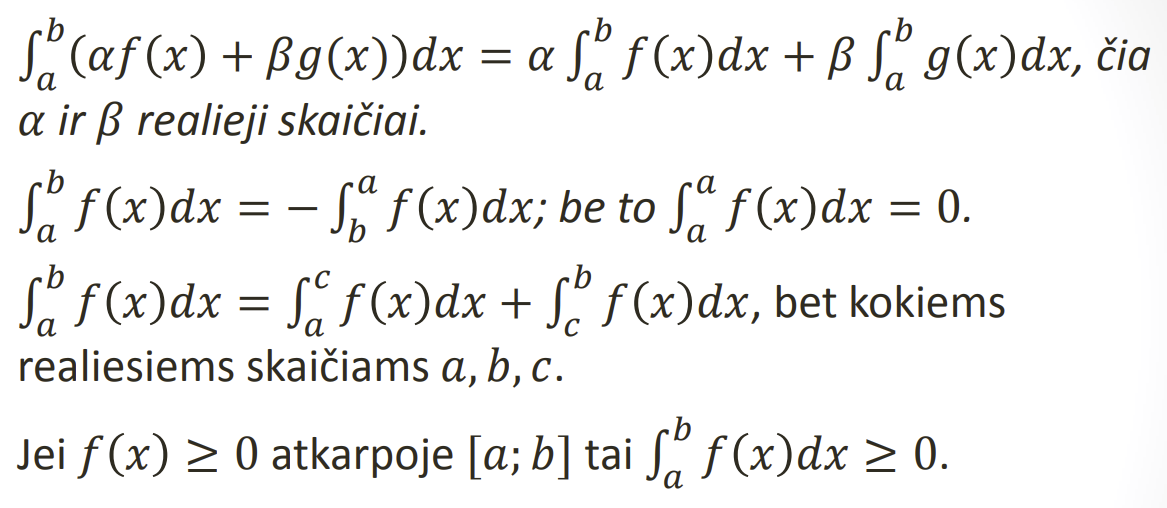
Apibreztinio integralo savybes

.

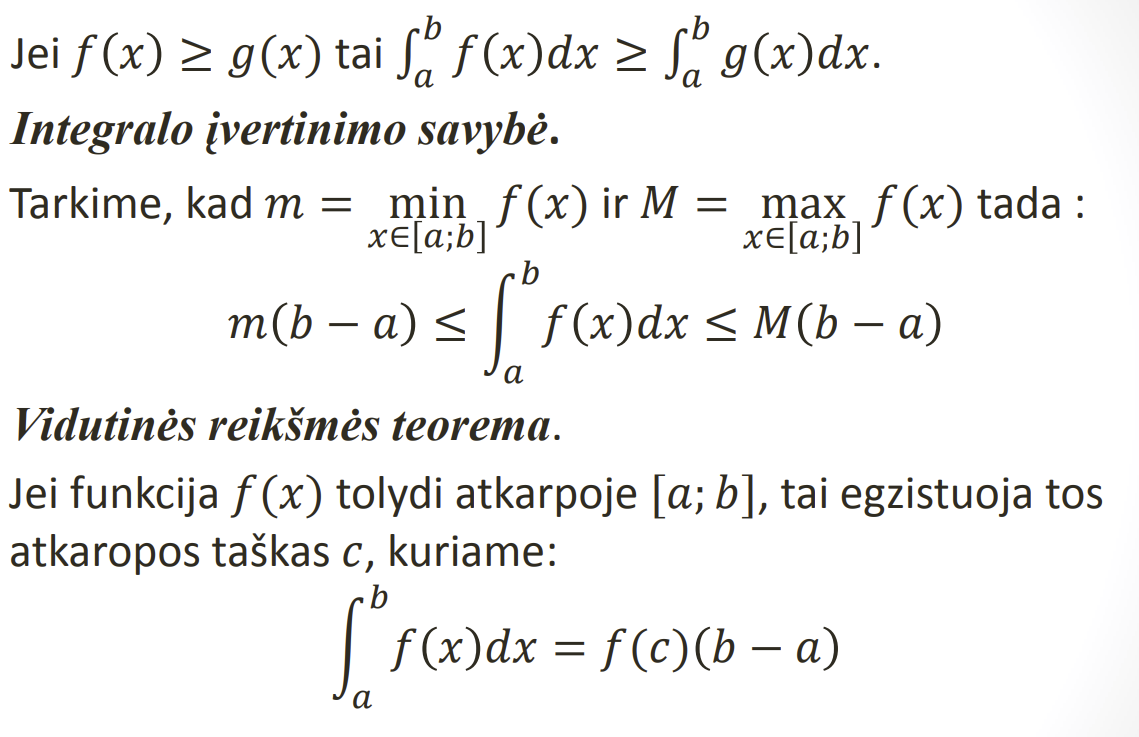
Niutono ir Leibnico formule

Jei funkcija f(x) tolydi atkarpoj [a;b] ir F(x) tai

Apibreztinio integralo integravimas dalimis

.

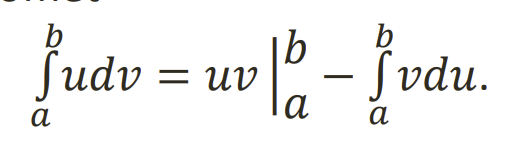
Netiesioginis integralas

Jei baigtine integralo riba, kai b → +inf tai ji vadinama

Ir zymima

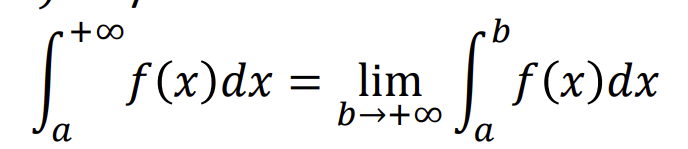
Konverguoja

Jei riba baigtine tai sakome kad integralas

Diverguoja

Kai riba begaline arba neegzistuoja

Netiesioginiu integralu su begaliniais reziais nustatymas naudojant palyginima

Jei su visomis reiksmemis teisinga nelygybe 0 <= f(x) <= g(x)

tai jei integralas +∞→a g(x) koverguoja tai konverguoja ir f(x)

jei integralas +∞ → a f(x) diverguoja tai diverguoja ir g(x)

Absoliutus ir reliatyvus netiesioginiu integralu konvergavimas

.

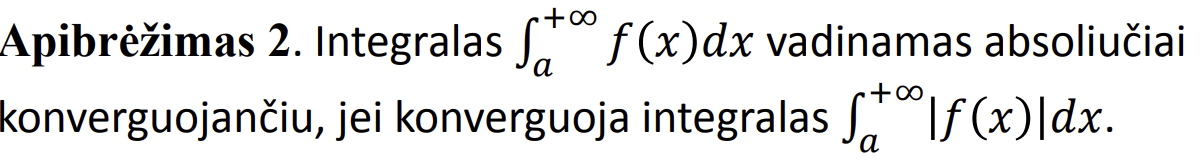
Absoliutus ir reliatyvus netiesioginiu integralu konvergavimas teorema

.

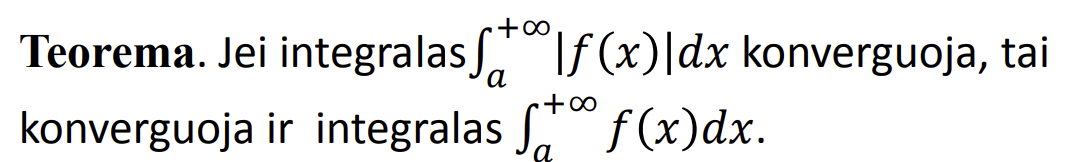
Absoliutus ir reliatyvus netiesioginiu integralu konvergavimas

.

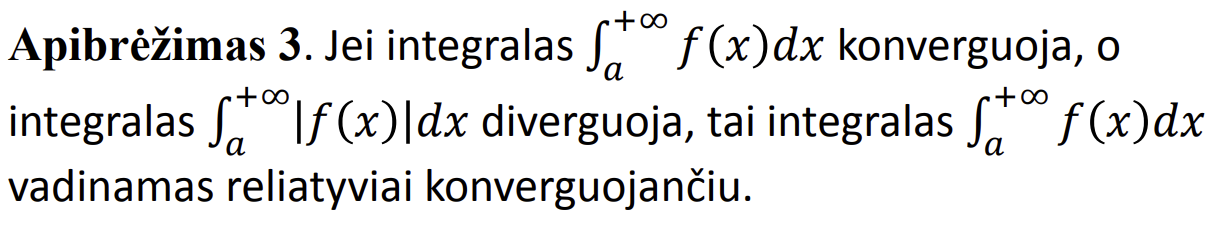
Jei figura riboja dvieju funkciju f(x) ir g(x) grafikai

.

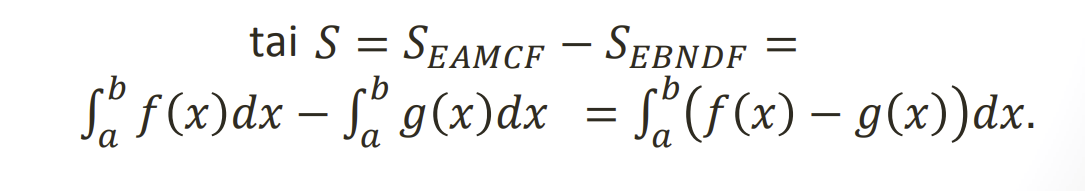
Kreives lanko ilgis L

vadinama riba prie kurios arteja ibreztos i ta kreive lauzties ilgis

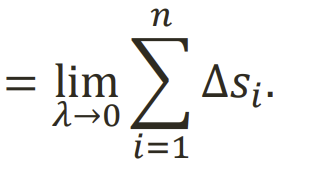
Alternuojanti skaiciu eilute

Eilute kurios gretimi nariai skiraisi zenklu

Daline suma

.

Konverguoja

Jei egzistuoja eilutes daliniu sumu sekos baigtine riba lim n → ∞ Sn = S tai sakome kad eilute

Diverguoja

Kai lim n → inf Sn yra begaline/neegzistuoja tai sakoma kad eilute -

Tokia eilute sumos neturi

Konverguojančių eilučių savybės

Is konverguojancios eilutes ateme arba prideje baigtini skaiciu nariu, gauname konverguojancia eilute

Jei eilute a1+a2+a3+an konverguoja ir suma lygi S tai eilute ca1 + ca2+ ca3+ can taip pat konverguoja

Jei eilutes a1+a2+a3+an ir b1+b2+b3+bn konverguoja o sumos lygios S ir Z tai eilute (a1+b1)+(a2+b2)

Palyginimo pozymis

Konverguos/Diverguos ir A ir B eilutes

Jei eiluciu A ir B nariai teigiami

Ribinis palyginimo pozymis

Jeigu eiluciu A ir B nariai teigiami ir egzistuoja baigtine nelygi nuliui riba, tai nagrinejamos eilutes arba konverguoja arba diverguoja

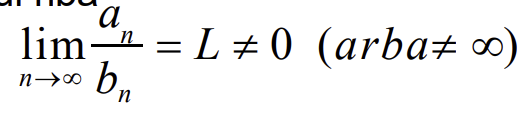
D’Alambero pozymis

Jeigu eilutes nariai teigiami ir egzistuoja riba, tai

eilute konverguoja kai L < 1

eilute diverguoja kai L > 1

Jei L = 1 tai negerai parinktas pozymis

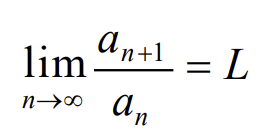
Kosi radikalusis pozymis

Jeigu eilutes nariai teigiami ir egzistuoja riba tai

eilute konverguoja kai L < 1

eilute diverguoja kai L > 1

jei L = 1, negerai parinktas pozymis

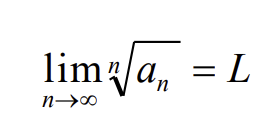
Kosi integralinis pozymis

f(x) tolydi, teigiama ir monotoniskai mazejanti funkcija [k; +∞)

Jei skaiciu eilutes nariai teigiami ir isreiskiami formuke an = f(n) n=k>=1, eilute konverguoja/diverguoja kai konverguoja/diverguoja integralas +∞ → k f(x)dx

Absoliuciai konverguojanti eilute

Kintamo zenklo eilute vadinama ___ jei konverguoja is jos moduliu sudaryta eilute

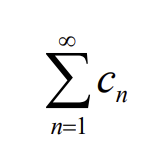
Reliatyviai konverguojanti eilute

Kai kintamo zenklo eilute konverguoja, o moduliu eilute diverguoja, tai sakoma

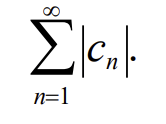
Funkcine eilute

Eilute kurioje visi demenys yra funkcijos vadinama

Funkciju eilutes konvergavimo sritis

Aibe tu x reiksmiu su kuriomis eilute konverguoja

Laipsnine eilute

Funkciju eilute kur x yra kintamasis o c realieji skaiciai

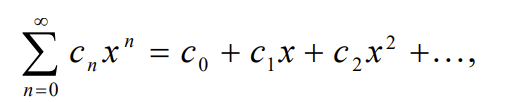
Laipsnines eilutes konvergavimo intervalo nustatymas

Remiames D’Alambero arba Kosi radikaliniu pozymiu. Skaiciuojame ribas, reikalaujam kad L(x) < 1

Teiloro eilute

Taikoma kai nagrinejama funkcija nera apibrezta taske x=0 arba isvestines neapibreztos

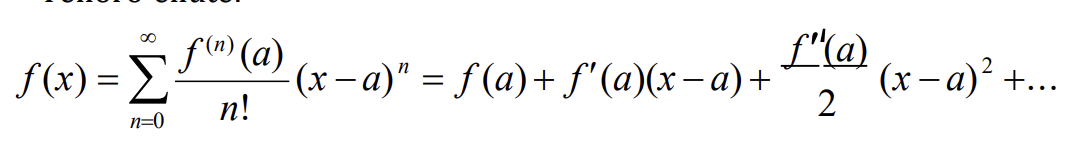
Makloreno eilute