Ordinary Differential Equations (Introduction)

What is an ODE?

An equation involving derivatives of a function of one variable

Order

Highest derivative in the equation

Solution

Function that satisfies the equation

Classifying ODEs

Order

Linearity

Homogeneity

Autonomy

General form of a first order ODE

dy/dt = f(t,y)

What form indicates the 1st order ODE is separable?

dy/dt = g(t) * h(y)

Form of a linear ODE

dy/dx + P(x)y = Q(x)

How do we solve a first order linear ODE?

Integrating factor

What is an exact ODE?

If M(x,y)dx + N(x,y)dy = 0

And dM/dy = dN/dx

Bernoulli equation

dy/dx + P(x)y = Q(x) y^n

How do we solve a Bernoulli ODE?

Substitute u = y^(1-n)

Second order ODE general form

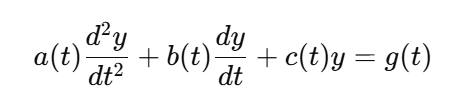
How do you tell if a second order linear ODE is homogenous?

g(t) = 0

How do you solve a homogenous second order ODE?

Find the auxiliary equation

Roots determine solution type

What is the general solution for non homogenous second order ODEs?

y = yh + yp

yh is solution to homogenous equation, yp is particular solution

Methods to find yp

Undetermined coefficients

Variation of parameters

How do we solve systems of ODEs?

Use eigenvalue method for linear systems

General form of first order ODE system

dx*/dt = Ax*

General solution to first order ODE system

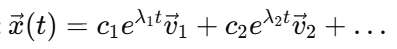
Autonomous systems

dx/dt = f(x,y)

dy/dt = g(x,y)

Equilibrium points where f(x,y) = g(x,y) = 0

How do we address autonomous systems?

Using phase plane analysis

Linearise near critical points by finding Jacobian matrix J

How do we address non linear systems?

Linearise at equilibrium using Jacobian

What does linearisation look like?

dx*/dt = Jx*

Jacobian matrix for 2D autonomous system

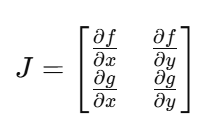
How do we evaluate at equilibrium?

f(x*, y*) = 0

g(x*, y*) = 0

Solve to find equilibrium points and evaluate J at these points