Chapter 1: Background

Vectors

These specify the magnitude and direction.

Scalars

These specify the magnitude and no direction.

Speed

indicates how fast an object is moving but not in what direction.

Velocity

indicates both how fast an object is moving and in what direction.

arrow

A vector is generally represented by an \_____ whose direction is in the direction of the vector and whose length is proportional to the vector’s magnitude.

positive

To multiply a vector by a \_________ scalar , simply multiply the vector’s magnitude by the scalar.

negative

To multiply a vector by a \________ scalar , change the vector’s magnitude and reverse the direction of the vector.

Speed

Indicates how fast an object is moving but not in what direction.

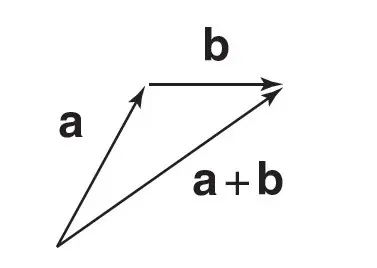
Vector Addition

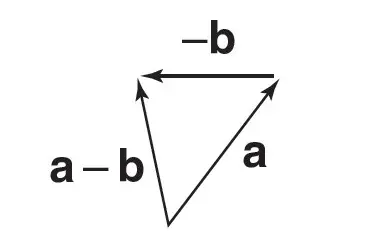
Vector Subtraction

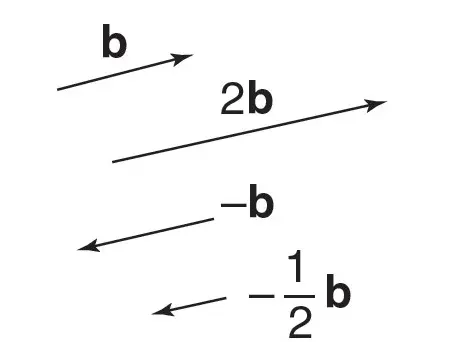
Scalar Multiplication

perpendicular

If two vectors are \________ , their dot product will equal zero [cos(π/2) \= 0].

parallel

If two vectors are \_______ , their dot product will equal the product of their magnitudes (cos 0 \= 1).

antiparallel

If two vectors are \_________ , their dot product will be the negative of the product of their magnitudes [cos(π) \= −1].

Scalar Product

Dot product is also known as?

third

The cross product of two vectors yields a \____ vector.

Vector Product

Cross product is also known as?

units

All measurements and observable quantities have \________; otherwise they would be meaningless.

Multiplication and division

Units are multiplied and divided just as variables are.

Addition and subtraction

The sum or difference of two quantities with the same units has those same units.

Exponential function

The argument x of an \__________, such as ex, must be dimensionless, such as the ratio of two lengths.

dimensionless

Arguments of trigonometric functions, such as sinx and tan−1x , also must be \___________