Chapter 3: Quadratics

Core and Extension, some sketching as well.

Distributive Laws

a(b±c) = ab±ac

(a+b)(c+d) = ac+ad+bc+bd

Perfect Squares

(a+b)² = a²+2ab+b²

(a-b)² = a²-2ab+b²

Difference of Perfect Squares (DOPS)

(a+b)(a-b) = a²-b²

Factorisation

1. Taking out the common factors

2. Grouping terms (X = ac, + = b)

   e.g. x²+3x-10 → 5*-2 = -10 = ac, 5+(-2) = c = b

   = x²+5x-2x-10

   = x(x+5)-2(x+5)

   = (x-2)(x+5)

Monic Quadratics

x²+(m+n)x+mn = (x+m)(x+n)

Non - Monic Quadratic Trinomials

1. Two numbers to give a*c and b when a+c;

2. Split bx, then factorise by grouping.

e.g. 6x²+19x+60

15×4 = 60

∴ 6x²+4x+15x+60

=3x(2x+5) + 2(2x+5)

= (3x+2)(2x+5)

Tip: How to find perfect squares (completely optional ;)

1. Check if a/c are square numbers

2. check if a*c/2 = b

3. If all are satisfied, then it is a perfect square (depending on the positivity of bx; if positive, the square is positive, or vice versa).

e.g. 16x²-40x+25

16x² = (4x)²

25 = (5)²

16×5/2 = 40 (ignore pos/neg here)

∴(4x-5)².

Completing the Square

BHS Rule: add and substract (b/2)² - factorise by DOPS (surd allowed).

Quadratics Formula and the Discriminant

Quadratics Formula: (-b±√(b²-4ac))/(2a).

Discriminant (denoted by the greek letter delta ‘Δ’): b²-4ac

When Δ < 0, no real solutions (as √Δ = √-num, undefined)

When Δ = 0, real solution (x = -b/2a)

When Δ > 0, 2 real solutions (x = quadratics formula)

Turning Point

Formula: a(x±h)²+k=0, (±h, k) as turning point.

Second Formula: h = -b/2a, k = c-b²/4a (or sub x value to original equation)

Axis of symmetry: x = h/-h

Tip: y-int = c

Sketching by completing the square

To sketch a quadratic in y=a(x-h)²+k (from ax²+bx+c):

Determine the tp (h,k): if a is positive, tp is min; if a is negative, tp is max.

Determine y-int by x=0; (if any) determine x-int by y=0, DOPS.

Tip: to solve x²=a, a>0, take √a for roots.

Sketching using Quadratic Formula

For y=ax²+bx+c:

y-int at y=c (x=0); x-int at y=0;

Use quadratic formula for x-int:

Discriminant (Δ): b²-4ac.

If Δ < 0, no real solutions (√-num =?)

If Δ = 0, one real solution (x=-b/2a, the only x intercept is the tp)

If Δ > 0, two real solutions (quadratic formula)

Sketching using Factorisation

To sketch a graph of a monic equation y=x²+bx+c:

Find y-int by sub x=0; find x-int by sub y=0 and factorise using the Null Factor Law.

Note: Null Factor Law: if a*b=0 then a=0/b=0

The tp is the axis of symmetry; use two x-values/int, sum, and divide by two.

Sub this x-value to find y coordinate of tp.

Sketching using Transformations

y=a(x-h)²+k

tp = (h,k), axis of symmetry at x = h

If a>0, the parabola is upright; a<0, inverted.

Solving Quadratic Inequalities

Inequality Symbols

• "<" or ">": Use an opened circle + arrow indicating directions when graphing / Shading.
  Example: x² - 4 > 0 → dashed curve at x = -2 and x = 2, shading outside.

• "≤" or "≥": Use a closed circle + arrow indicating directions when graphing / Shading.
  Example: x² - 4 ≤ 0 → solid curve at x = -2 and x = 2, shading between the roots.

---

Shading Direction

• "<" or "≤": Solution is inside the curve.
  Answer: value < x < value.
  Example: x² - 4 ≤ 0 → answer: -2 ≤ x ≤ 2 (shade between the roots).

• ">" or "≥": Solution is outside the curve.
  Answer: x < value or x > value.
  Example: x² - 4 > 0 → answer: x < -2 or x > 2 (shade outside the roots).

• NOTE: WHEN NEGATIVE, REVERSE EVERYTHING.

Discriminant: Advanced

• If Δ = b²-4ac is a perfect square i.e., 1,4,9, etc. and Δ≠0, two rational solutions.

• If Δ = b²-4ac = 0, one rational solution

• If Δ = b²-4ac is NOT a perfect square and Δ>0, two irrational solutions.

Solving Simultaneous Linear and Quadratic Equations

1. Form the quadratic equation.

• ax² + bx + c1 = mx + c2

2. Rearrange the equation so that the right-hand side is zero:

• ax² + (b − m)x + (c1 − c2) = 0

3. Solve equation for x and substitute x-values into LINEAR EQUATION to find the y-values.

• If ∆ > 0, two intersection points.

• If ∆ = 0, one intersection point.

• If ∆ < 0, no intersection points.

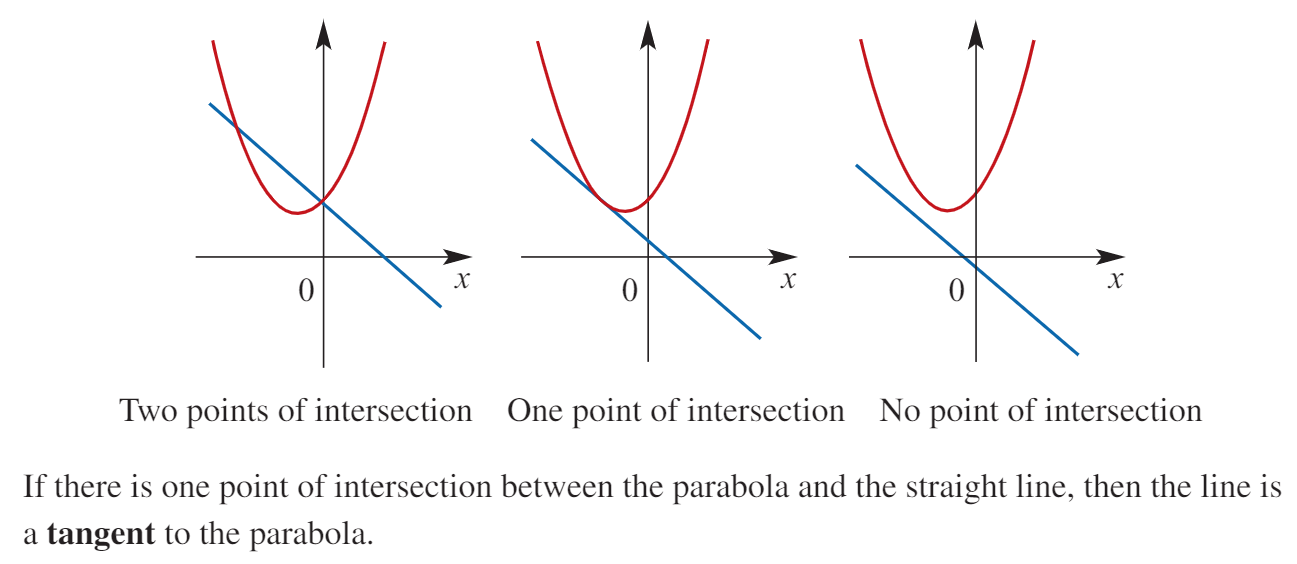
Families of Quadratic Equations

1. y = a(x − e)(x − f) - This can be used if two x-axis intercepts and the coordinates of one other point are known.

2. y = a(x − h)² + k - This can be used if the coordinates of the turning point and one other point are known.

3. y = ax² + bx + c - This can be used if the coordinates of three points on the parabola are known.