TRIGONOMETRY 1: Common Radian Measurements and the Unit Circle

π/6

30°

π/4

45°

π/3

60°

π/2

90°

2π/3

120°

3π/4

135°

5π/6

150°

π (in degrees)

180°

7π/6

210°

5π/4

225°

4π/3

240°

3π/2

270°

5π/3

300°

7π/4

315°

11π/6

330°

2π

360°

Radian → Degree formula

(Radian) * (180/π)

Treat π like a variable and cancel it out top and bottom of the fraction

Degree → Radian formula

(Degree) * (π/180)

Treat π like a variable and leave it as itself

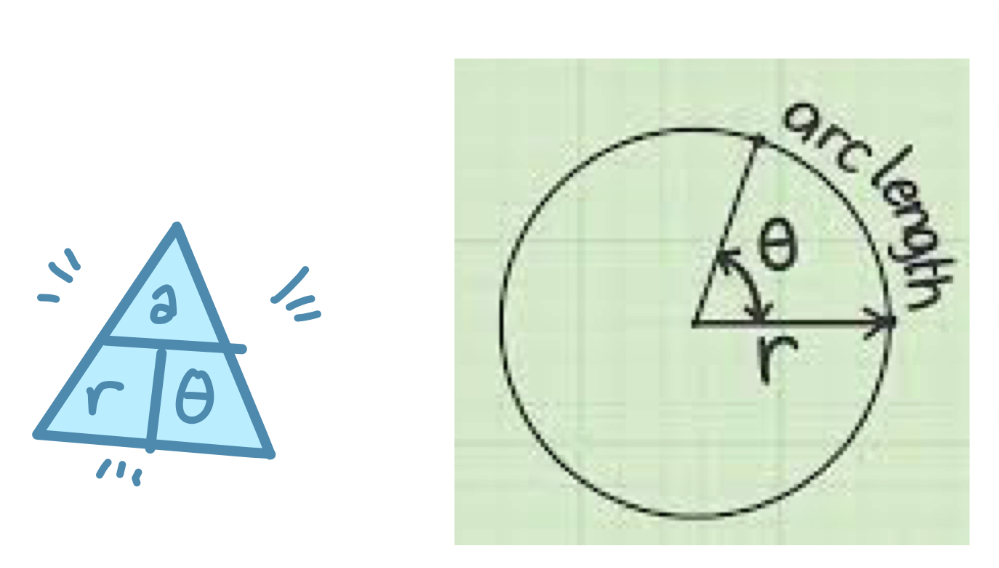
Arc Length Formula

a/r = θ

a = arc length (any distance measure)

r = radius (same as “a”)

θ = angle of the section (MUST be in radians)

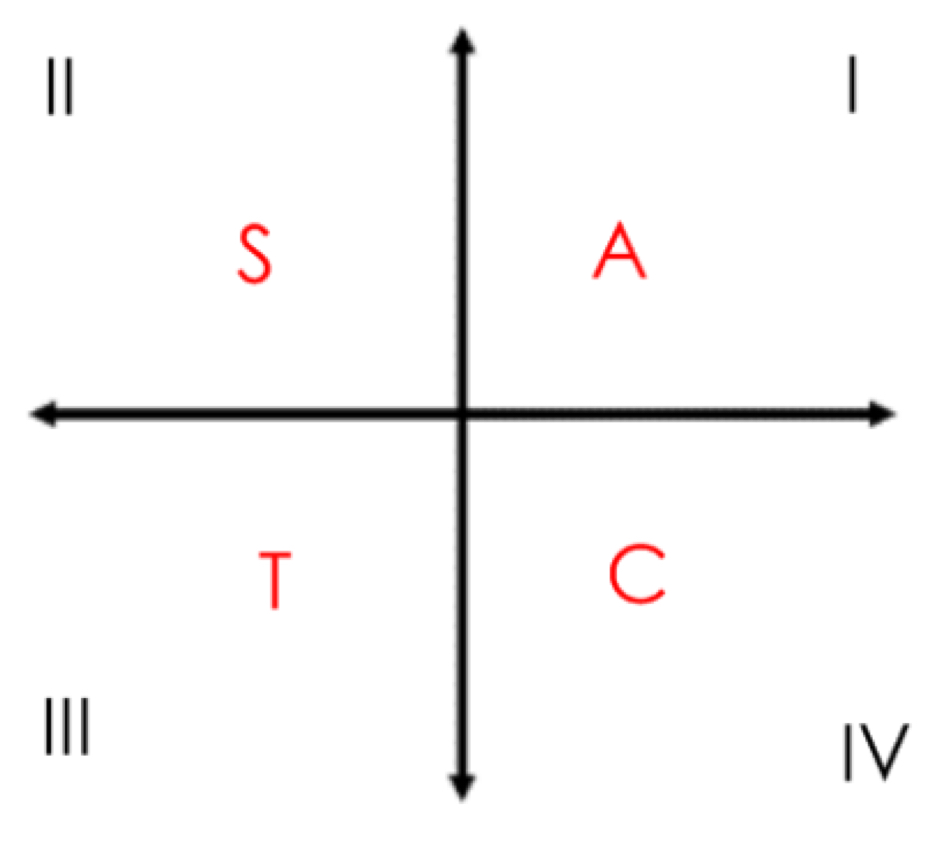
CAST rule and Quadrants

csc

Cosecant, reciprocal of sine (1/sin)

O/H → H/O

sec

Secant, reciprocal of cosine (1/cos)

A/H → H/A

cot

Cotangent, reciprocal of tangent (1/tan)

O/A → A/O

Within the Unit Circle, is sin x or y? What about cos? What about tan?

(x, y) → (cos, sin)

tan = y/x

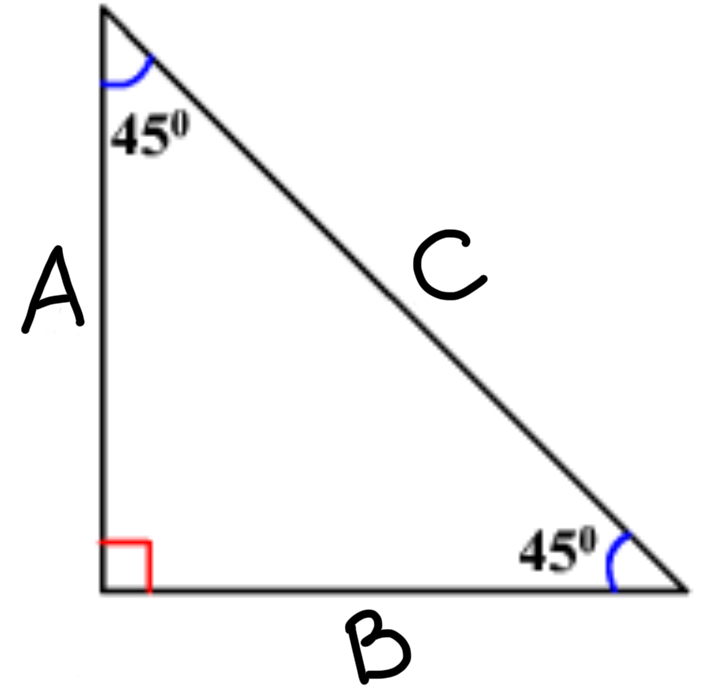
Label this special triangle (unit circle style)

A: √2 / 2

B: √2 / 2

C: 1

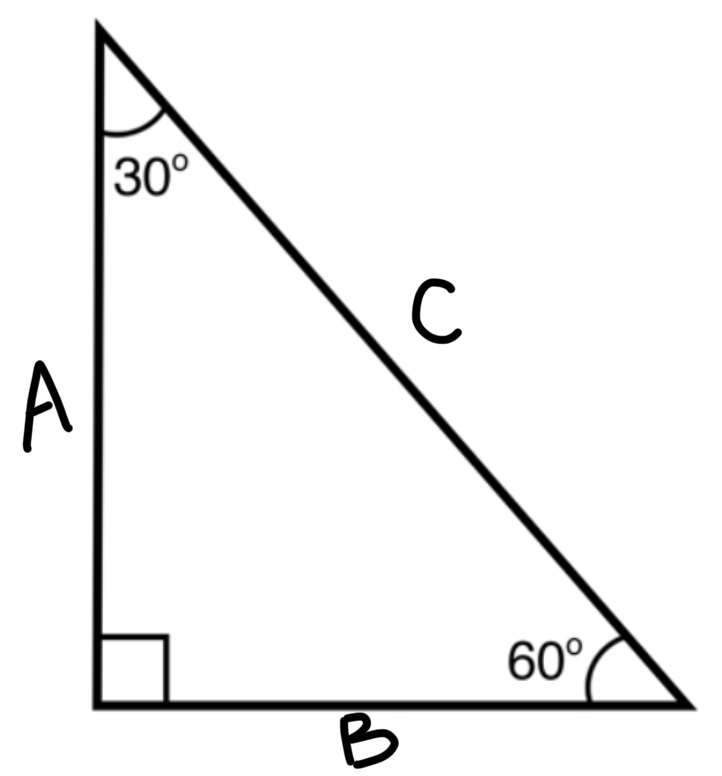
Label this special triangle (unit circle style)

A: √3 / 2

B: 1 / 2

C: 1

π/6 (unit circle coordinates)

X: √3/2

Y: 1/2

π/4 (unit circle coordinates)

X: √2 / 2

Y: √2 / 2

π/3 (unit circle coordinates)

X: 1 / 2

Y: √3 / 2

0/ 2π (unit circle coordinates)

(1,0)

π/2 (unit circle coordinates)

(0,1)

π (unit circle coordinates)

(-1,0)

3π/2 (unit circle coordinates)

(0,-1)