C9: Experiments with more than 1 independent variable

What’s a 2×2 factorial design? What are the characteristics?

Amount of numbers indicates how many independent variables (IV) there are

• 2 IV

Number indicates how many conditions/levels there are for each IV

• 2 conditions for each

• 4 conditions total

→ ex. 2×2×2 factorial design: 3 IVs & 2 levels for each IV

IV crossed with each other

IV manipulated or measured

IV at within- or between-subject level (or combination)

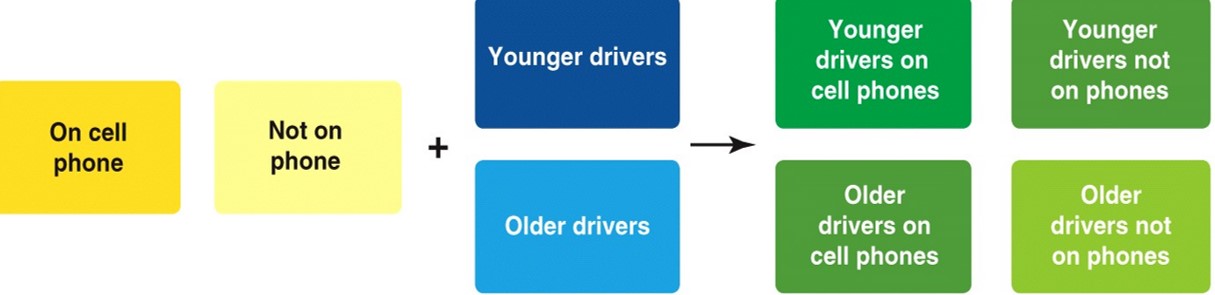
Why are factorial designs used?

To observe if there’s an interaction effect

• interaction between the 2(+) IVs?

What are the 2 main purposes of factorial designs?

1) Testing the boundaries of effects

• ex. does effect of cell phone use on breaking onset depend on age of the driver?

2) Testing theory

• ex. are drunk people more aggressive, because alcohol is implicitly associated with aggression?

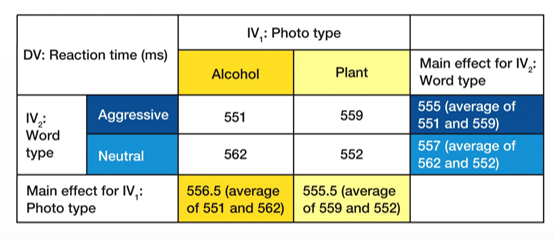
What is a main effect & how can you calculate this?

The average effect of one independent variable on the dependent variable, across the different levels of the other independent variable(s)

Calculation:

• compare marginal means

• take average of one level of an IV (ex. (551+559)/2 = 555)

• compare that to average of other level (ex. 557)

• if there’s a difference, there’s a main effect

• ex. there’s a main effect for word type

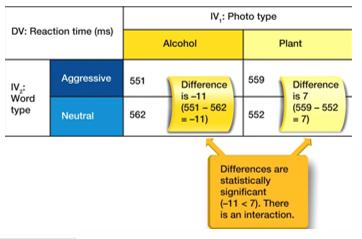
What is an interaction effect & how can you calculate this?

The effect of one independent variable on the dependent variable, conditional on the value of another independent variable

• moderator

• “a difference in differences”

Calculation:

• compare one level of an IV to the other condition of that IV

• subtract scores from each other

• if there’s a difference, there’s an interaction effect

• ex. there’s an interaction effect between word & photo type

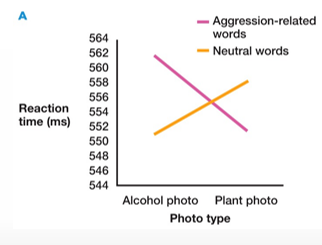
How can you check for an interaction effect using graphs?

If lines cross, are not parallel → interaction effect

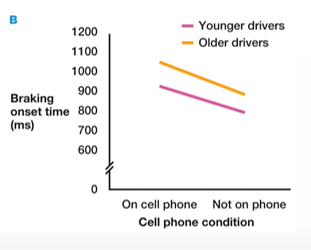
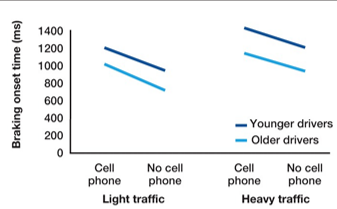
How can you check for a main effect using graphs? You can explain this using the example of the use of a cell phone (or not) while driving with young & old drivers.

Check main effect of age:

• the lines don’t overlap, older drivers have a systematically higher RT than young drivers → there is an effect of age

Check main effect of cell phone:

• compare first 2 scores with other 2 scores (cell phone vs no cell phone)

• there’s a decrease/difference → there’s an effect of cell phone use

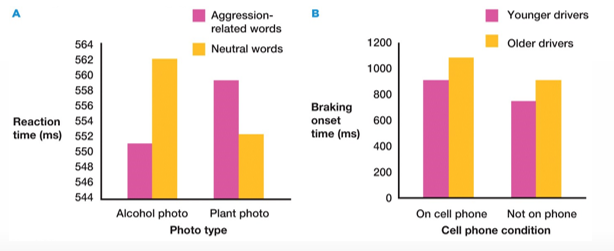
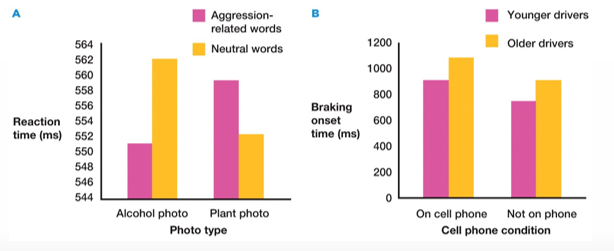
How can you check for main or interaction effects using histograms?

You can mentally draw lines from one point to another (colour to colour)

• if lines cross → interaction effect

Which kind of effect is more important in factorial designs?

Interaction effects

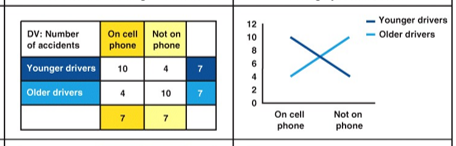
Is there a main effect? Is there an interaction effect? If yes, for which variables?

No main effect

Interaction effect age x cell phone:

• younger drivers on a phone cause more accidents, whereas older drivers on a phone cause fewer accidents

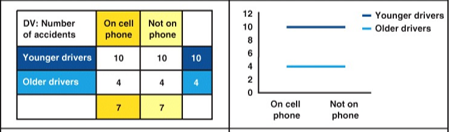
Is there a main effect? Is there an interaction effect? If yes, for which variables?

Main effect only for age

• younger drivers cause more accidents than older drivers

No interaction effect

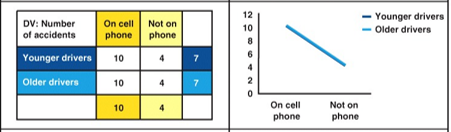
Is there a main effect? Is there an interaction effect? If yes, for which variables?

Main effect only for cell phone use

• regardless of being a younger or older driver, being on your cell phone causes more accidents

No interaction effect

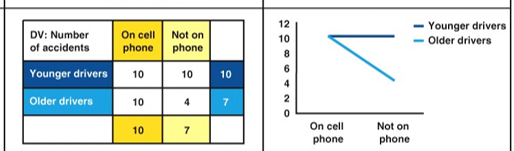
Is there a main effect? Is there an interaction effect? If yes, for which variables?

Main effect of both age & cell phone use

• younger drivers have more accidents

• cell phone causes more accidents

Interaction effect

• older drivers on the phone cause more accidents, but for younger drivers it doesn’t matter whether they’re on the phone or not

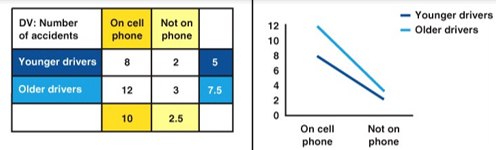
Is there a main effect? Is there an interaction effect? If yes, for which variables?

Main effect for both age & cell phone use

• older drivers have more accidents

• cell phones causes more accidents

Interaction effect

• cell phone use has a bigger impact on older drivers

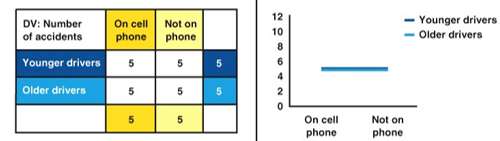
Is there a main effect? Is there an interaction effect? If yes, for which variables?

No main or interaction effect

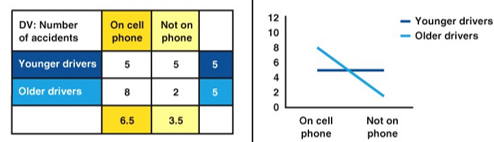
Is there a main effect? Is there an interaction effect? If yes, for which variables?

Main effect only for cell phone

• cell phone use causes more accidents

Interaction effect

• cell phone use only impacts older drivers

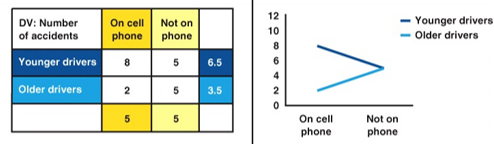
Is there a main effect? Is there an interaction effect? If yes, for which variables?

Main effect only for age

• younger drivers have more accidents

Interaction effect

• cell phone use has different effects depending on whether you’re a young or old driver

• older drivers on the phone cause fewer accidents, whereas younger drivers on the phone cause more accidents

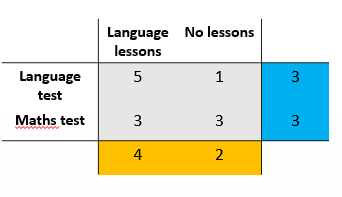
How could you explain the main effects of this table?

“There is a main effect of training type, such that the language lessons group scored higher than the group that received no lessons.”

“There is no main effect of test type.”

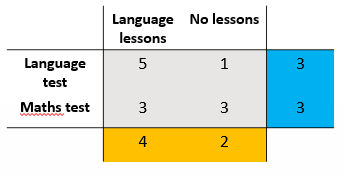
How could you explain the interaction effects of this table?

Each interaction is different

Describe simple main effects separately

• simple main effect = effect of one independent variable on dependent variable, within a single level of another independent variable

“There is an interaction effect, such that the language lessons group scored better than the no lessons group on the language test. Both groups scored similarly on the maths test.”

• rows

“Language lessons group scored higher on language than maths test.”

• columns

What are 5 variants of factorial designs?

1) Between-group factorial design

2) Within-group factorial design

3) Mixed factorial design

4) Number of levels of the independent variables

• ex. 3×4

5) Number of independent variables

• ex. 2×2×2

What are the implications for the number of participants when the IV are manipulated at within- vs between-groups level (in a factorial design)?

Between-groups level → more participants needed

Within-groups level → less participants needed

What are mixed factorial designs?

Both within- & between-groups level

• ex. groups only see neutral or aggression-related words (between subjects) but see alcohol and plant photos (within subjects)

What are the implications for ANOVA with each type of (factorial) design (within-/between-subjects/mixed)?

ANOVA assumes that data are independent, but that’s not the case for within-subject or mixed designs

→ Repeated measures for example

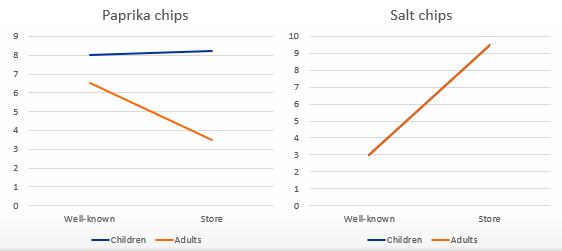
This is a 2×2×2 factorial design. What kinds of effects are seen?

A) Interaction effect (effect of brand of paprika chips only for adults) & main effect of age (children give higher ratings) & brand (well-known brands are rated higher)

B) No interaction effect, main effect only for brand (store brands rated higher)

→ Interaction between interaction effect

• effect of brand depends on age but also on the type of chips (paprika or salt)

• = 3-way interaction

See slides 23-25!

How can you check if there’s a three-way interaction using graphs?

If patterns in 2 graphs are different → three-way interaction

• = interaction between 3 IVs

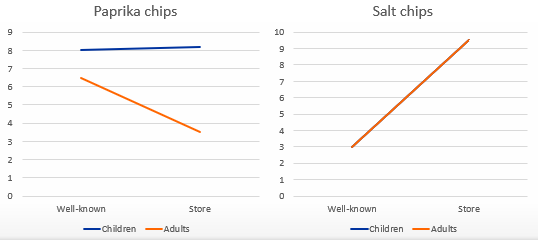
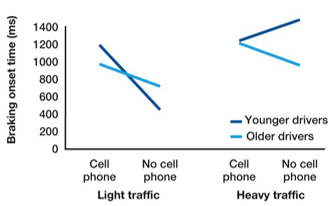
Is there a three-way interaction?

No

• no two-way interaction in left, nor right side

• 2 sides show same two-way interaction (0)

Is there a three-way interaction?

Yes

• crossing interaction on left side & spreading interaction on right side

• 2 sides show different two-way interactions

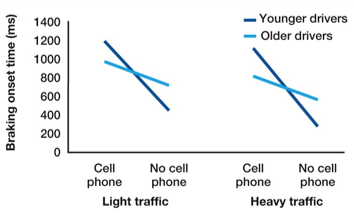
Is there a three-way interaction?

No

• two-way interaction on both sides, but interactions are the same

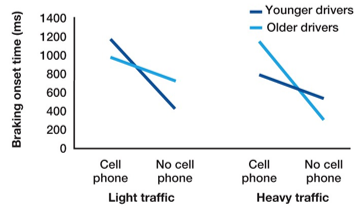
Is there a three-way interaction?

Yes

• two-way interaction on both sides

• 2 sides show different interactions (opposites here)

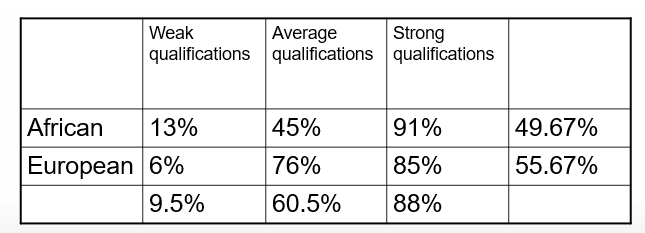
This is a 2×3 factorial design. Are there main effects? Are there interaction effects? If yes, for which variables?

Main effect of qualifications

• strong qualifications get hired way more than weak & average qualifications

Main effect for ethnicity

• Europeans get hired more often than Africans

Interaction effect

• Africans with strong qualifications get hired more than Europeans with strong qualifications

• but Europeans with average qualifications get hired way more than Africans with average qualifications

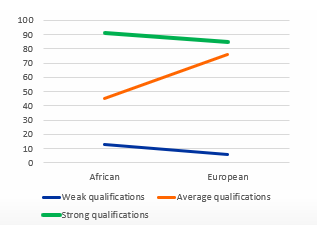
Looking at this graph, is there an interaction effect? Explain.

Yes, orange line shows different pattern than other 2

For average qualifications, Europeans have a higher chance on getting hired than Africans

• opposite for the other types of qualifications

→ Effect of being hired depends on ethnicity, but also qualification