LESSON 1-5 Engineering Data Analysis

STATISTICAL METHODS

• used to analyze data from a process to gain more sense of where in the process changes may be made to improve the quality of the process.

• designed to contribute to the process of making scientific judgments in the face of uncertainty and variation.

INFERENTIAL STATISTICS

• Involves using data from the sample to make interferences or prediction about a larger population

• similar to representational statistics (sub-sample from sample)

• make generalizations about the population from the sample

• inductive (broad to general)

• The sample along with ___ allows us to draw conclusions about the population, with ___ making clear use of elements of probability

• probability is essential in ___ because it quantifies the uncertainty in drawing conclusions about a population from a sample, enabling us to estimate the likelihood of various outcomes and make informed decisions.

DESCRIPTIVE STATISTICS

• provides general information about the fundamental statistical properties of data (e.g. mean, median, mode, variance, standard deviation, etc.)

• Measures of central tendency such as the mean, median, and mode summarize the performance level of a group of scores, and measures of variability describe the spread of scores among participants.

• can generalize from the population

• observe/describe the sample

• or deductive statistics

VARIABILITY IN SCIENTIFIC DATA

If the observed product density in the process were always the same and were always on target, there would be no need for statistical methods.

OBSERVATIONAL STUDIES

• no assigned factors, simply observe/perceive

• no parameters and variables

• qualitative research

• about experiences, norms, and culture

EXPERIMENTAL STUDIES

• with variables and parameters

• can be manipulated

MEAN, MEDIAN, MODE, RANGE

4 Descriptive Statistics

MEAN

• known as the arithmetic average, consists of the sum of all scores divided by the number of scores.

• centroid of the data; it is the point at which a fulcrum can be placed to balance a system of “weights” which are the locations of the individual data.

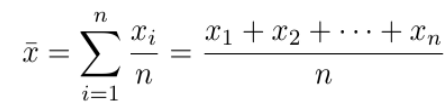
MEDIAN

• the value in the center when the numbers are arranged least to greatest

• arrange the values of the variable in order—either ascending or descending—and then count down (n + 1) / 2 score

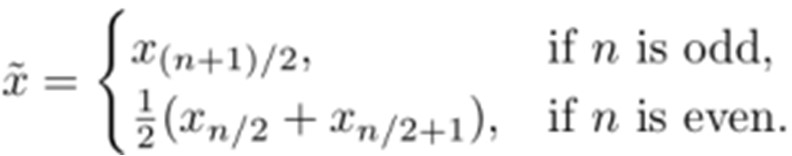
MODE

• the most commonly appearing value in a distribution

• rarely used measure of central tendency

RANGE

the difference between the largest and smallest number

DATA

• facts, figures and information collected on some characteristics of a population or sample

• can be classified as qualitative or quantitative data

UNGROUPED DATA

• data which are not organized in any specific way

• collection of data as they are gathered

• randomized raw data

STATISTIC

measure of a characteristic of sample

CONSTANT

characteristic or property of a population or sample which is common to all members of the group.

GROUPED DATA

raw data organized/arranged into groups or categories with corresponding frequencies.

PARAMETER

the descriptive measure of a characteristic of a population

VARIABLE

• measure or characteristic or property of a population or sample that may have a number of different values

• differentiates a particular member from the rest of the group.

ROLES OF PROBABILITY

Elements of probability allow us to quantify the strength or “confidence” in our conclusions. In this sense, concepts in probability form a major component that supplements statistical methods and helps us gauge the strength of the statistical inference.

CONFIDENCE INTERVAL

A probability that a parameter will fall between a set of values

DATA COLLLECTION

• first step in conducting a statistical inquiry

• refers to data gathering, a systematic method of collecting and measuring data from different sources of information to provide answers to relevant questions.

PRIMARY DATA, SECONDARY DATA

2 Methods of Data Collection

PRIMARY DATA

• first-hand data

• data with investigation

• ex. Survey/Questionnaire, Interview, Observation, Experiment

SECONDARY DATA

• data that already exists but is for other’s uses

• ex. Literature Review, Government Database, Commercial Database, Web Scraping

RETROSPECTIVE STUDY, OBSERVATIONAL STUDY, DESIGN EXPERIMENT

3 Methods of Data Collection in the Field of Engineering

RETROSPECTIVE STUDY

• use the population or sample of the historical data which had been archived over some period of time.

• to make sense of something

• examining data observed, stored, and recorded beforehand

• similar to secondary data

OBSERVATIONAL STUDY

• Process or population is observed and disturbed as little as possible, and the quantities of interests are recorded

• qualitative

• what is perceived?

• susceptible to biases

DESIGN EXPERIMENT

very important in engineering design and development and in the improvement of manufacturing processes in which statistical thinking and statistical methods play an important role in planning, conducting, and analyzing the data.

SURVEYS

• depend on the respondent’s honesty, motivation, memory, and his ability to respond. Sometimes answers may lead to vague data.

• can be done through face-to-face interviews or self-administered through the use of questionnaires.

6 STEPS IN DESIGNING A SURVEY

1. Determine objectives/purpose

2. Identify target population/respondents

3. Choose an interviewing method

4. Decide what questions to ask (must be cohesive)

5. Conduct interviews & collect data/information

6. Analyze results (graphs & conclusions)

PROBABILITY SAMPLING, NON-PROBABILITY SAMPLING

2 Types of Sampling Methods

SIMPLE RANDOM SAMPLING, SYSTEMATIC SAMPLING, STRATIFIED SAMPLING, CLUSTER SAMPLING

4 Types of Probability Sampling Method

CONVENIENCE SAMPLING, QUOTA SAMPLING, PURPOSIVE SAMPLING, SNOWBALL SAMPLING

4 Types of Non-Probability Sampling Method

SIMPLE RANDOM SAMPLING

• Every element in the population has an equal chance of being selected as part of the sample. It’s something like picking a name out of a hat.

• offers no control concerning the data

• cheap

SYSTEMATIC SAMPLING

• random selection only applies to the first item chosen. A rule then applies so that every nth item or person after that is picked.

• has a system

• clear order/organized

• can be biased

STRATIFIED SAMPLING

• involves random selection within predefined groups.

• determine what aspects of a sample are highly correlated with what’s being measured.

CLUSTER SAMPLING

• groups rather than individual units of the target population are selected at random for the sample.

• pre-existing groups, such as people in certain zip codes or students belonging to an academic year.

CONVENIENCE SAMPLING

• People or elements in a sample are selected based on their accessibility and availability.

• biased

QUOTA SAMPLING

• aims to achieve a spread across the target population by specifying who should be recruited for a survey according to certain groups or criteria.

• ex. only males above 40 years old

PURPOSIVE SAMPLING

Participants for the sample are chosen consciously by researchers based on their knowledge and understanding of the research question at hand or their goals.

SNOWBALL SAMPLING

• or referral sampling

• People recruited to be part of a sample are asked to invite those they know to take part, who are then asked to invite their friends and family and so on.

• similar to Pyramid Scheme

WHAT TYPE OF SAMPLING TO USE?

• Define your research goals

• Assess the nature of your population

• Consider your constraints (scopes & limitations)

• Determine the reach of your findings

• Get feedback

PURPOSE OF STATISTICAL ANALYSIS

When we conduct a study and measure the dependent variable, we are left with sets of numbers. Those numbers inevitably are not the same. That is, there is variability in the numbers.

DESCRIPTIVE STATISTICAL ANALYSIS, INFERENTIAL STATISTICAL ANALYSIS, PREDICTIVE STATISTICAL ANALYSIS, PRESCRIPTIVE STATISTICAL ANALYSIS, CAUSAL STATISTICAL ANALYSIS, EXPLORATORY DATA ANALYSIS, MECHANICAL ANALYSIS

7 Types of Statistical Analysis

MEAN, MEDIAN, MODE

3 Measures of Central Tendency

STANDARD DEVIATION, VARIANCE

2 Measure of Variability

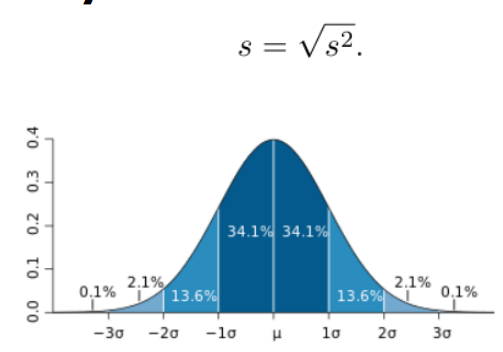
STANDARD DEVIATION

measure of the dispersion of data points in a dataset, indicating how much the values typically differ from the mean

VARIANCE

average of the squared differences between each data point and the mean, indicating the spread of data in a dataset.

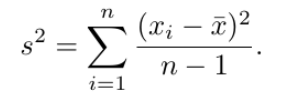
DESIGN OF EXPERIMENT

• or DOE is a tool to develop an experimentation strategy that maximizes learning using minimum resources

PLANNING, SCREENING, OPTIMIZATION, ROBUSTNESS TESTING, VERIFICATION

5 Steps in Design of Experiment

PLANNING

Identification of the objectives of conducting the experiment or investigation, assessment of time and available resources to achieve the objectives.

SCREENING

to identify the important factors that affect the process under investigation out of the large pool of potential factors.

OPTIMIZATION

to either increase yield or decrease variability or to find settings that achieve both at the same time depending on the product or process under investigation

ROBUSTNESS TESTING

to identify sources of variation and take measures to ensure that the product or process is made robust or insensitive to these factors.

VERIFICATION

• final stage involves validation of the optimum settings by conducting a few follow-up experimental runs.

• to confirm that the process functions as expected and all objectives are achieved

PROBABILITY

How likely an event is to happen

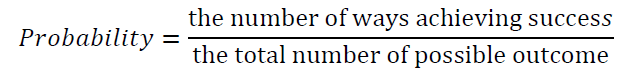
EXPERIMENT

Generates a set of data

EVENT

• Set of possible outcomes

• has 2 types: Simple and Compound

• subset of sample space

• repre

SIMPLE EVENT

one outcome

COMPOUND EVENT

more than one outcome

SAMPLE SPACE

• set of all possible outcomes or results of a random experiment

• represented by letter “S”

ELEMENT OF THAT SET

each outcome in the sample space

INTERSECTION OF EVENTS, MUTUALLY EXCLUSIVE EVENTS, UNION OF EVENTS, COMPLEMENT OF AN EVENT, PROBABILITY OF AN EVENT

5 Types of Operations of Events

INTERSECTION OF EVENTS

• intersection of two events A and B denoted by the symbol 𝐴 ∩ 𝐵

• containing all elements that are common to A and B

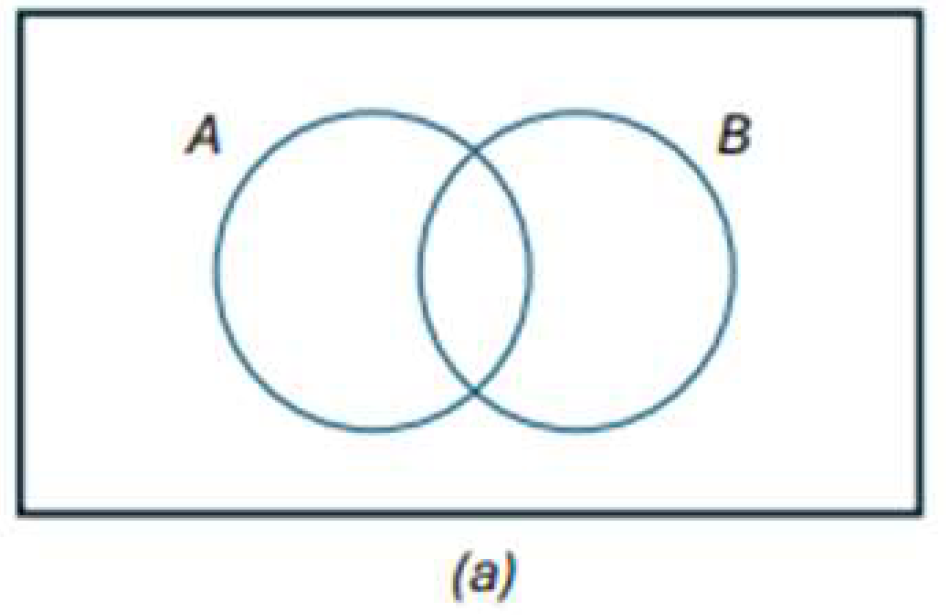
MUTUALLY EXCLUSIVE EVENTS

no elements in common

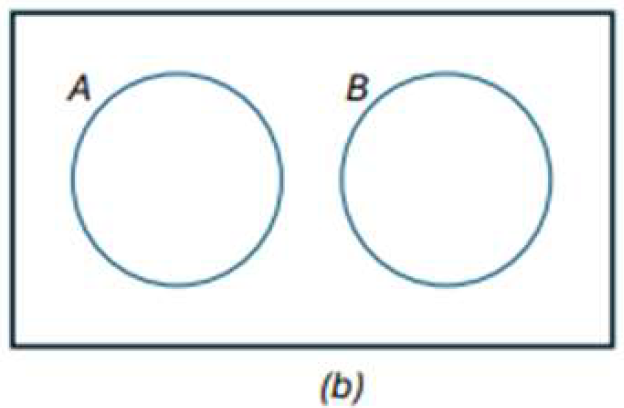
UNION OF EVENTS

• event containing all the elements that belong to A or to B or to both

• denoted by the symbol 𝐴 ∪ 𝐵

• 𝐴 ∪ 𝐵 = {𝑥|𝑥 ∈ 𝐴 𝑜𝑟 𝑥 ∈ 𝐵}

COMPLEMENT OF AN EVENT

• complement of an event A with respect to S

• all elements of S that are not in A

• denoted by A’

• the event not occurring.

• P(A')

PROBABILITY OF AN EVENT

• Sample space and events play important roles in probability

• Each probability: 𝟎 ≤ 𝑷(𝑬) ≤ 𝟏

• Sum of all probabilities: 𝑷 (𝑺) = 𝟏

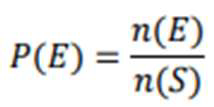
MULTIPLICATIVE RULE, PERMUTATION RULE, PERMUTATIONS WITH THINGS THAT ARE ALIKE, COMBINATIONS RULE

4 Types of Counting Rules

MULTIPLICATIVE RULE

• probability of occurrence of both the events A and B is equal to the product of the probability of B occurring and the conditional probability that event A occurring given that event B occurs

• Dependent Events: P(A ∩ B) = P(B) ∙ P(A|B)

• Independent Events: P(A ∩ B) = P(B) ∙ P(A)

PERMUTATION RULE

arrangement of all or part of a set of objects, with regard to the order of the arrangement.

PERMUTATION RULE (WITHOUT REPETITION)

PERMUTATION RULE (WITH REPETITION)

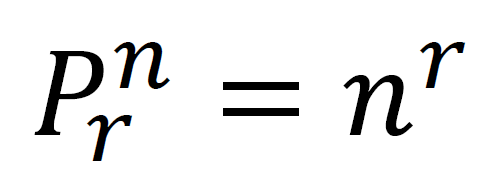
PERMUTATIONS WITH THINGS THAT ARE ALIKE

• number of permutations of n objects taken altogether, where r1 are of one kind, and r2 are of the other kind and so on

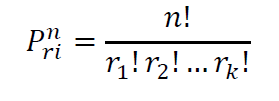
COMBINATIONS RULE

• number of ways of selecting items from a collection, such that the order of selection does not matter

• selection of objects or things out of a larger group where order doesn’t matter

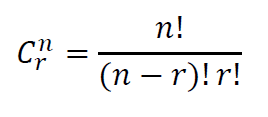
RULES OF PROBABILITY

Two events are mutually exclusive or disjoint occur at the same time.

CONDITIONAL PROBABILITY

• probability that Event A occurs, given that Event B

• P(A|B)

INTERSECTION OF A AND B

• Events A and B both occur

• P(A∩B)

• Events A and B are mutually exclusive, P(A∩B) = 0

UNION OF A AND B

• Events A or B occur

• P(A∪B)

DEPENDENT

occurrence of Event A changes the probability of Event B

INDEPENDENT

occurrence of Event A does not change the probability of Event B

RULE OF ADDITION, RULE OF MULTIPLICATION, RULE OF SUBTRACTION

3 Types of Rules of Probability

RULE OF ADDITION

• Rule 1: If two events A and B are mutually exclusive, then:

  • 𝑃 (𝐴 ∪ 𝐵) = 𝑃 (𝐴) + 𝑃 (𝐵)

• Rule 2: If events A and B are not mutually exclusive events, then:

  • 𝑃 (𝐴 ∪ 𝐵) = 𝑃 (𝐴) + 𝑃 (𝐵) − 𝑃 (𝐴 ∩ 𝐵)

RULE OF MULTIPLICATION

• Rule 1: When two events A and B are independent, then:

  • 𝑃 (𝐴 ∩ 𝐵) = 𝑃 (𝐴) 𝑃 (𝐵)

• Rule 2: When two events are dependent, the probability of both occurring is:

  • 𝑃 (𝐴 ∩ 𝐵) = 𝑃 (𝐴) 𝑃 (𝐵|𝐴)

  where,

  • 𝑃(𝐵|𝐴) = P(A ∩ B)/P(A), P(A) ≠ 0

RULE OF SUBTRACTION

• probability that event A will occur is equal to 1 minus the probability that event A will not occur

  • 𝑃 (𝐴) = 1 − 𝑃 (𝐴′)

DISCRETE DISTRIBUTION

probability of occurrence of each value of a discrete random variable

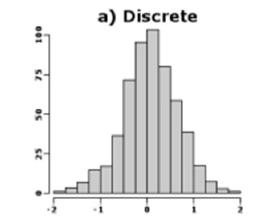
RANDOM VARIABLE

value is subject to variations due to chance (i.e. randomness, in a mathematical sense)

DISCRETE RANDOM VARIABLE

• a number that can only be one of a specific list of whole numbers

• a probability mass function which directly maps each value of the random variable to a probability.

• x has a countable number of possible values.

Examples:

1. The number of eggs that a hen lays in a given day

2. The number of people going to a given soccer match

3. The number of students that come to class on a given day

PROBABILITY HISTOGRAM

displays the probabilities of each of the three discrete random variables.

DISCRETE PROBABILITY DISTRIBUTION

Formula, Table, Graph

TABLE

Shows the values of the discrete random variable can take on and their corresponding probabilities

EXPECTED VALUE

random variable is the weighted average of all possible values that this random variable can take on.

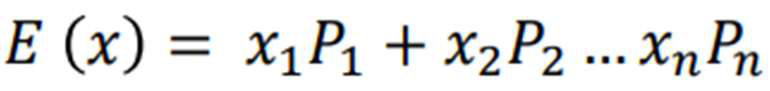
BINOMIAL RANDOM VARIABLE

number of successes x in n repeated trials of a binomial experiment

BINOMIAL DISTRIBUTION

• probability distribution of a binomial random variable

1. The experiment consists of n repeated trials.

2. Each trial can result in just two possible outcomes.

3. The probability of success, denoted by P, is the same on every trial.

4. The trials are independent

BINOMIAL PROBABILITY

probability that a binomial experiment results in exactly x successes

NOTATIONS:

• x: Number of Successes as a result of the binomial experiment

• n: Number or trials

• P: The probability of success on an individual trial

• Q: The probability of failure

• n!: The factorial n

• b(x;n,P): Binomial probability

• nCr: The number of combinations of n things taking r at a time

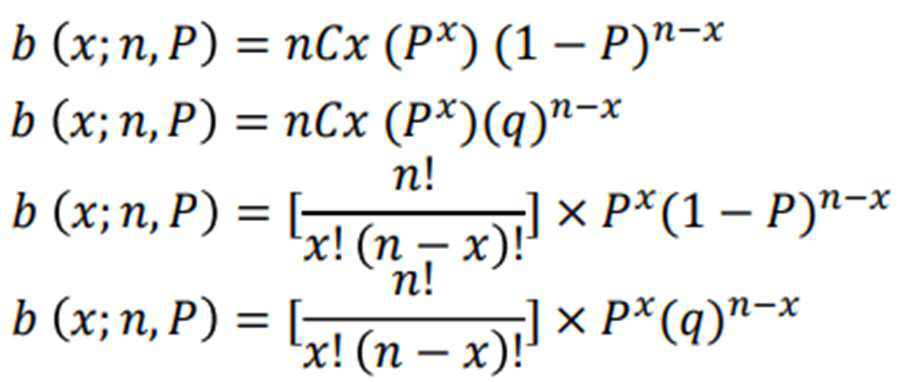
CUMULATIVE BINOMIAL PROBABILITY

probability that the binomial random variable falls within a specified range

POISSON DISTRIBUTION

probability distribution of a Poisson random variable

ATTRIBUTES

• The experiment results in outcomes that can be classified as successes or failures.

• The average number of successes (μ) that occurs in a specified region is known.

• The probability that a success will occur is proportional to the size of the region.

• The probability that a success will occur in an extremely small region is virtually zero.

NOTATIONS:

• e: constant (base of natural log), equals to 2.71828

• μ: mean number of successes

• x: actual number of successes

• P(x; μ): The Poisson Probability that exactly x successes occur in a Poisson experiment, when the mean number of successes is μ

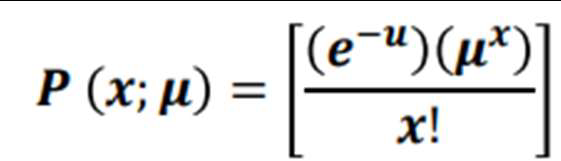
POISSON RANDOM VARIABLE

number of successes that result from a Poisson experiment.

CUMULATIVE POISSON PROBABILITY

probability that the Poisson random variable is greater than some specified lower limit and less than some specified upper limit

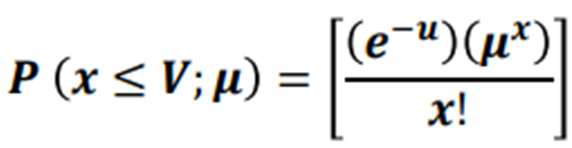
CONTINUOUS RANDOM VARIABLE

• a random variable can take on values on a continuous scale

• precisely the same values that are contained in the continuous sample space

• represent measured data, such as all possible heights, weights, temperatures, distance, or life periods