Module 4 - Signal Detection Theory

Signal detection theory

• Accounting for decision-making under uncertainty (e.g., sensory transduction noise)

• Experimental scenarios typically involve detection of a stimulus that is present in some trials but not in others.

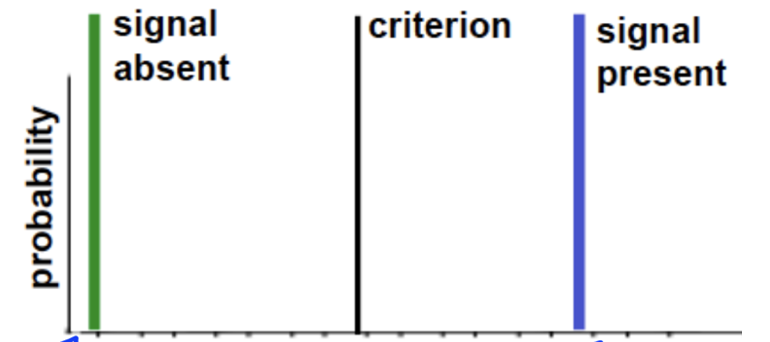
2 distributions and threshold

left one is noise, right one is signal, beta is threshold

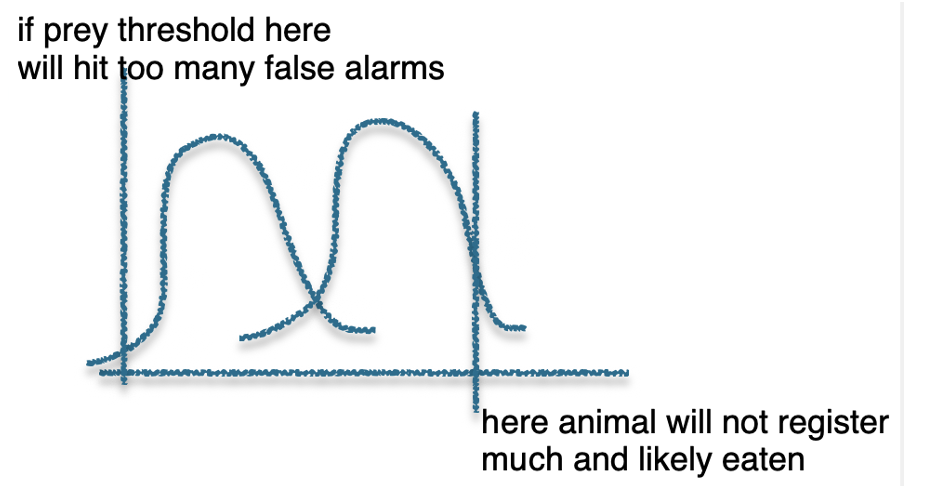
when high threshold is advantageous

imagine u are starving prey and find food, but as u approach food detect predator in distance, cannot run now, u need to eat and risk predator

so high threshold here is beneficial

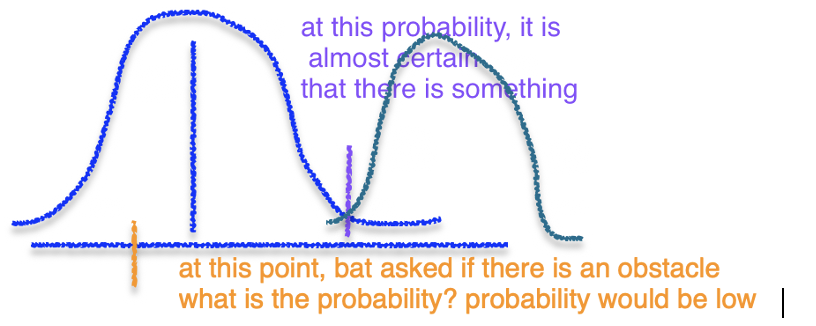
Probability density function (PDF)

are different shapes one thing common to all these distributions is that they all have an area of 1, area under the curve is 1

- probability of something happening cannot be bigger than 1

- probability of something not happening cannot be smaller than 0

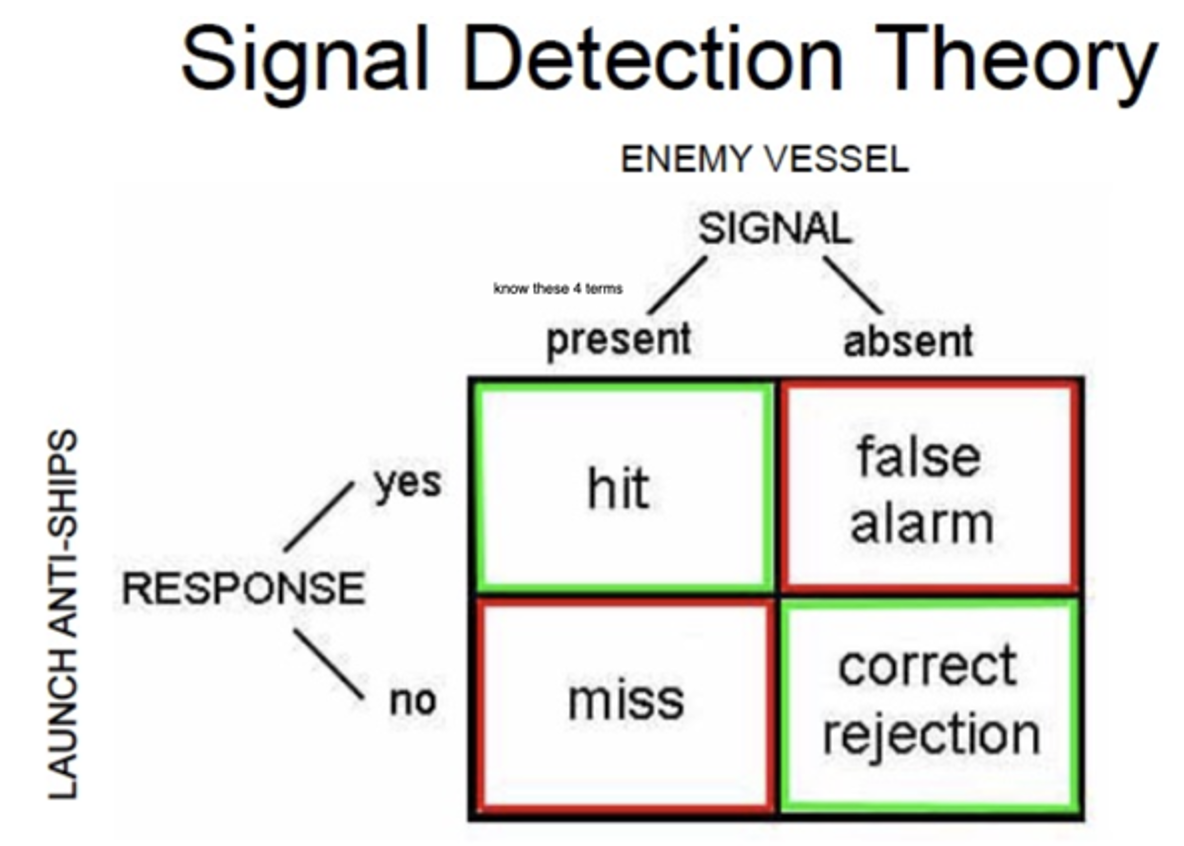
SDT four possibilities

hit, false alarm, miss, correct rejection

• Two values from each column is necessary and sufficient to reconstruct the matrix

- want sweet spot so not wastefully reactive to every stimulus

- false alarm -> waste of resource

- miss -> suffer

Ideal Observer

some species that perfectly detects every signal and responds appropriately, this does not happen in nature, should be sensitive and specific

• this ideal observes would have no overlap so long as threshold is between the means

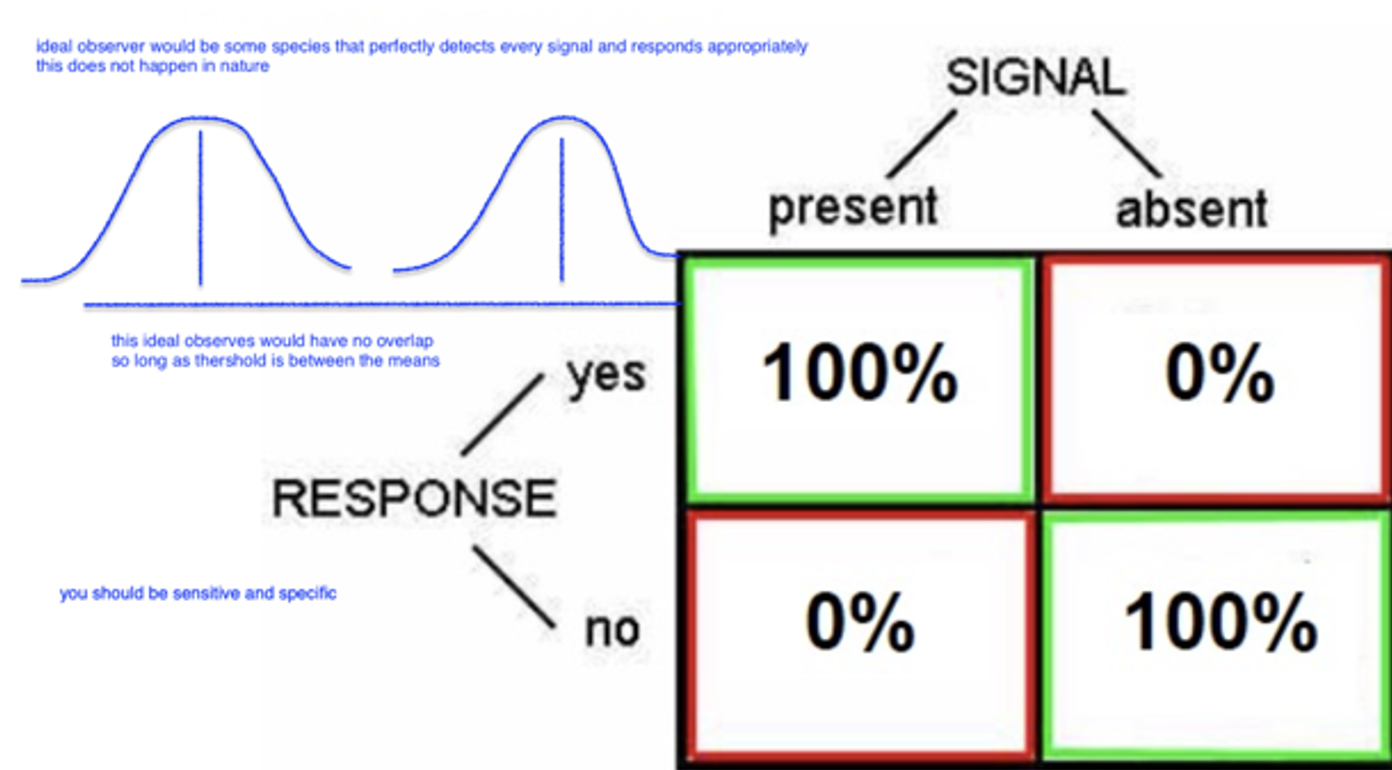
No sensory process with liberal bias

(costless behavior)

- ex. you are deaf in an island with lots of predators so should have a liberal bias (move threshold way to the left)

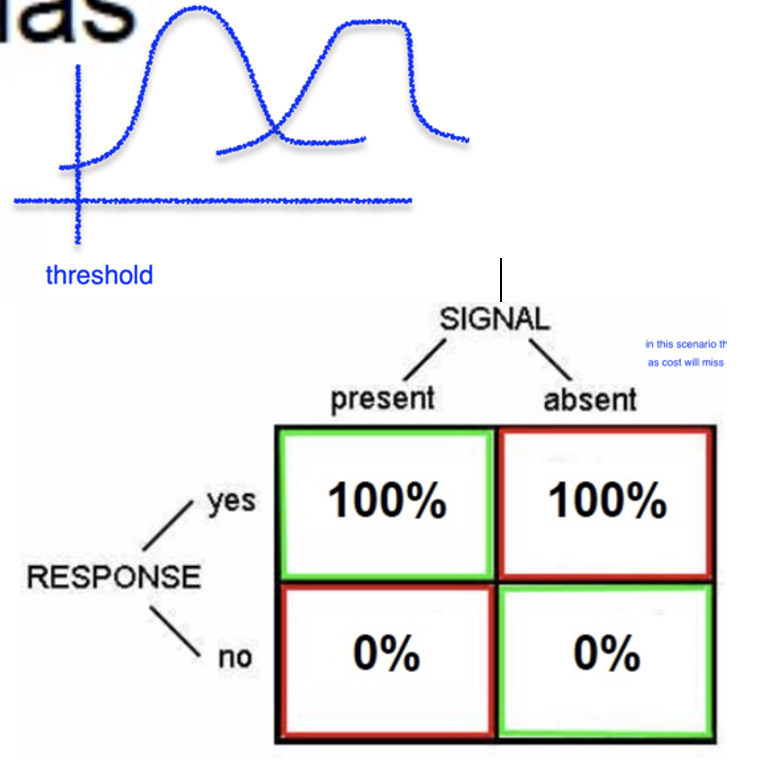
no sensory process with conservative bias

costly behaviour

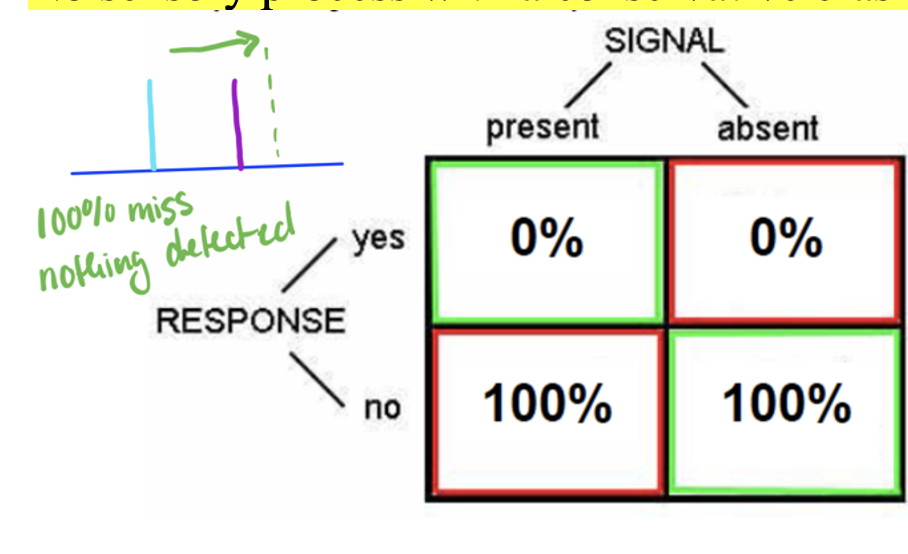
no sensory process, random agent

noise and signal overlap

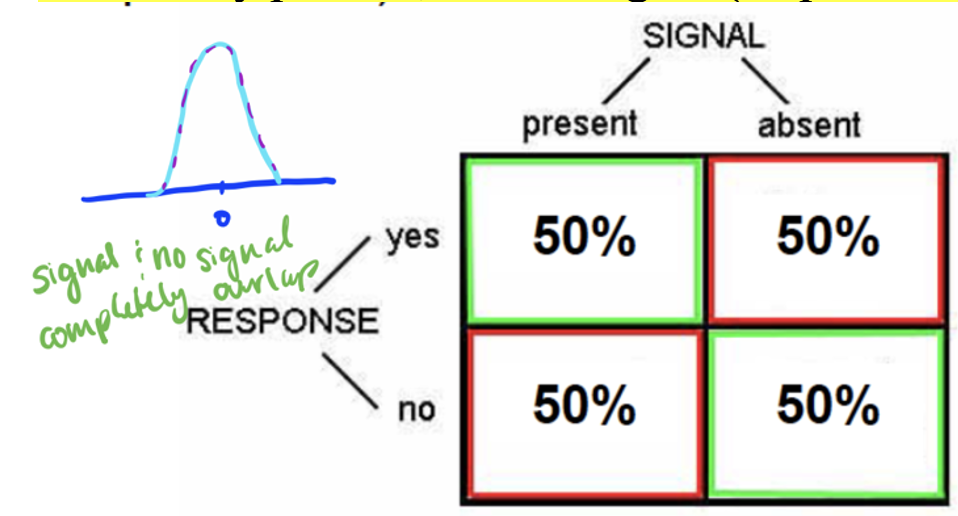
d’

d prime, sensitivity (distance between the two means)

d’ = z(Hits) - z(false alarms)

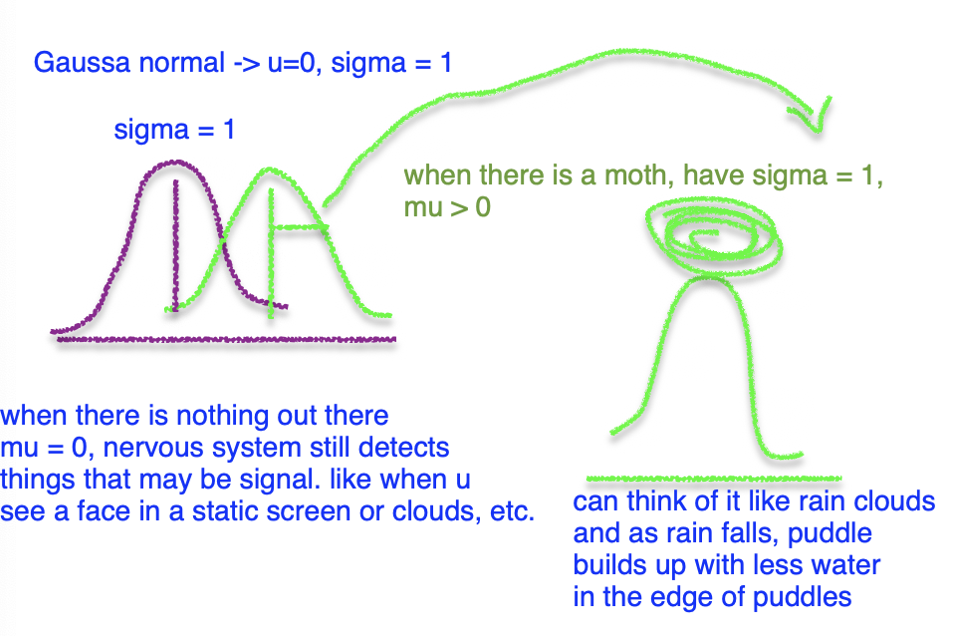
how to achieve perfect signal transduction

remove all exogenous noise, criterion between noise and signal

do not see it in nature because nature comes with noise, any decision an animal makes does so with uncertainty

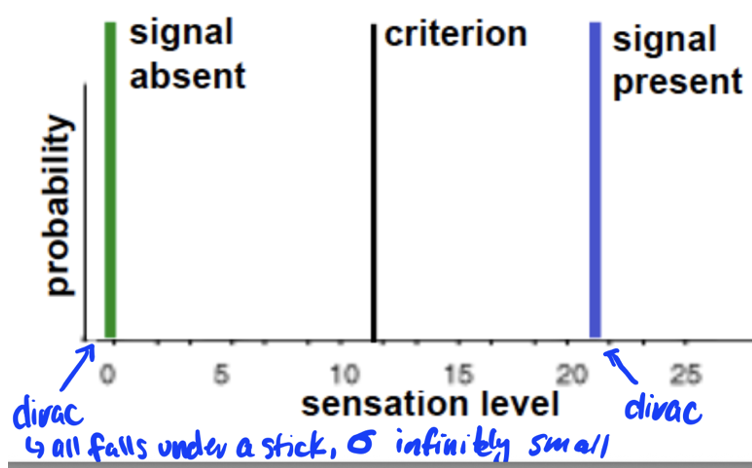
dirac

entire distribution falls under a stick, sigma infinitely small

Drift Diffusion Model (DDM)

• more evidence organism collects over time, more accurate its decision becomes over time

• Individual accumulates evidence over time until threshold is met

• like dust particle in air is bouncing around because it hits other particles in the air, more molecules means more hit rate look at diffusion and trajectory of dust particle, we see inverted Gaussian distributions

• if we blow air upwards to particle, it moves upward as well, introducing a current to particle, now behaves like this as a function of time

DDM change in location

signal + normal distribution of random noise with mean 0

dx = S dt + norm(0,1)

Leaky Competing Accumulators (LCA’s)

• population of neurons represent signals

• both inhibiting each other and are leaking, one who wins is one who gets more noise but noise is slow

• noise is what determines winner