i hate math save me

arcsin restriction of range

[-π/2, π/2]

arccos restriction of range

[0, π]

arctan restriction of range

(-π/2, π/2)

arccsc restriction of range

[-π/2, π/2] except 0

arcsec restriction of range

[-π/2, π/2] except 0

arccot restriction of range

[-π/2, π/2] except π/2

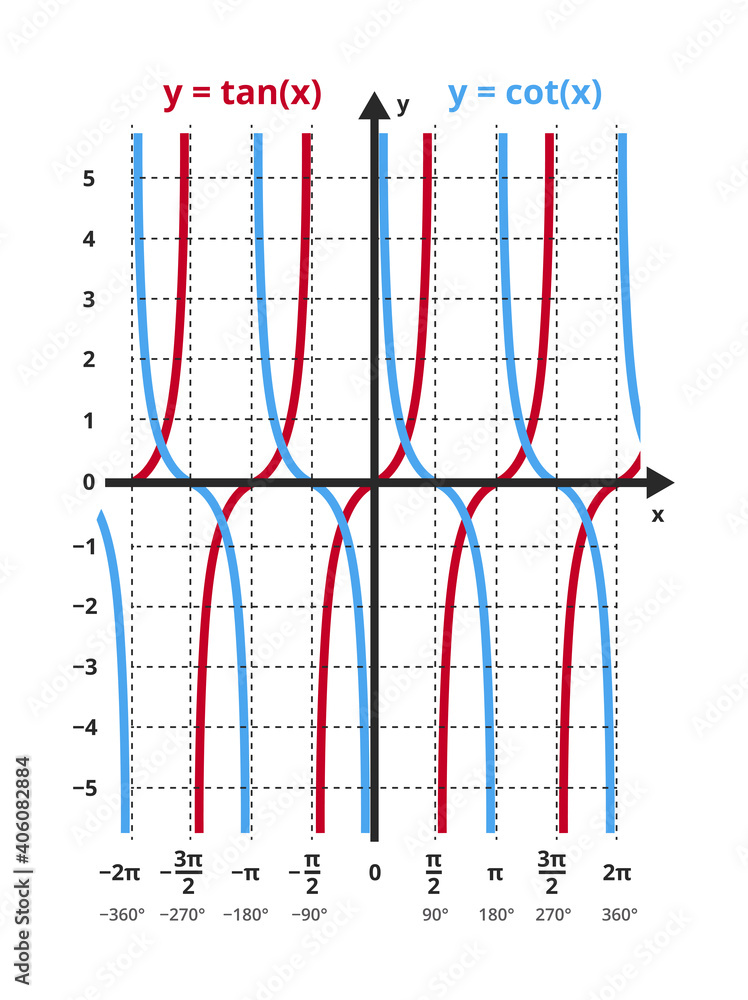
y=tanx vs. y=cotx

The functions y=tanx and y=cotx are reciprocal trigonometric functions; tanx is defined for all real numbers except odd multiples of π/2, while cotx is defined for all real numbers except integer multiples of π.

formula to convert radians to degrees

radians/π = degrees/180

half angle identity → cos²x=

cos²x = ½ + ½ cos (2x)

half angle identity → sin²x=

sin²x = ½ - ½ cos (2x)

double angle identity → cos2u =

cos 2u = cos²u - sin²u = -2sin²u+1 = 2cos²u-1

double angle identity → sin 2u =

sin 2u = 2 sin cosu

double angle identity → tan 2u =

(2 tan u)/(1-tan²u)

compound angle identity → sin (x±y) =

sin x cos y ± cos x sin y

cos (x±y) =

cos x cos y ∓ sin x sin y

tan (x±y)=

tan x ± tan y / 1 ∓ tan x tan y

terminal side

side that determines the angle

coterminal angles

angles that have same terminal side (210° and -150°)

period formula

2π/b = period

y=sin(1/2x) would stretch by ___

scale factor of 2

sin²x+cos²x=?

1

sin(90°-x) =

cosx

cscx

1/sinx

1/cosx

secx

1/tanx

cotx

sin(90-x)

cosx

cos(90-x)

sinx

tan(90-x)

cotx

sec(90-x)

cscx

csc(90-x)

secx

odd trig function identities

-(sinx)=sin(-x)

-(cscx)=csc(-x)

-(tanx)=tan(-x)

-(cotx)=cot(-x)

even trig function identities

cosx=cos(-x)

secx=sec(-x)

even function

y=x²

y=x^6+1

y=x²-2

odd function

y=x²+x

y=2x

even function properties

symetrical over y-axis

even number of exponents

f(-x)=f(x)

odd function properties

rotation of 180° about origin

odd number of exponents

f(-x) = -f(x)