Inorganic ACS

Nuclide

Type of atom with atomic number Z, equal to number of protons in nucleus (and electrons, since atom is neutral)

Mass number

A = the number of protons and neutrons in nucleus

Number of neutrons in an atom

A (mass number) - Z (atomic number)

Isotope

atom of an element that differ only by the number of neutrons (mass)

Monotopic

one natural nuclide

Relative atomic mass from abundance (Ar)

= (( %/100 ) * (accurate mass)) + ““…

Isotopes of an element have the same BLANK, but different BLANK

atomic number Z, atomic masses

ΔE = (in terms of frequency)

hv

Units of E

J, Joules

Units of v (frequency)

s^-1 or Hz

c (speed of light)

= λv

units of λ

m (meters)

ΔE = (in terms of wavelength)

hc/λ

ṽ = (in terms of wavelength)

1/λ

ṽ = (in terms of n)

R((1/n² )-(1/n’ ² ))

R (Rydberg constant) for Hydrogen

= 1.097e7 m^-1 or 1.097e5 cm^-1

n (principal quantum #) =

mvr/(h/2pi) (where m = mass of electron, v = velocity of electron, r = radius of orbit)

r_n (electron orbit radius)

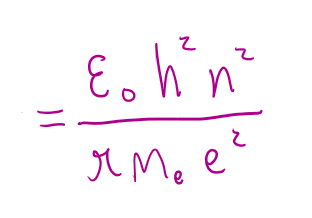
ε₀ (permittivity of a vacuum)

= 8.854e-12 Fm^-1

e (elementary charge on an electron)

= 1.602e-19 C

Ionization in terms of n

n=1 → n = ∞

Units of IE (ionization energy)

per mol of atoms

IE =

E∞ - E₁ = hc/λ

Ionization energy of Hydrogen

1312 kJ mol^-1 or 13.6 eV

λ (in terms of particles)

= h/mv (m = mass of particle, v = velocity of particle)

1eV

= 96.4853 kJ mol^-1

possible values of principal quantum number

1<=n<=∞

l (orbital quantum number)

determines shape of orbital and angular momentum

possible values of l

0,1,2…(n-1)

m_l (magnetic quantum number)

determines orientation of orbital

possible values of m_l

between +l and -l

For a 1s orbital, what is n

1

For a 1s orbital what is l

0

For a 1s orbital what is m_l

0

for a 1s orbital what is the radial part of the wavefunction R(r)

2e^-r

for a 1s orbital what is the angular part of the wavefunction A(θ,Φ)

1/(2sq(pi))

for a 2s orbital what is n

2

for a 2s orbital what is l

0

for a 2s orbital what is m_l

0

for a 2s orbital what is the radial part of the wavefunction R(r)

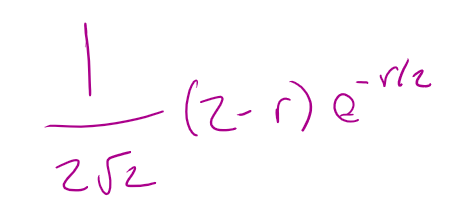
for a 2s orbital what is the angular part of the wavefunction A(θ,Φ)

1/(2sq(pi))

for a 2p_x orbital what is n

2

for a 2p_x orbital what is l

1

for a 2p_x orbital what is m_l

+1

for a 2p_x orbital what is the radial part of the wavefunction R(r)

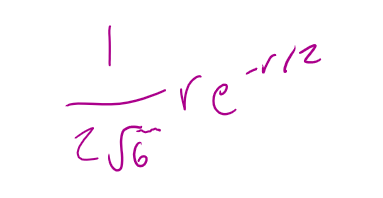
for a 2p_x orbital what is the angular part of the wavefunction A(θ,Φ)

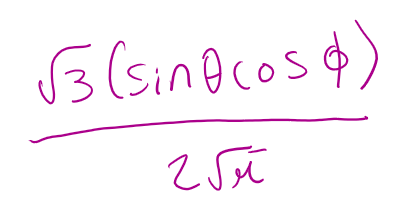
for a 2p_z orbital what is n

2

for a 2p_z orbital what is l

1

for a 2p_z orbital what is m_l

0

for a 2p_z orbital what is the radial part of the wavefunction R(r)

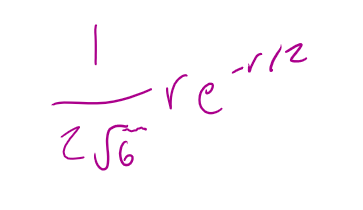
for a 2p_z orbital what is the angular part of the wavefunction A(θ,Φ)

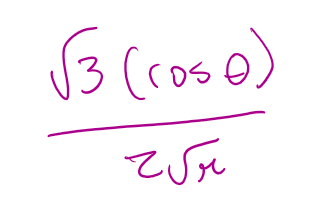
for a 2p_y orbital what is n

2

for a 2p_y orbital what is l

1

for a 2p_y orbital what is m_l

-1

for a 2p_y orbital what is the radial part of the wavefunction R(r)

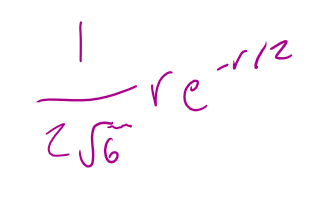
for a 2p_y orbital what is the angular part of the wavefunction A(θ,Φ)

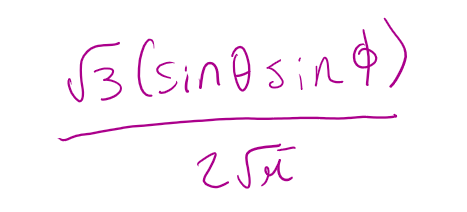
degenerate orbitals possess the same

energy

For a given value of n (n greater than or equal to 1) there is

1 s atomic orbital

For a given value of n (n greater than or equal to 2) there is

3 p atomic orbitals

For a given value of n (n greater than or equal to 3) there is

5 d atomic orbitals

For a given value of n (n greater than or equal to 4) there is

7 f atomic orbitals

likelihood of an electron being further from the nucleus

increases as n increases (not linearly)

s atomic orbitals have a finite value of

R(r) at the nucleus

for all orbitals other than s

R(r) = 0 at the nucleus

for the 1s orbital

R(r) is always positive

for the first orbital of all other orbital types besides 1s (ie. 2p, 3d, 4f)

R(r) is positive everywhere except at the origin

for the second orbital of a given type (ie. 2s, 3p, 4d, 5f)

R(r) may be positive or negative but the wavefunction has only one sign change

the point at which R(r)=0 (not including the origin) is called

a radial node

for the third orbital of a given type (ie. 3s, 4p, 5d, 6f)

R(r) has two sign changes (it possesses two radial nodes)

ns orbitals have BLANK radial nodes

(n-1)

np orbitals have BLANK radial nodes

(n-2)

nd orbitals have BLANK radial nodes

(n-3)

nf orbitals have BLANK radial nodes

(n-4)

Radial distribution

=4pir²R(r)²

Using the radial distribution function, disregarding r=0, what points correspond to radial nodes?

Anywhere 4pir²R(r)²=0

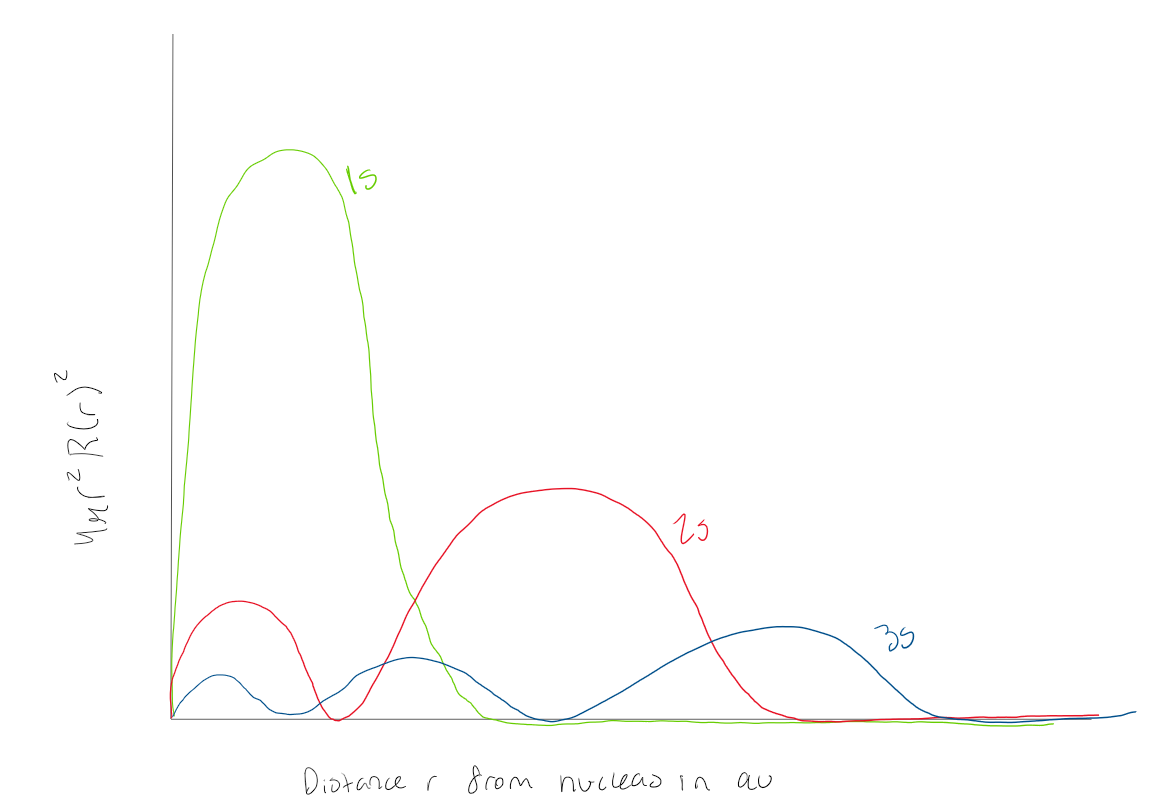
Using the graph, how many radial nodes does a 1s orbital have

0 radial nodes

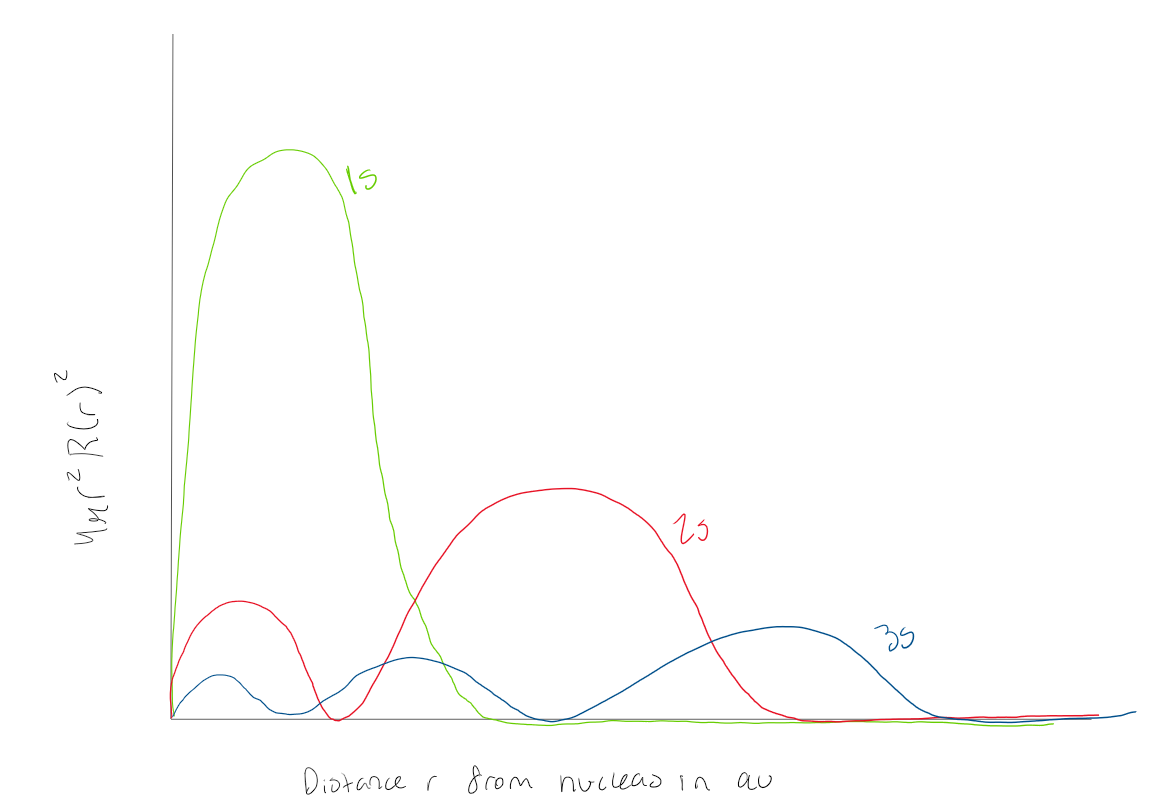
Using the graph, how many radial nodes does a 2s orbital have

1 radial node

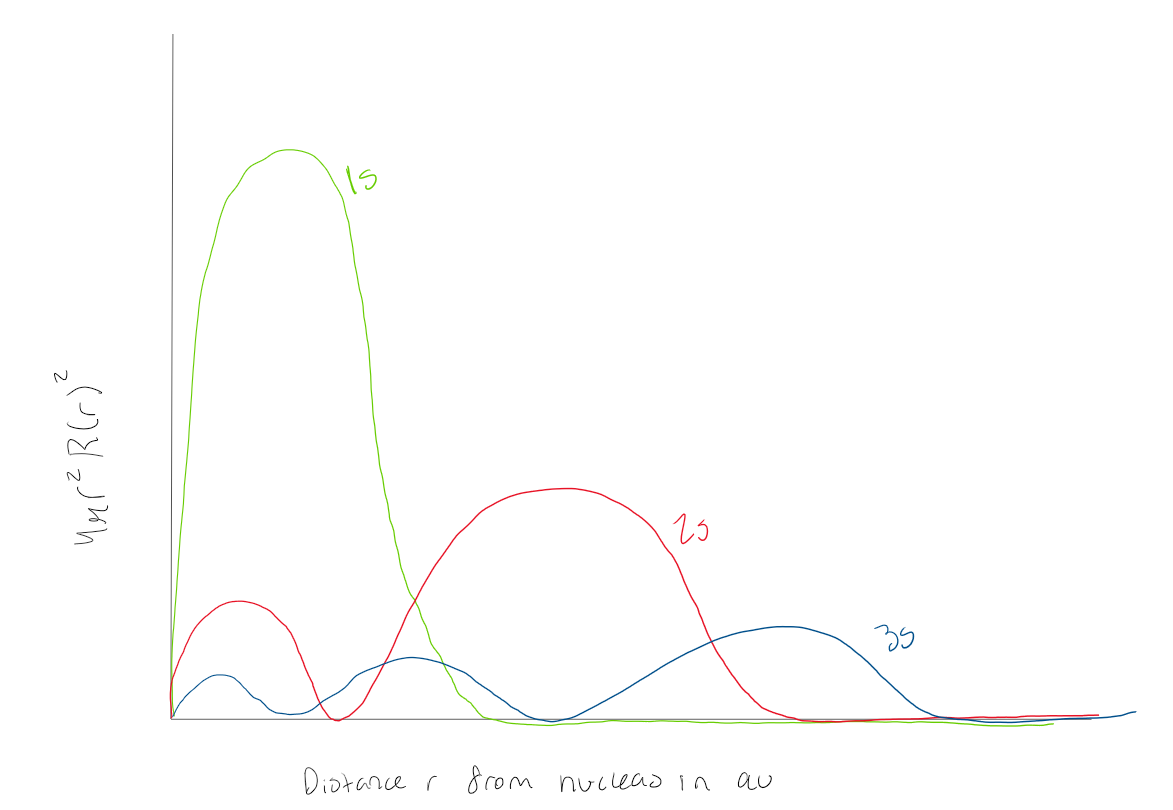
Using the graph how many radial nodes does a 3s atomic orbital have?

2 radial nodes

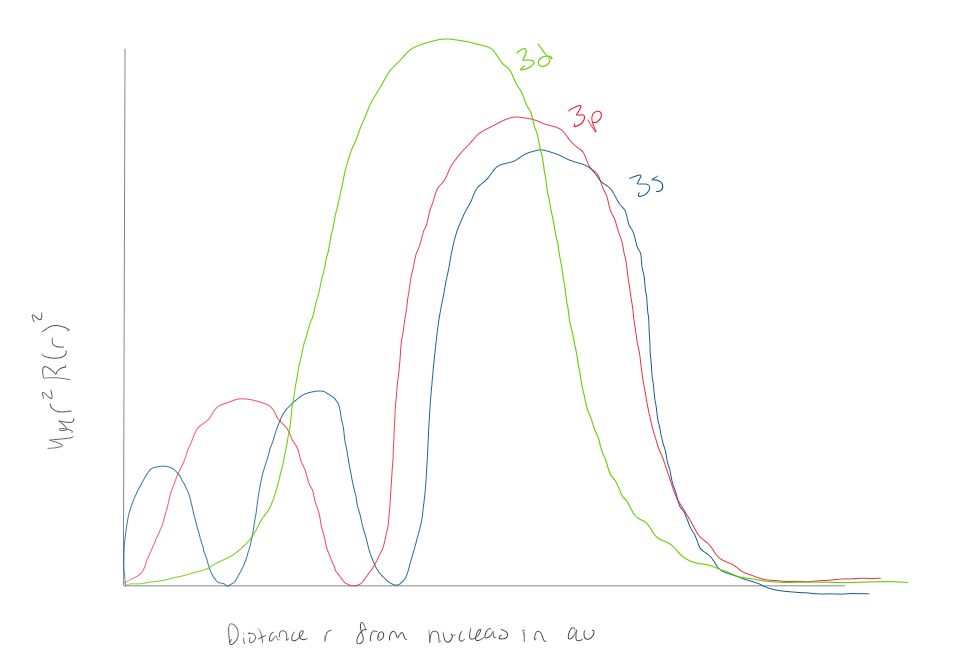
Using the graph how many radial nodes does a 3d orbital have?

0 radial nodes

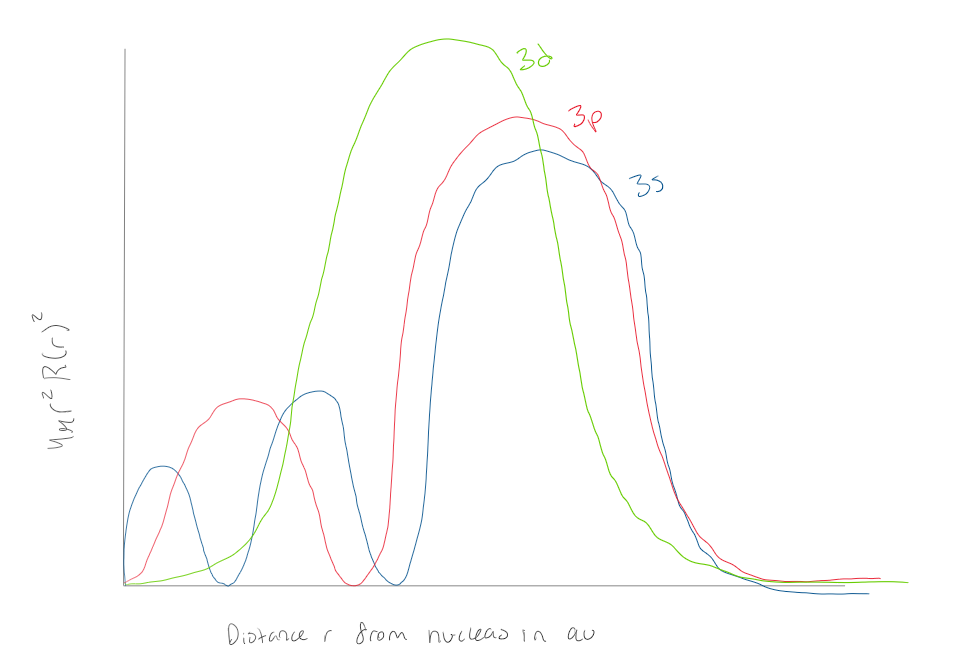
Using the graph, how many radial nodes does a 3p orbital have?

1 radial node

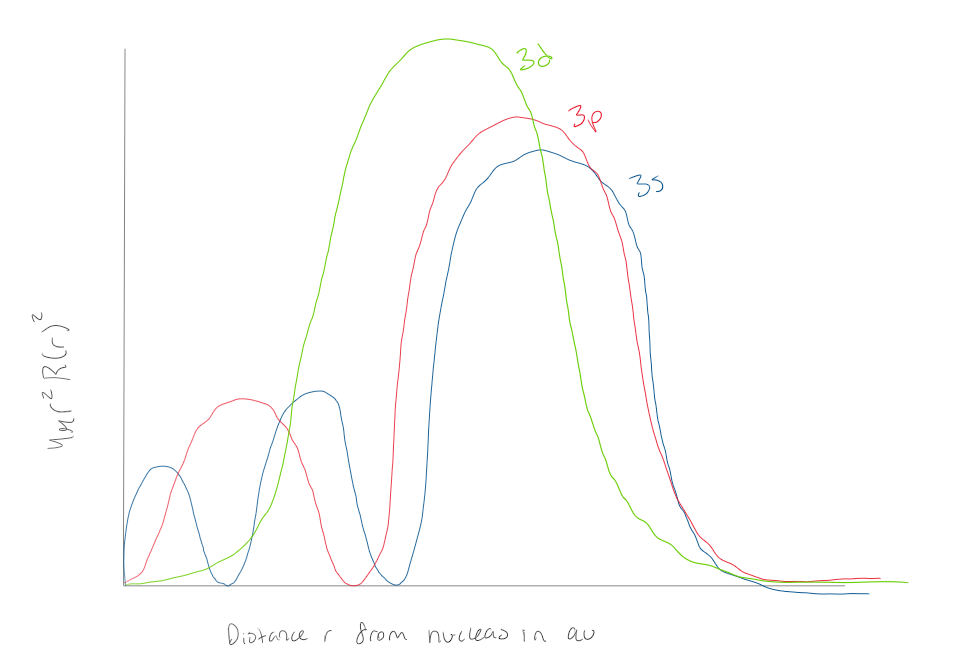
Using the graph how many radial nodes does a 3s orbital have?

2

The angular part of the wavefunction A(θ,Φ) is independent of

n

For s orbitals, A(θ,Φ) is independent of

θ and Φ

E (orbital energies) =

-(kZ²)/n² (where Z = atomic number and k = hcR = 1.312e3 kJ mol^-1)

Orbital energy levels get closer as

n increases

The larger the n the larger the

size of the orbital

And increase in orbital size corresponds to an increase in

an orbital being more diffuse

S (spin quantum number) =

1/2

m_s (magnetic spin quantum number) =

± 1/2

Orbital angular momentum =

Sqrt(l(l+1))*(h/2pi)

spin angular momentum =

Sqrt(s(s+1))*(h/2pi)

total angular momentum =

Sqrt(j(j+1))*(h/2pi)

j (inner quantum number) =

|l+s| or |l-s|

In a multi-electron atom, orbitals with the same value of n but different values of l are

NOT degenerate

The IE of noble gases are

high

IE of group one elements are

low

IE increases

across a period

IE is similar for

a given row of d block elements

EA =

-ΔU (at 0K)

Adding an electron to an atom is typically

exothermic