Physics OCR A-level: Gravitational fields

• Gravitational field

A field created around any object with mass, extending all the way to infinity, but diminishing as the distance form the centre of mass of the object increases

• Gravitational field strength, g

The gravitational force exerted per unit mass at a point within a gravitational field. (units NKg^-1 or ms^-2)

• Gravitational field lines

lines of force used to map the gravitational field pattern around an object having mass

Radial field

A symmetrical field than diminishes with distance² from its centre, such as the gravitational field around a spherical mass or the electrical field around a spherical charged object

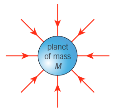
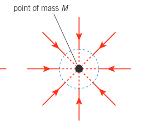
Point mass

A mass with negligible volume

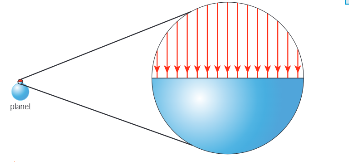
Uniform gravitational field

A gravitational field in which the field lines are parallel and the value for g remains constant

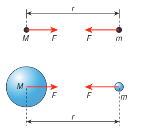
Newton’s law of gravitation

The force between two point masses is directly proportional to the product of the masses and inversely proportional to the square of the separation between the centres

F=\frac{-GMm}{r^2}

• Gravitational constant, G

The constant in Newton’s law of gravitation With value: 6.67×10^-11NKg^-2m²

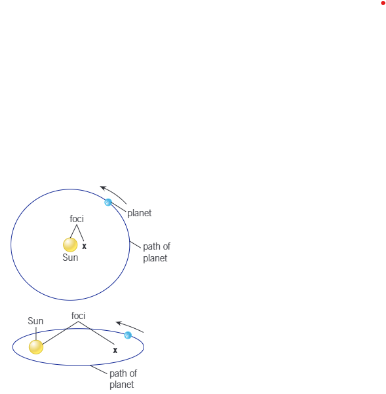
• Kepler’s first law of planetary motion

The orbit of a planet is an ellipse with the Sun at one of the two foci

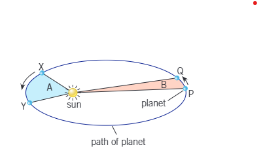
• Kepler’s second laws of planetary motion

A line segment connecting a planet to the Sun sweeps out equal areas during equal time intervals.

• Kepler’s third laws of planetary motion

The square of the orbital period T of a planet is directly proportional to the cube of its average distance r from the sun

\frac{T^2}{r^3}=k or T^2=\left(\frac{4\pi^2}{GM}\right)r^3

Kepler’s third law derived

• centripetal force on planet = Gravitational force on planet\frac{mv^2}{r}=\frac{GMm}{r^2} or v^2=\frac{GM}{r}

• since moving in circular motion speed can be determined using v=\frac{2\pi r}{T}

• substitute this in to give \frac{4\pi^2r^2}{T^2}=\frac{GM}{r}

• rearrange to give T^2=\left(\frac{4\pi^2}{GM}\right)r^3