math mistakes

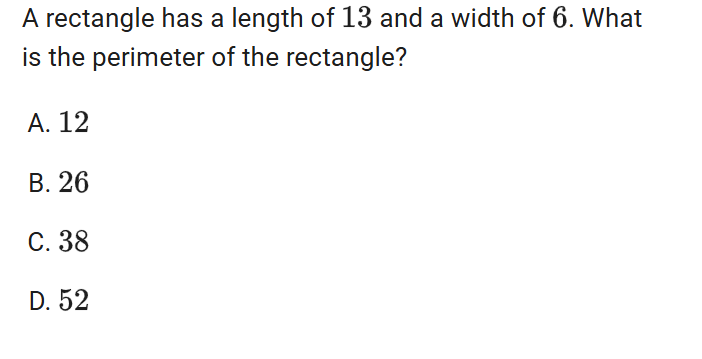
area and volume

the perimeter for a rectangle is 2 times the length plus the with
the perimeter for a square is 4 times the side lengths
for a triangle its side1+side2+side3

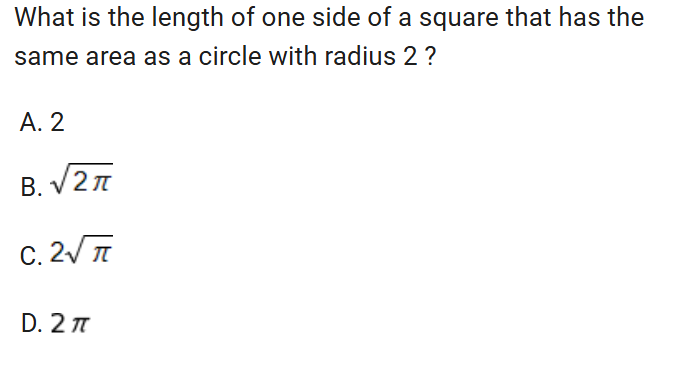
area and volume

if you get an answer with a square root like 2pie square root you have to split the square roots up and solve it

area and volume

the volume equation for a rectangular prism is (L)(W)(H) don’t mistake it for a rectangular pyramid which is 1/2(L)(W)(H)

area and volume

since the circumfrence is 2 times pie radius and since the diameter is 2 times the radius the circumfrence is the same as the diameter.

Area and volume

first you find the volume of the whole can by multiplying the area of the base of the can times the height given then subtract the volume of the syrup to get the volume of the fruit

You can use ether formula just use this one because we were given the base area

area and volume

first place the 473 in the equation for volume
then multiply 48 on both sides(don’t multiply them together yet)
then to get rid of the 7 pie we divide it on both sides to isolate K³
then we must cube root the equation on both sides to get the answer

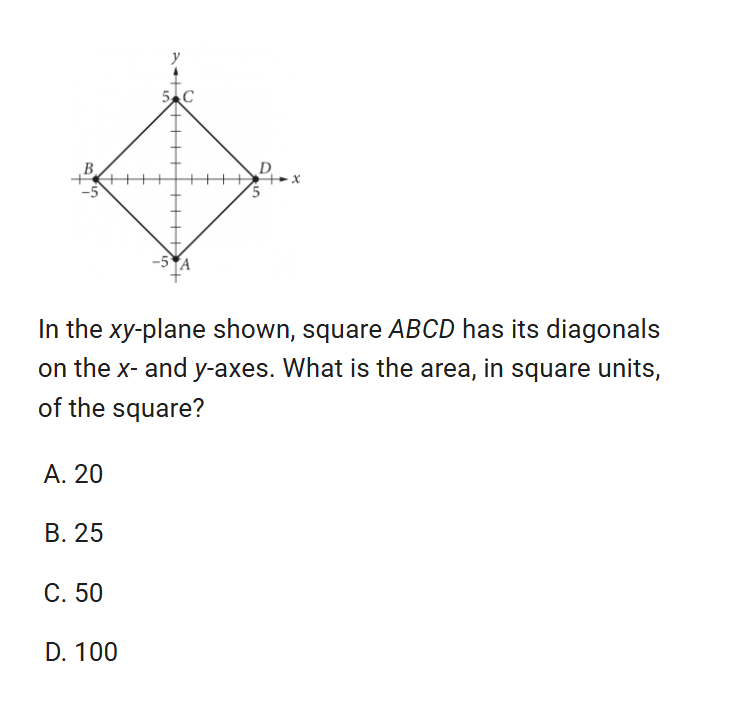
area and volume

when given a problem like this try to find other shapes you can use to find what your looking for.

in the shape you have 4 of the same triangles that all of the same side lengths and adjacent lengths. use the area of a triangle formula A=1/2bh then multiply that answer by 4.

area and volume

I didn’t understand how to express the 4 inches longer than the radius sentence.
ex: the cylindrical container formula when given the height is A= pie r^2 times H so when it says the height is 4 inches longer than the radius express it as (r+4) then distribute the pie r² into the whole thing.

area and volume

Made the mistake of multiplying 1.20 by 2
-since each of the sides are increased by 20% it can be arranged like this (1.20 × Length) × (1.20 × Width) or (1.20 × 1.20) × (Length × Width) because the length and width would be the area you add the 360 in there and multiply the 1.20 together.

I didn’t divide 1/3 properly on desmos. when dividing two fractions you write the fraction then click to the side of it then hit divide and then enter the fraction.

after dividing the fraction you divide by 9 then square root and because you can’t have a negative value for square root for radius that leaves the positive number.

area and volume

i accidently put 22 inside the volume and didn’t arrange the problem correctly
first know the volume equation of a circular cylinder is v= pie r² times h so you put the numbers in while keeping the variables h and r because we don’t know their exact values. and it becomes 2 pie r² times h so multiply the original volume by 2.

how to know when to use just the variables/relationships vs plugging them in:
questions: If the question is a "what if we change this?" type, use relationships.
questions about a single, fully described object: Plug and calculate directly.

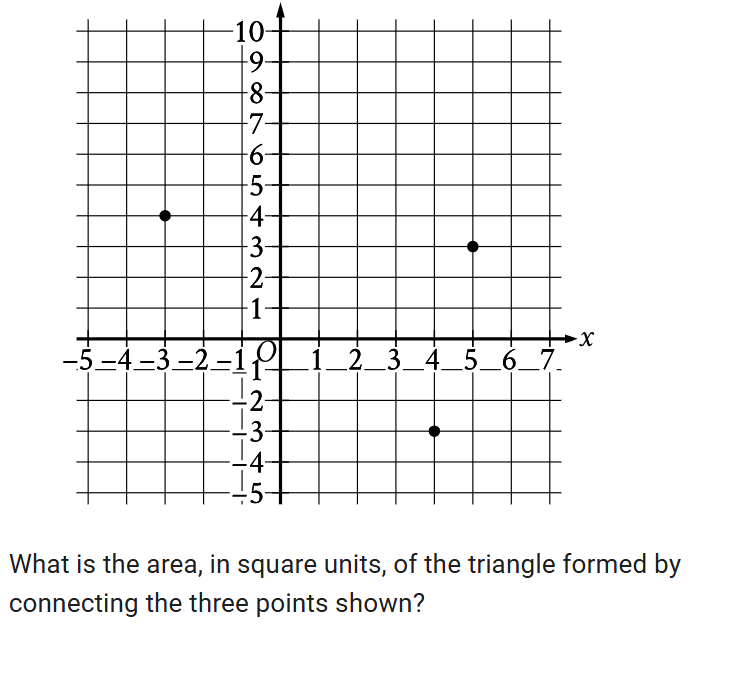
area and volume

For a shaded region problem like this its best to use other shapes that you can make to solve the problem

first trace it into a triangle then ralize the triangle is a part of a rectangle. then find the area of the rectangle. then section the square into 3 triangels then find the area for them then subtract those areas from the rectangle

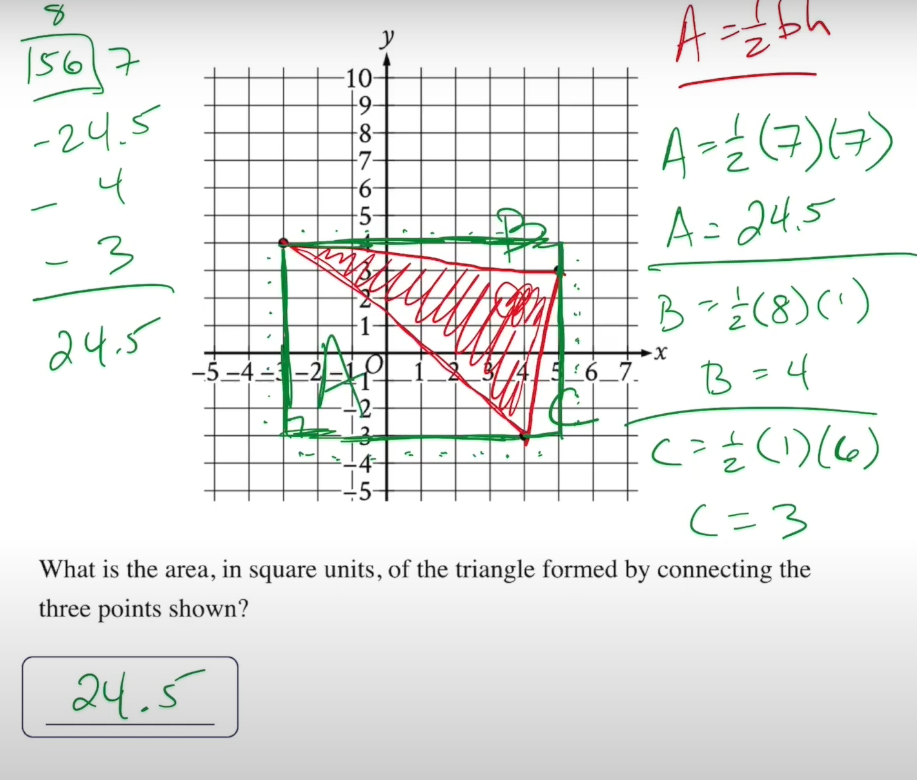
area and volume

I didn’t know how to calculate surface area of a rectangular prism
the surface area equation is 2(Lw+Lh+wh)

area and volume

i didn’t understand scale factor and when the problem says a similar shape is blank bigger than another shape it means this Length (1 dimension): Scales by k

• Area (2 dimensions): Scales by k2

• Volume (3 dimensions): Scales by k3
  
  plug in 4 for k² since its two dimensions and its 16 times the area of abc which you can represent by 16a then divide 16 from 270

area and volume

i didn’t know the surface area equation or the volume of a cube equation. The surface area equation is 6s² and the volume of a cube is s³
so write out the equation as s=6s² since the surface area is 54 than it can be 54=6s² divide then square root and then plug that number into the volume formula s³

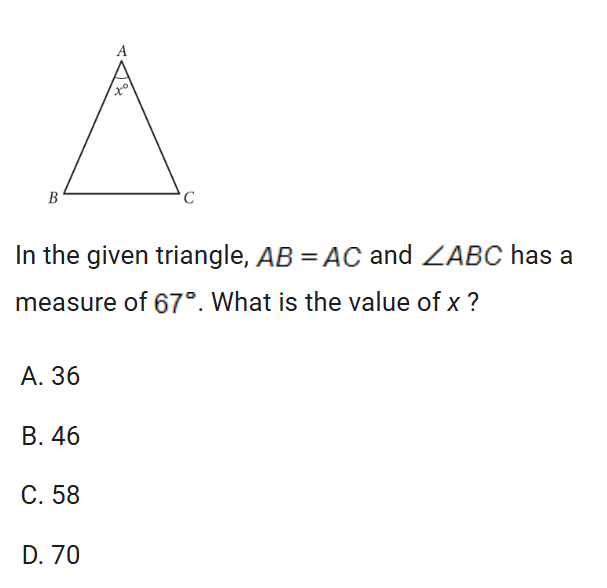
lines angles and triangles

The common letter A tells you which angle is the one their talking about. so angle b is the same as angle c.

lines and angles and triangles

i focused on the blank angles instead of solving for Z if your given the two angles you can solve for the other angle.

lines and angles and triangles

use alternate interior angles then minus 64 by 180 to get a.

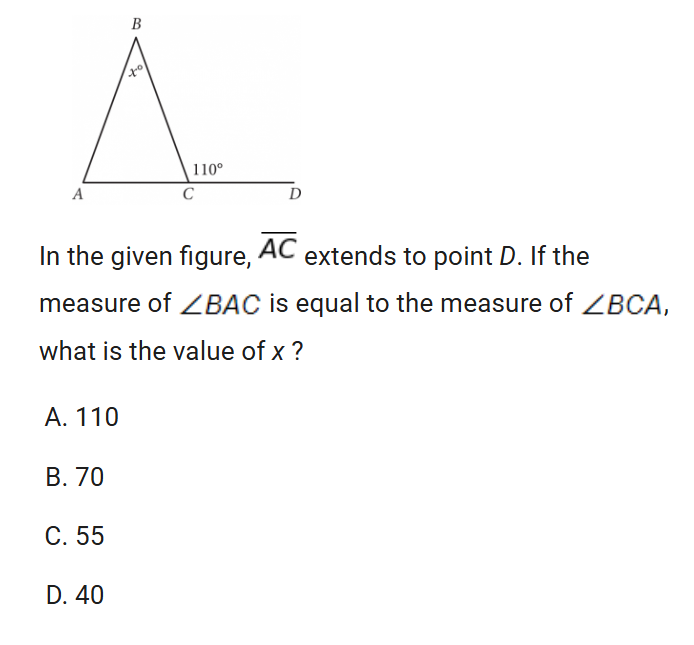
lines angles and triangles

i made the mistake of thinking the outside angle is angle c. You subtract 110 form 180 to get angle c. and since a and c are equal they are the same. then you solve.

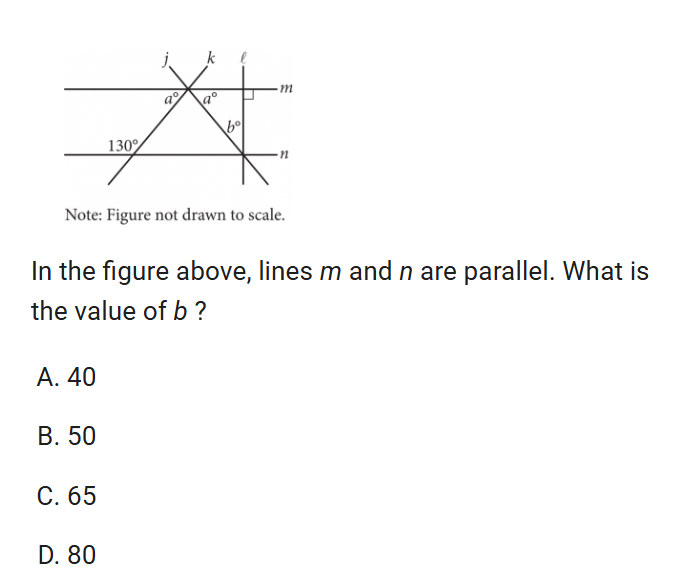
Lines angles and triangles

i tried to use 130 behind b angle, which doesn’t work because they are seperated by 2 lines.

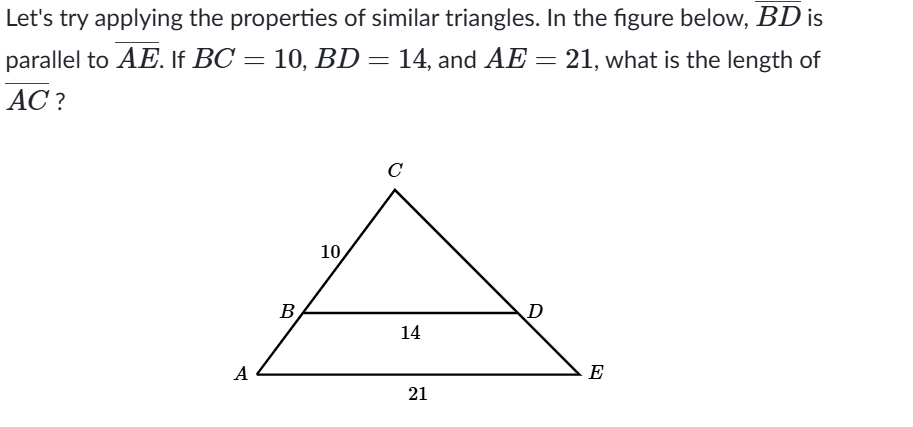
Lines angles and triangles

I didn’t know how to write the congruency correctly. When writing the problem you have to make sure it goes in order of congruence. (multiple ways can be correct.

also made the mistake of thinking CA which is AC in this, i added it together with BC when its the whole thing

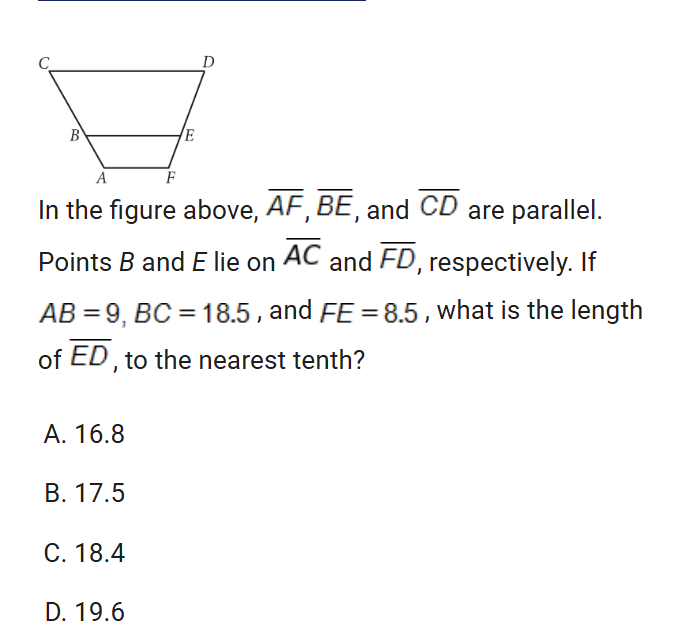
Lines angles and triangles

i didn’t know the parallel proportionality theorem. you use the theorem when you have: three or more parallel lines and the parallel lines are intersected by two or more transversals(lines that cross the parallel lines but aren’t parallel. like the image for an example.)

when writing out the proportion using the theorem you write the corresponding segments not the lengths.
AB/BC-FE/ED

lines angles and triangles

I didn’t use the angles given or did i solve for the missing angels to realize the triangles were the same and found the ratio accordingly. you should always solve for the missing angle.

I realized an isosceles triangle must have two equal angle measures but I just picked a random number. You have to solve each one to see if you will get the same angle measure for each.

like 65+50-180 will give you 65 which if you chose the answer choice B you will have the same angle measure for 2 of the angles.

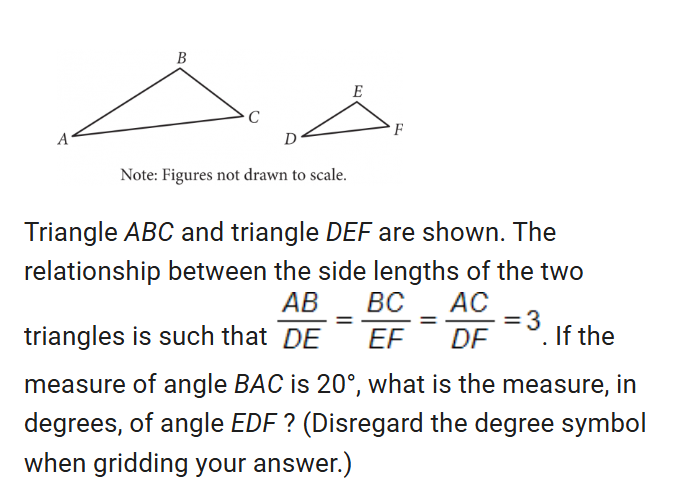
lines angles and triangles.

Watch out: when the problem says figure not drawn to scale or says nothing don’t assume its half or double of anything. But if it says figure drawn to scale then you can presume that.

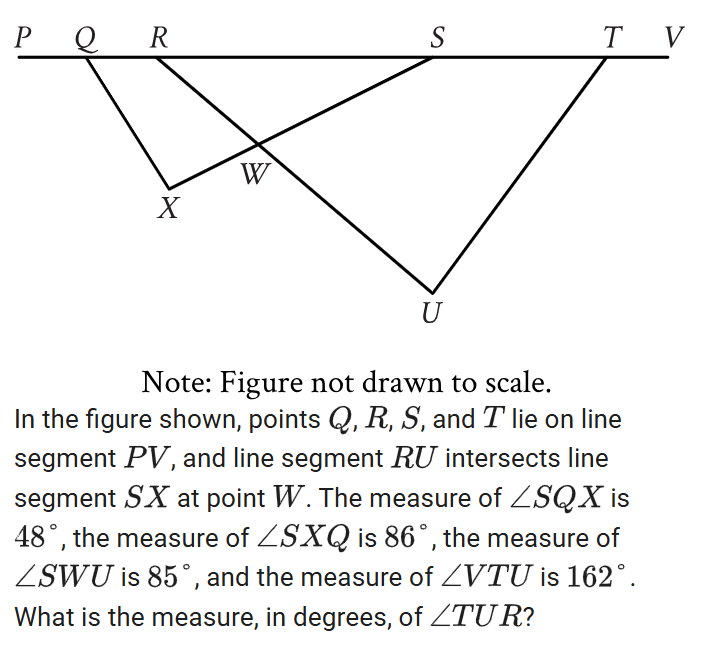
Lines angles and triangles

I made the mistake of not solving for the supplementary angles. i was focused too much on the end goal. you have to draw these out and solve for the supplementary angles and then you can fill in the missing pieces.

Also as a trick instead of figuring it out with the triangle you can use the quadrilateral trick shown in the picture.

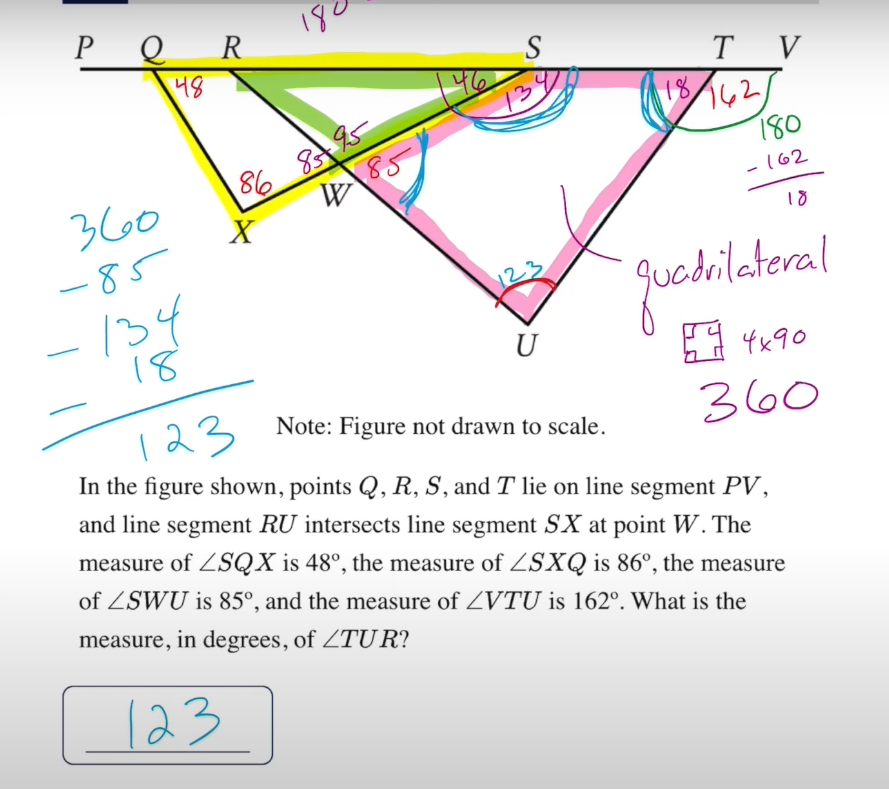
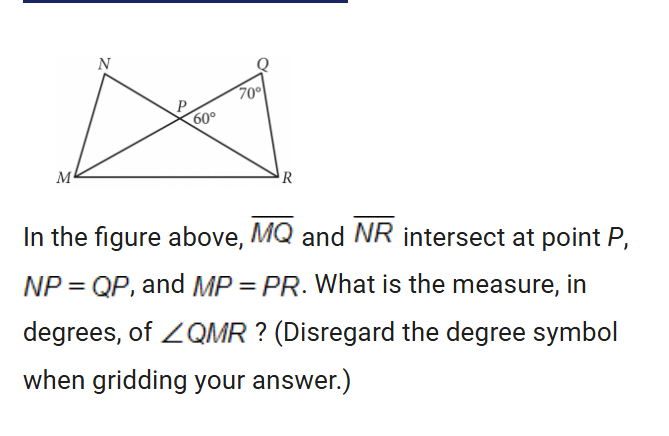
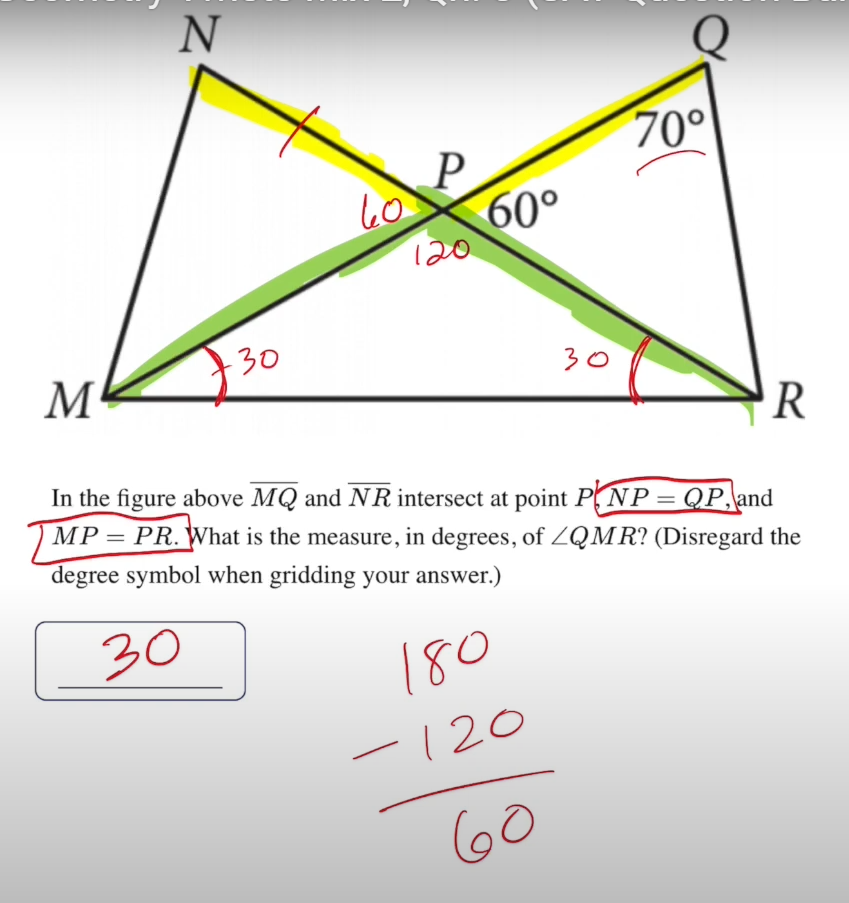
Lines angles and triangles

since they tell us mp=pr they have the same length so mpr is an isosceles triangle. and since we get 120 by the supplementary angle on top by subtracting 60-180 you can just do 180-120 and get 60. and since its isosceles two of the angles will be the same so divide 60 by 2 since they will both share that angle

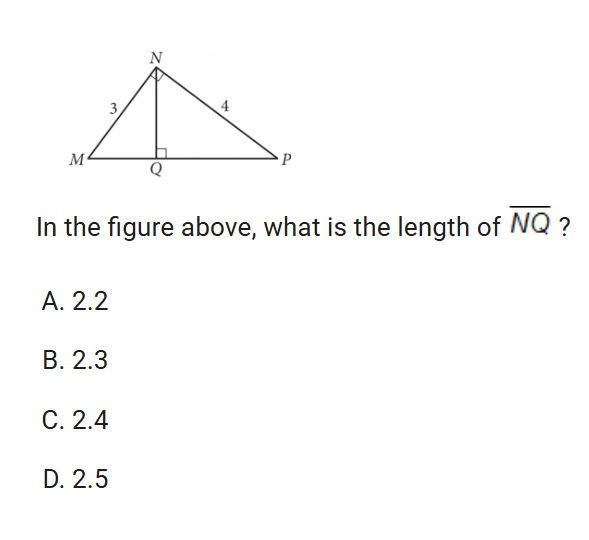
lines angles and triangles

i didn’t know how to prove a triangle was similar
one way is to see if they have three of the same angles or at least two since you can figure out the three one easily since they add to 180

lines angels and triangles

i didn’t know how to solve it past the Pythagorean theorem and i just didn’t know how to solve it

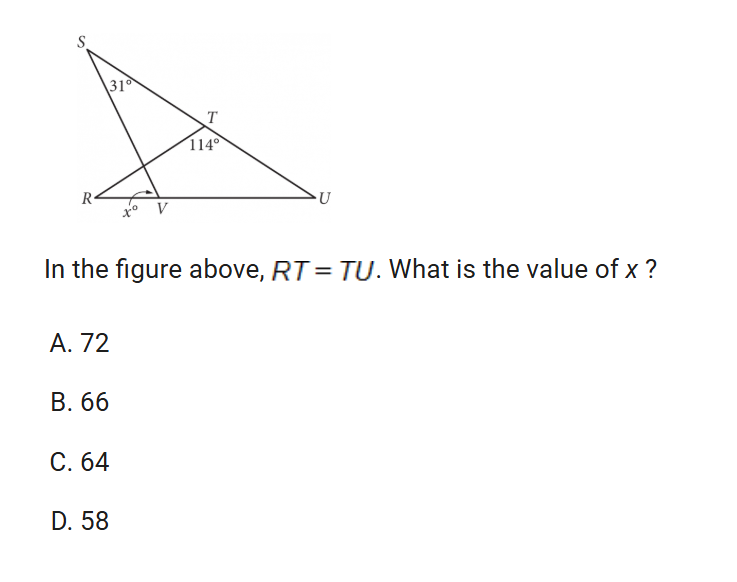
lines, angles, and triangles

caution never assume the whole thing is an isosceles so just solve 144 for a supplementary angle for t then find the missing angle

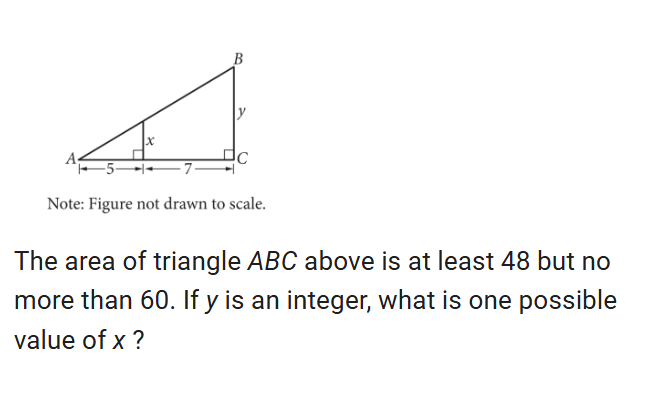
Lines angles and triangles

i got it wrong because i didn’t use the area formula to solve for the whole triangles y equation.

after that you get 6y as the area. since it says the area is between 48 and 60 you set it as an inequality.

then you set up the proportion smaller height/large height=small base/large base or small base/small height = large base/small height

then once you get the proportion you plug in the possible values for y which we solved for 8-10 then simplify the fractions

Lines angles and triangles

i made the mistake of not realizing they are similar triangles.
how to realize they are similar triangles: 1. they share the same angle s and. 2.a line inside a triangle that is parallel to a side always creates a smaller, similar triangle.

then solve for the area and then write a proportion to get Ks then subtract ks by 22 to get TK

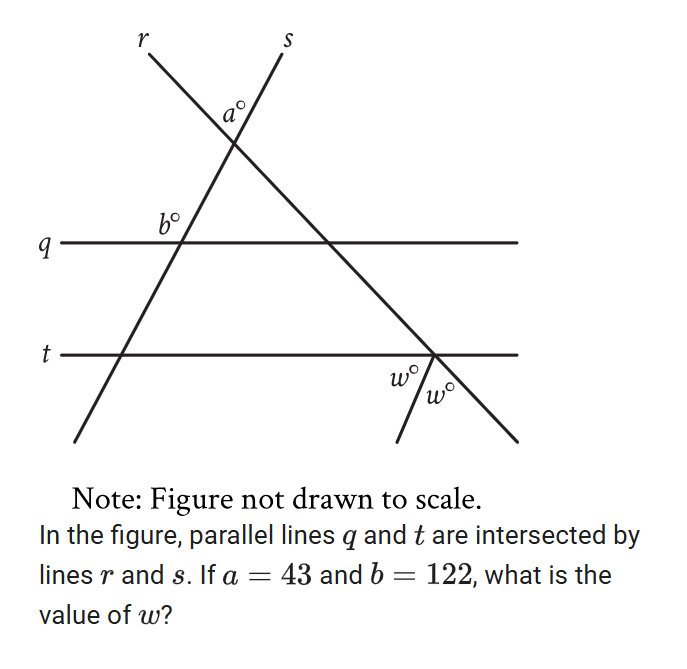
Lines angles and triangles

I got it wrong because 1. i didn’t know how to solve it efficiently I didn’t realize about the corresponding angles (angles on the same transversal that cuts through two parallel lines)

2. i didn’t know how to solve for W the correct way. once you realize its corresponding angles you also realize the two w’s equal to 180 because they fill up the rest of the line then you divide the answer by 2w because there’s two w’s.

Lines angles and triangles

I didn’t know the geometric mean theorem: a right triangle with a line in the middle called the altitude(alt) which separates them and creates a relationship like this a/alt=alt/b which you can use to solve for the legs.

use the thereom ONLY IF:
1. You have a right-angled triangle (a triangle with one 90-degree corner).

2. The altitude (the height) is drawn from that 90-degree corner to the longest side (the hypotenuse).