6.3 - Matrix Algebra

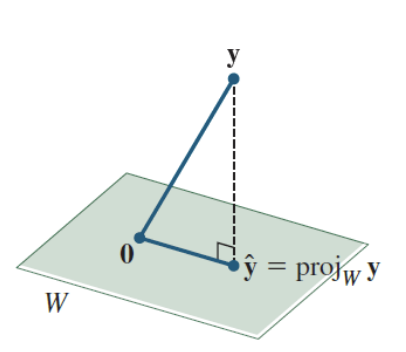
What is an orthogonal projection of y onto W?

The unique vector y(hat) ∈ W such that y−y(hat) is orthogonal to W and y(hat) is the closest vector in W to y.

Imagine shining a flashlight straight down onto a plane.

The shadow of y that lands on the plane is y(hat).

You’re forcing y onto W in the most direct (perpendicular) way.

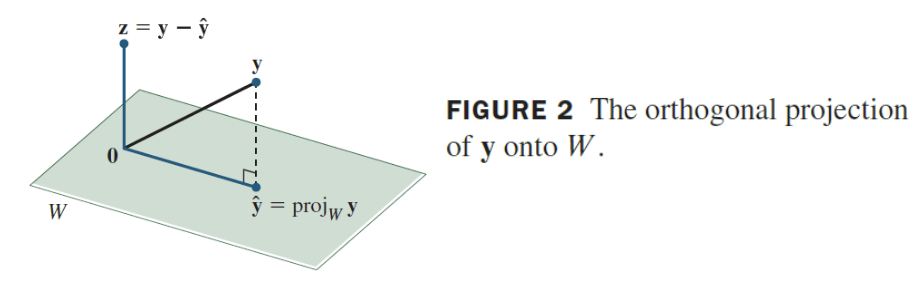
Orthogonal Decomposition Theorem statement?

Every vector y can be uniquely written as y = y(hat) + z, where y(hat) ∈ W and z ∈ W(perpendicular)

Every vectory can be split into:

1) the part that lives in the subspace (the shadow).

2) The part that sticks straight out of it.

Like splitting a force into horizontal + vertical components.

Formula for projection when {u1​,…,up​} is an orthogonal basis of W?

Picture

youre measuring how much of y points in each direction of the basis.

The dot product asks:

• How aligned is y with this basis vector.

You scale each basis vector by how strongly y points toward it.

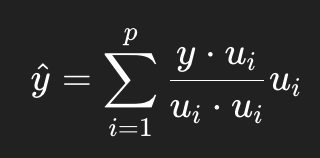
How do you compute the perpindicular component?

z = y - y(hat)

You’re literally subtracting the shadow from the original vector. Whats left is the part that didn’t land on the subspace.

Why is the decomposition y = y(hat) + z unique?

Because the only vector in both W and W(perpindicular) is 0.

A vector cant point both in a direction and be perfectly perpendicular to that direction unless its zero.

So the split is one of a kind.

If y is already in W, what is proj_Wy?

proj_Wy = y

If y is already in the plane / line, its shadow on the plane is just itself.

If y is in W(perpendicular), what is proj_Wy?

proj_Wy = 0

If y is sticking straight up from the plane, its shadow hits the origin. IT has zero components pointing along W

What does the Best Approximation Theorem say?

y(hat) = proj_Wy is the closest point in W to y. It minimizes ||y-v|| over all v ∈ W.

v being some vector.

The perpendicular drop to the subspace is the shortest distance.

Any other point in W is farther away because you’d have to move sideways too.

What is the distance from y to W

dist(y, W) = ||y - y(hat)|| = ||y - proj_Wy||

Distance from a point to a subspace = length of the leftover perpendicular piece.

Just like distance from a point to a line is the height of the perpendicular.

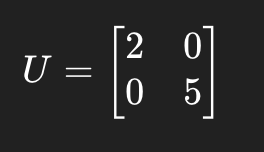
What is the matrix formula for projection when U has orthogonal columns?

U orthogonal columns = Each column vector in U is orthogonal to every other column. it doesnt require them to be unit vectors, just perpindicular

proj_Wy = UU^Ty

U^Ty tells you how much y lines up with each basis vector.

Multiplying back by U reconstructs the projected vector.

It’s:

1) measure alignment

2) Rebuild the shadow

What does U contain in the projection matrix formula?

Columns of U = orthogonal basis vectors u₁,…u_p.

Think of U as a stack of directions that span the subspace

The projection asks:

• How much of y lies in each of these directions.

Why does UU^Ty work for projection?

The projection is a linear combination of columns of U with weights U^Ty

Its like recording how much of a y points in each direction (using U^T)

then constructing the shadow using those amount (using U)

How do you check if your projection is correct?

Verify: (y - y(hat)) x u_i = 0 for all basis vectors u_i

The leftover part must stick straight out of the subspace. If not, the projection is wrong.

What must be true about the basis vectors to use the simple projection formula?

They must be orthogonal (not just linearly independent).

If the basis vectors point weird directions, projections overlap and interfere. Orthogonal basis vectors don’t mix with each other.

What changes if your basis isn’t orthogonal?

You must first apply Gram-Schmidt to make an orthogonal basis.

You must straighten out the basis so each direction is cleanly separate. Otherwise the projections wont isolate clean components.

WHen is the error minimized:

when v = y(hat)