Differential Equations Exam 1 Concepts

Purdue 266

First Order: Separable

Form: dy/dx = f(x) * g(y)

separate so x are on one side and y is on other, integrate and solve for y in terms of x

First Order: Linear

Form: A(x)y’ + B(x)y= C(x)

Method used: Integrating Factor Method

1. normalize (y’+P(x)y=Q(x)), get y’ by itself, so divide by its coefficient

2. mu = e^(S P(x),  mu is called the integrating factor

3. mu y = S mu  Q(x)   + C

4. solve for y

First Order: Exact Differential Equations

Form: M(x,y)dx + N(x,y) dy = 0

1. Test for exactness, My = Nx, so do a partial derivative of M with respect to y and N with respect to x

2. General solution for an exact equation is in the form F(x,y) = C

   1. To find this do: Fx = M and Fy = N, integrate this

   2. Assemble F by adding the DISTINCT terms from the integration step, so if there are two that are alike don’t add twice just put in once.

First Order: Bernoulli (Almost Linear)

Form: A(x)y’ + B(x)y= C(x)y^n n doesn’t equal 1,0

To solve:

1. Normalize, get the y’ to have coefficient of 1,

2. Then divide by y^n, and set v = the y component from B(x)y, to “fix” and make linear, then follow first order linear equation to solve and at the end replace back y for v, and solve for y by getting rid of any exponents.

First Order: Homogeneous (Almost separable)

Form: dy/dx=f(x,y)/g(x,y)    Degree of each term is the same

1. make sure each term has same degree, if there is xy that is degree two since x has degree 1 and y has degree 1 and they are being mutliplied

2. divide each term by x^degree (ind.variable)

3. substitution: v = y/x ←— always this

4. then solve like separable.

Reducible 2nd Order: Independent variable is visible

A(x)y’’ = y’ is an example

a substitution would be: y’ = v, y’’ = v’ —> v’ = dv/dx, v is a function of x

then separate so that v and x are isolated on different sides of the equation

integrate to solve for v and then put back in y for v and finish solving for y

Reducible 2nd Order: Independent variable is invisible

A(y)y’’ = y’

Idea: let y be our new independent variable y will play role of x.

dy/dx=y’=v, derivative, y’’ = dv/dx * dv.dy dy/dx = dv/dy v

use this as your substitution, and solve

Application of First Order : Mixing Problem

What would be given:

rin = rate of solution in

cin = concentration of salt in

vo = initial volume of water in

yo = initial amount of salt in

rout = rate of solution out

y(t) = amount of salt in tank at time t

goal: find y(t)

iDEA: rate of change of salt tank = rate of salt (in - out)

dy/dt = rin*cin - rout*cout

cout = y/vo +(rin-rout)t : amount of salt in / vol of water in tank

so put together:

dy/dt = rin*cin - rout * (y/ vo+(rin-rout)t)

Euler’s Method ( Method to approximate a solution)

Given: y’ = f(x,y) ; y(xo)=yo ; h = step size

asked to estimate/approximate y(x)

y_n+1 = y_n + h * f(x_n, y_n)

Autonomous Diff Equation

Form: dy/dt = f(y)

We can find what are call constant or equilibrium solutions, to find this do:

set f(y) =0 and solve for y

y = some constants, and those are called the critical points.

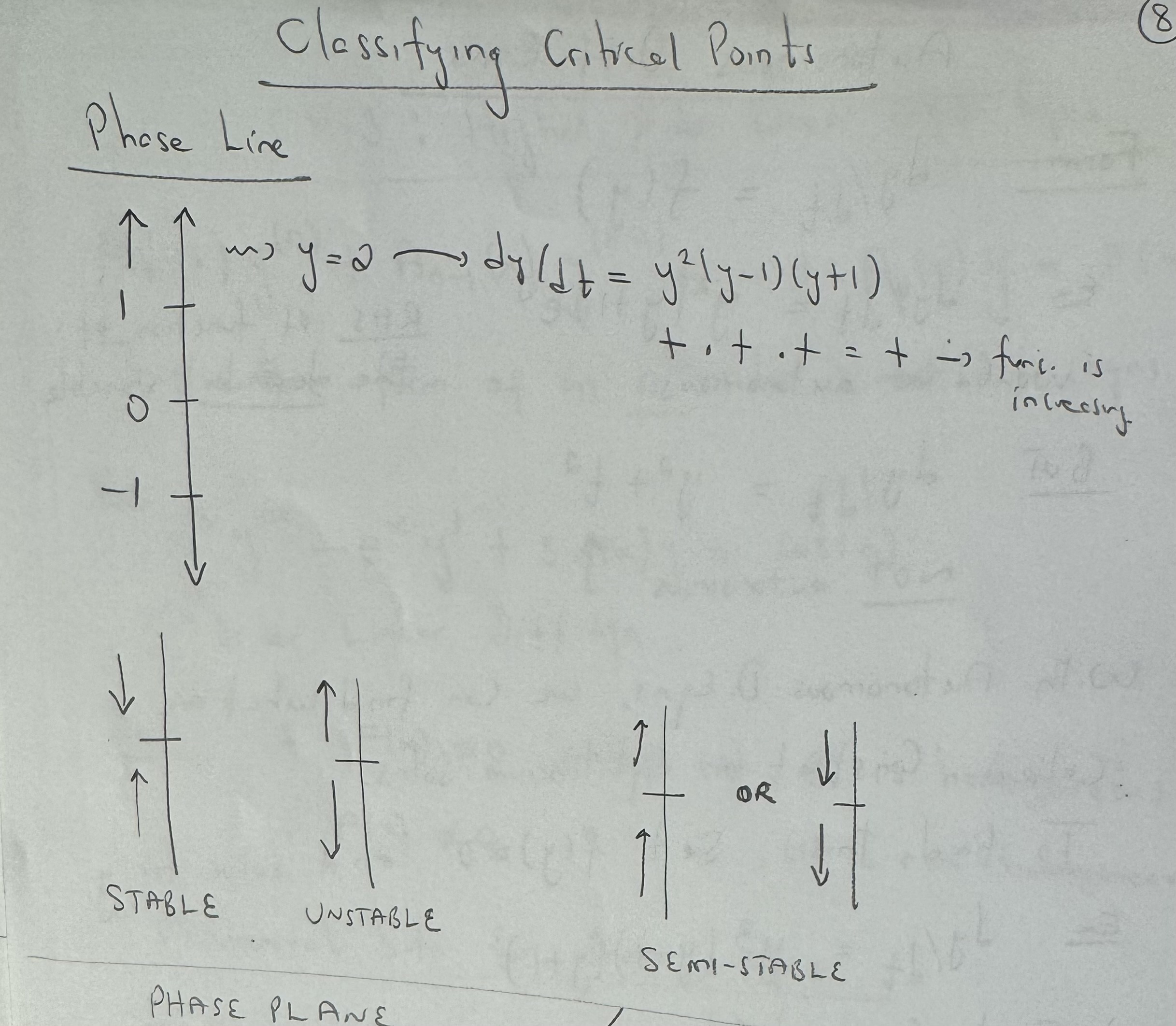
Classifying Autonomous critical points

draw a graph, have the critical points be horizontal lines on the graph, and then find the slope fields of values above and below this line to indicate whether or not the graph is pointing towards or away from the horizontal line, if above and below the line are both pointing towards it, then it is a stable critical point, if both are pointing away, than it is unstable, and if one is point towards and one away, than it is a semi stable critical point. 

determine the slope field by plugging in a value for y in the dy/dt equation and that positive or negative sign will dictate the direction.

Higher Order Linear diff equs

Form of an nth order linear diff equ:

A_n(x)y^n+A_n-1(x)*y^(n-1) + …+ A_o(x)y= F(x)

If F(x) = = 0 than the equation is homogeneous

if it is no equal to zero it is non-homogeneous

General solution for Higher Order Linear diff equs

Case 1: Distinct, real roots

First: ay’’+by’+cy=0, a,b,c are constants

1. ar² + br +c = 0 : characteristic equation, find the roots

2. r = j,k, whatever

3. y= C_1e^(r1x) + C_2e^(r2x)

General solution for Higher Order Linear diff equs

Case 2: Repeated real roots, r

First: ay’’+by’+cy=0, a,b,c are constants

1. ar² + br +c = 0 : characteristic equation, find the roots

2. r = +- k

3. y= C_1e^(rx) + C_2xe^(rx)

General solution for Higher Order Linear diff equs

Case 2: Complex roots r = a+- b i

First: ay’’+by’+cy=0, a,b,c are constants

1. ar² + br +c = 0 : characteristic equation, find the roots

2. prob use quadratic formula to find r and it will be

   1. r = w +- k i 

3. y = C_1e^(ax)*cos(kx) +C_2e^(ax)*sin(kx)