UPTP INGRESO 2023

Ley del Seno

proporción existente entre los lados y senos de los ángulos de un triángulo.

a/sen(a) = b/send(b) = c/sen(c)

Ley del coseno

el cuadrado de un lado es igual a la suma de los cuadrados de los lados restantes menos el cos del lado elegido por el producto de los lados restantes.

a²=c²+b²-2cos(a)×c×b

Seno de suma o resta de ángulos

sen(a+b) = sen(a)cos(b) + sen(b)cos(a)

Coseno de suma o resta de angulos

cos(a±b) = cos(a)cos(b) -/+ sen(b)sen(a)

Suma a multiplicacion de senos

sen(a) + sen(b) = 2sen((a+b)/2)cos((a-b)/2)

Resta a multiplicacion de Senos

sen(a) - sen(b) = 2sen((a-b)/2)cos((a+b)/2)

Suma a multiplicacion de cosenos

cos(a) + cos(b) = 2cos(a+b/2)cos(a-b/2)

Resta de cosenos a multiplicacion

cos(a) - cos(b) = -2sen(a+b/2)sen(a-b/2)

Multiplicacion a suma de seno por coseno

sen(a)cos(b) = ½(sen(a+b) + sen(a-b))

Multiplicación a suma de seno por seno

sen(a)sen(b) = ½(cos(a+b) - cos(a-b))

Multiplicación a suma de coseno por coseno

cos(a)cos(b) = ½(cos(a+b) + cos(a-b))

Summ of arithmetic sequence

S = n(a1 + an)/2

Summ of geometric sequence

S = a1(r^n - 1)/r-1

Heron's formula

√(s(s-a)(s-b)(s-c)) where s is the semi-perimeter of the triangle, and a, b and c being the corresponding sides.

sen(π/3)

√3/2

Send(π/6)

½

Sen(π/4)

√2/2

Sen(0)

0

Send(π/2)

1

Cos(π/3)

½

Cos(π/6)

√3/2

Cos(π/4)

√2/2

Cos(0)

1

Cos(π/2)

0

Tg(π/3)

√3

Tg(π/6)

√3/3

Tg(0)

0

Tg(π/2)

Indefinido.

Log(2)

0.301

Log(3)

0.477

√2

1,41

√3

1,73

√5

2,23

Limacons

a ± b(sen(a))

a ± b(cos(a))

Circles

r = a

r = asen(x)

r = acos(x)

Trigonometric equations

a(sen(k(x-h)) or cos

Where a is the amplitude, w is the speed, and h is the horizontal shift.

t = 2π/k (π/k for tg), where t is the period (f = 1/t)

Amplitude (shifted vertically)

(Max value + |min value|) /2

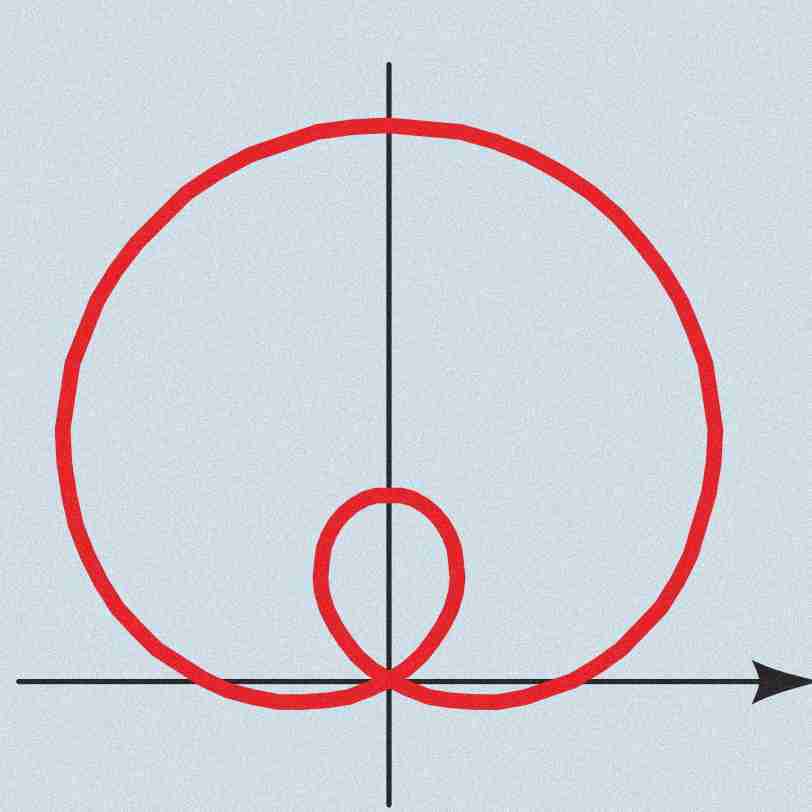
Limacon with inner loop

a ± bsen(x) where a < b

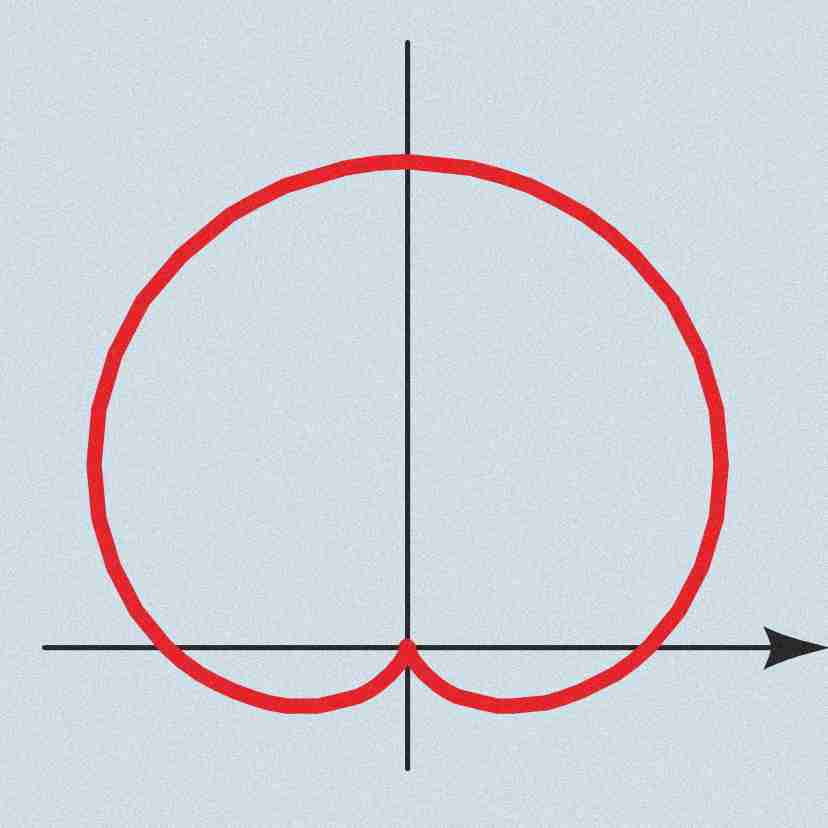
Cardiod

a ± bsen(x) where a = b

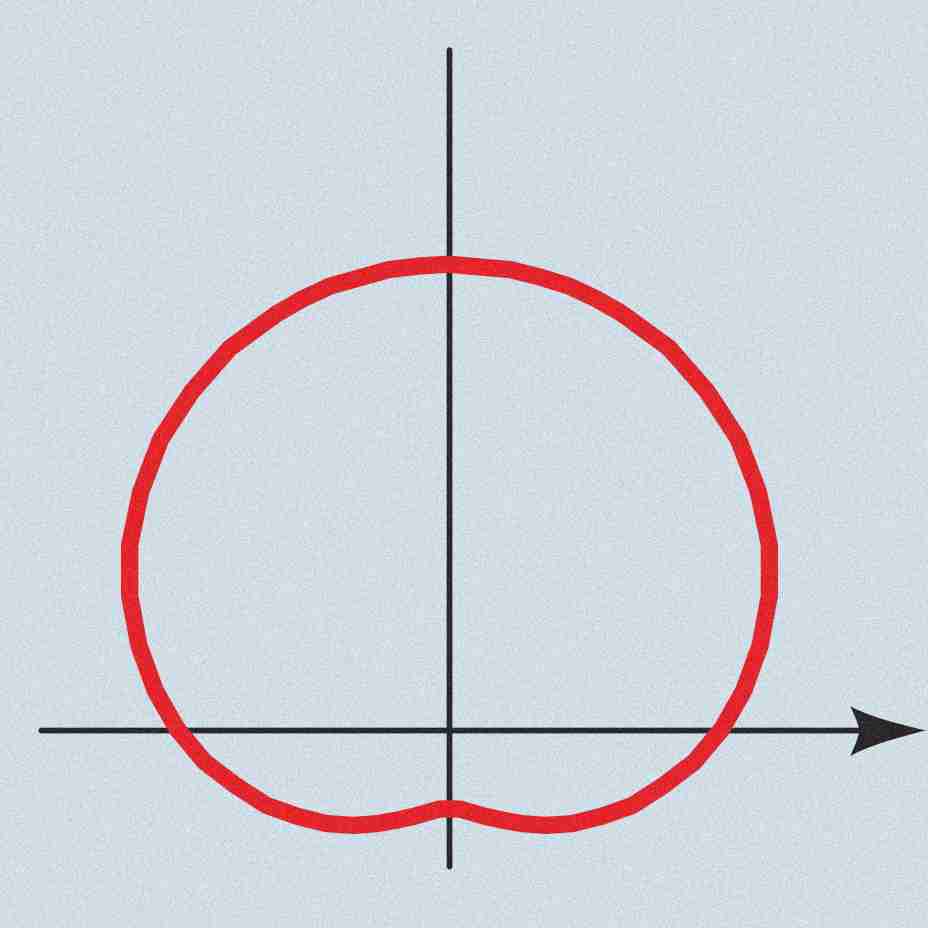
Dumped limacon

a ± bsen(x) where a > b

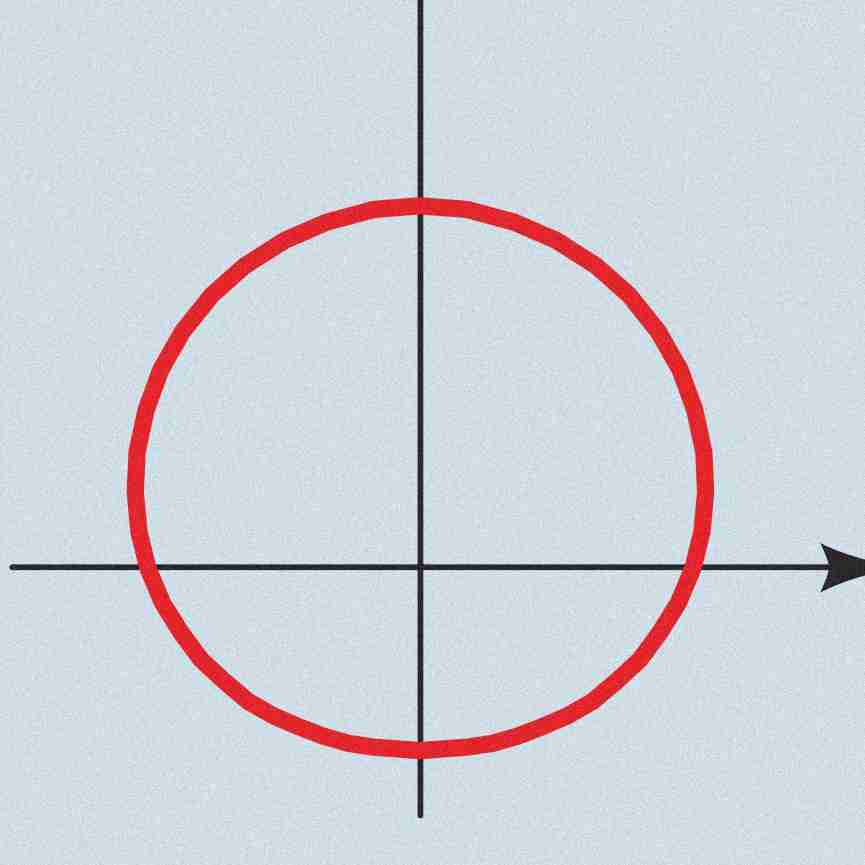
Convex limacon

a ± bsen(x) where a >= 2b

Spiral

r = aΩ

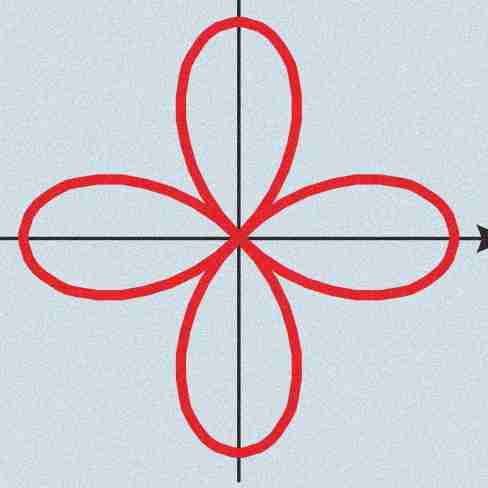
Rose with even amount of leaves

a(sen(nΩ)) where n is even and there's 2n petals

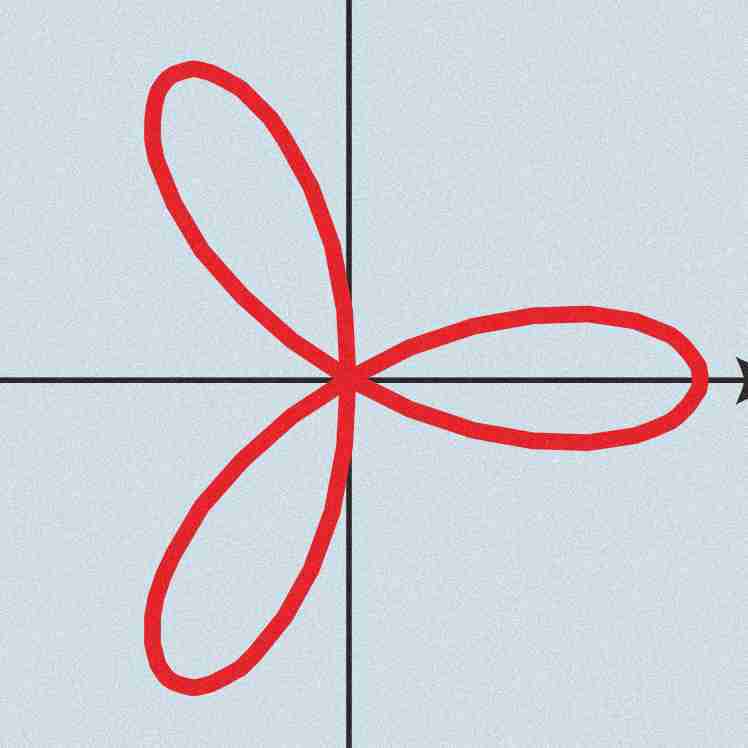
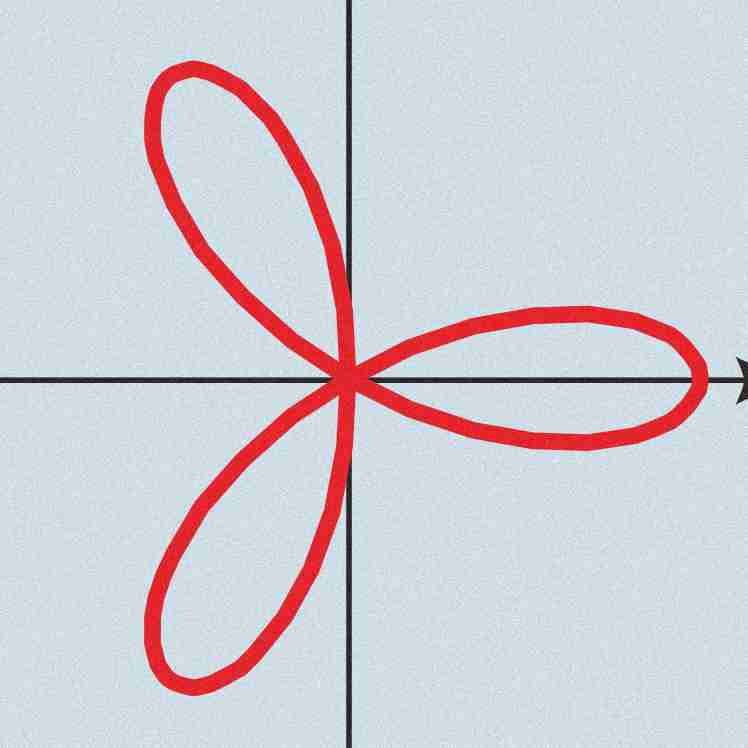
Rose with odd amount of petals

a(sen(nΩ)) where n is odd, and there's n petals

Dot product

a•b = |a||b|cos(θ)

Cross product

a×b = |a||b|sen(θ)

Moivre´s theorem

zⁿ = rⁿ (cos(rθ) + sin(rθ)i), where r is the module of z, and θ is the angle that z creates with x and y (tg^-1(y/x)

z₁/z₂

r1/r2(cos(θ1-θ2) + sen(θ1-θ2))

z₁*z₂

r₁*r₂(cos(θ₁+θ₂) + sen(θ₁+θ₂))

Projection of U onto V

(A•V/|V|²)* V

Sen(π+x)

-sen(x)

Sen(π/2 + x)

Cos(x)

Sen(π/2 - x)

Cos(x)

Cos(π+x)

-cos(x)

Tg(π+x)

Tg(x)

Cos(π/2 + x)

-sin(x)

Cos(π/2 - x)

Sin(x)

Tg(π/2+x)

-cotg(x)

Tg(π/2 - x)

Cotg(x)

Sin(-x)

-sin(x)

Cos(-x)

cos (x)

tg(-x)

-tg(x)

Suma o resta de ángulos en tangente

tg(a+b) = tga ± tgb / 1 ± tga*tgb

Medio ángulo de seno

√(1-cos/2)

Medio ángulo de coseno

√(1+cos/2)

Medio ángulo de tg

sin(x)/1+Cos(x) = 1-cos(x)/sin(x)

y > |x|

espacio chiquito

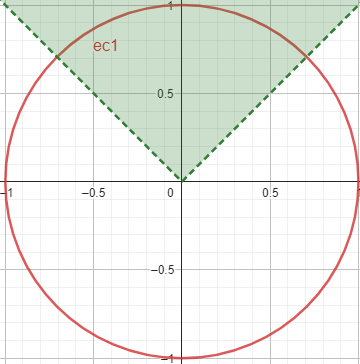
x > |y|

espacio chiquito

range of sin^-1

− π/2 to π/2

range of cos^-1

0 to π

range of tg^-1

− π/2 to π/2

Binomio cubo

(a±b)³ = a³±3a²b+3ab²±b³

Suma y resta de cubos

a³ ± b³= (a ± b)( a²-/+ ab + b² )

Infinite geometric progression formula

a₁/1-r

Compound interest

A = P(1+r/n)^nt where p is inital value, r is interest rate, n is amount of times per year and t is years

Pythagorean identities

Tg²(x)+ 1 = sec²

Cotg(x)² +1 = csc²(x)

sen²(x)+ cos²(x)= 1

Polar to linear

root(x + y) = r

r*cos(theta) = x

r*sin(theta) = y

y/x = theta

Discriminant of conics

Ax + Bxy + Cy + Dx + Ey + F

if B²- 4AC = 0 Is an parabola

if B² - 4AC > 0 Hyperbola

If B² - 4AC < 0 Elipse or circle

Newtons Cooling law

T_f = T_s + (T₀ - T_s) e^-r/t where T_s is the surrounding temperature, T₀ is the initial temperature and -r is the rate of change for the specific material.