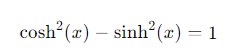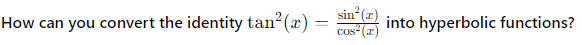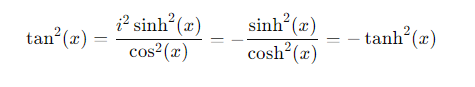Complex numbers

Year 1 semester 1

What is the standard form of a complex number?

Z=x+iy

x= real part

y= imaginary part

When are 2 complex numbers (Z₁=x₁+iy₁, Z₂=x₂+iy₂) equal?

If their real and imaginary parts are equal

x1=x2

y1=y2

If you let Z₁=x₁+iy₁ and Z₂= x₂+iy₂, how do you add them together (Z₁+Z₂)?

Z₁+Z₂= (x₁+x₂)+i(y₁+y₂)

If you let Z₁=x₁+iy₁ and Z₂= x₂+iy₂, how do you subtract them (Z₁-Z₂)?

Z₁-Z₂= (x₁-x₂)+i(y₁-y₂)

If you let Z₁=x₁+iy₁, how would you go about the negation of Z₁?

-Z₁=-x₁+i(-y₁)—> -x₁-iy₁

If you let Z₁=x1+iy₁ and Z₂= x₂+iy₂, how do you multiply them?

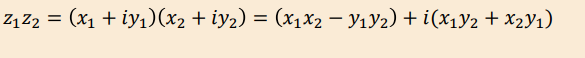
What does commutativity mean with complex numbers?

It means Z₁ x Z₂=Z₂ x Z₁

What does associativity mean with complex numbers?

(Z₁ x Z₂)Z₃= Z₁(Z₂ x Z₃)

If 𝑧 = 𝑥 + 𝑖y, what is the formula for the inverse of z (1/z)?

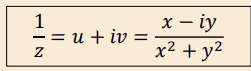
What is the symbol for a complex conjugate?

Z*

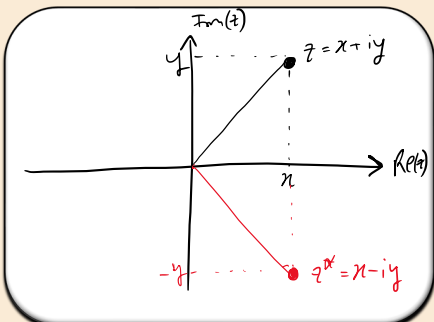
How do you find the complex conjugate of a complex number?

Replace i with -i

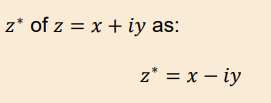
What happens when you multiply a complex number with its complex conjugate?

It always gives a real, positive number

If Z=x+iy

Z*=x-iy

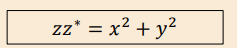
What do you get if you do (Z*)* ?

(Z*)*= Z

What do you get if you do Z+Z* ?

If Z=x+iy

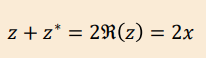
What do you get if you do Z-Z* ?

If Z=x+iy

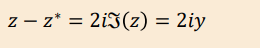
How do you divide complex numbers (Z1/Z2)?

1) Express the division as a fraction

2) Multiply the top and bottom by the complex conjugate of the denominator

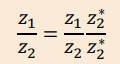
What are the two square roots of i?

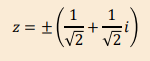
What is the graphical representation of complex numbers called?

The Argand Diagram.

What is the modulus of a complex number z=x+iyz

The modulus ∣z∣ is the distance from z to the origin in the Argand Diagram.

How is the modulus of z=x+iyz calculated?

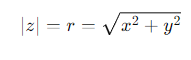
What is ∣z∣² in terms of x and y?

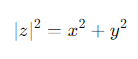
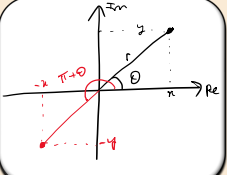
What is the argument of a complex number z?

The argument arg(z) is the angle θ between the positive x-axis and the line joining z to the origin.

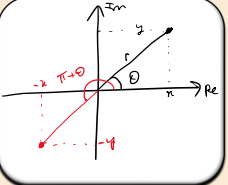
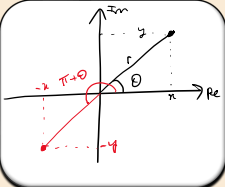
How is arg(z) calculated for z=x+iy?

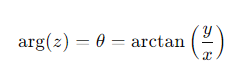
In which direction is the argument measured as positive?

The anticlockwise direction is positive by convention.

What adjustment might be necessary when calculating arg(z)?

If z is in the second or third quadrant, add π or subtract π to the result to get the correct angle.

What is the principal value of arg(z)?

The principal value lies in the range:

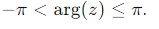
Can a complex number z have multiple values of arg(z)?

Yes, the argument can differ by multiples of 2π:

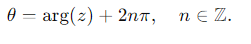
What are the two main ways to represent a complex number z on the Argand Diagram?

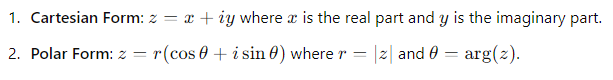
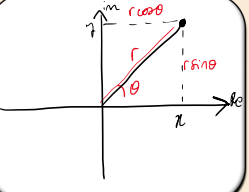
What do r and θ represent in polar coordinates?

• r=∣z∣ is the modulus (distance from the origin).

• θ=arg(z) is the argument (angle from the positive x-axis).

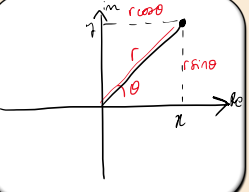
How do you convert from Cartesian to Polar form?

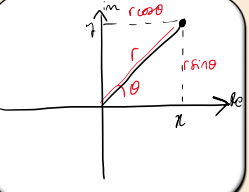
How do you convert from Polar to Cartesian form?

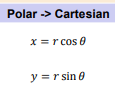
What is the polar form of z=x+iy?

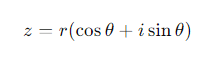
What is Euler’s equation?

It connects exponential and trigonometric functions through complex numbers

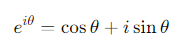
How can we represent a complex number z=x+iy in exponential form?

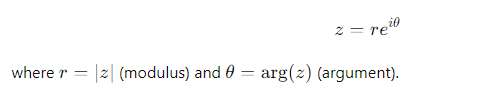
What are the three main forms of a complex number?

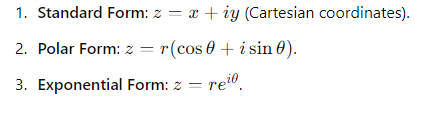
What are the modulus and argument of z=re^iθ?

• Modulus: ∣z∣=r

• Argument: arg(z)=θ

How are the polar form and exponential form of a complex number related?

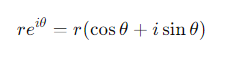
How do you represent the inverse of a complex number z in exponential form?

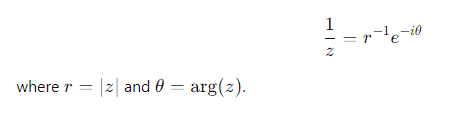
How do you multiply two complex numbers in exponential form?

• Modulus: ∣z₁z₂∣=r₁r₂

• Argument: arg(z₁z₂)=θ₁+θ₂

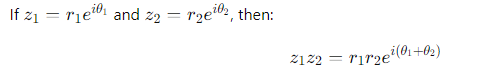
How do you divide two complex numbers in exponential form?

• Modulus: ∣z₁/z₂∣=r₁/r₂

• Argument: arg(z₁/z₂)=θ₁−θ₂

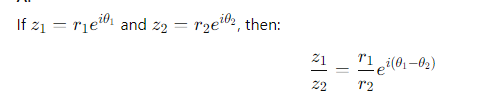
What is the general form for the square root of a complex number in exponential form?

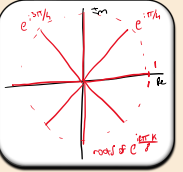
What is the general formula for the nth roots of unity?

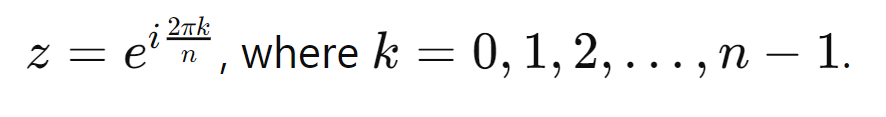
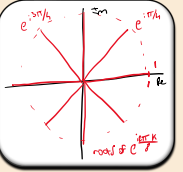
What are the nth roots of unity in exponential form?

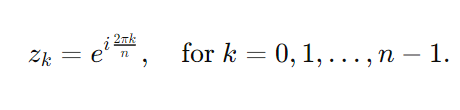
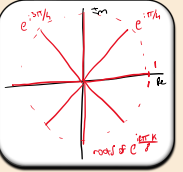
How do you compute the angle between consecutive nth roots of unity?

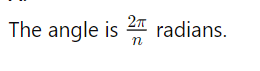
Where do the nth roots of unity lie on the Argand diagram?

All roots lie on the unit circle, equally spaced at angles of 2π/n radians apart.

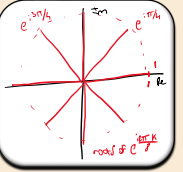
What equation defines the natural logarithm of a complex number z?

The natural logarithm w=ln⁡z satisfies z=e^w

What is the general form of the natural logarithm of a complex number?

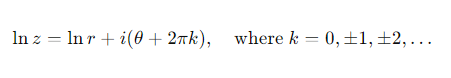
How do the modulus and argument of z relate to ln⁡z?

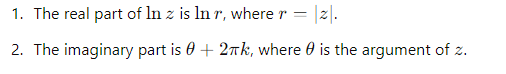
What is the principal value of the complex logarithm?

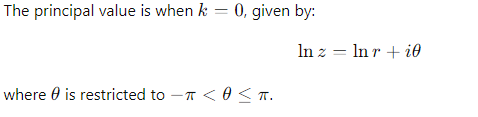
How do you compute ln⁡z if z=x+iy?

How do we deal with powers where the exponent is a complex number, such as a^z?

What is the general form for complex powers?

For a^z, where a is a positive real number and z is a complex number:

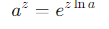
What is De Moivre's Theorem?

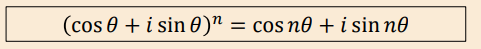
What is Euler’s equation?

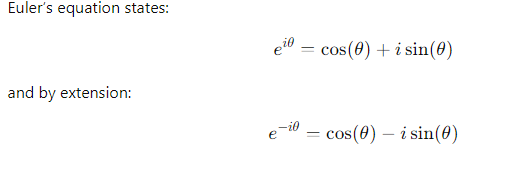
How do you define the hyperbolic tangent tanh⁡(θ)?

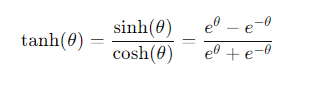
Hyperbolic functions graphs

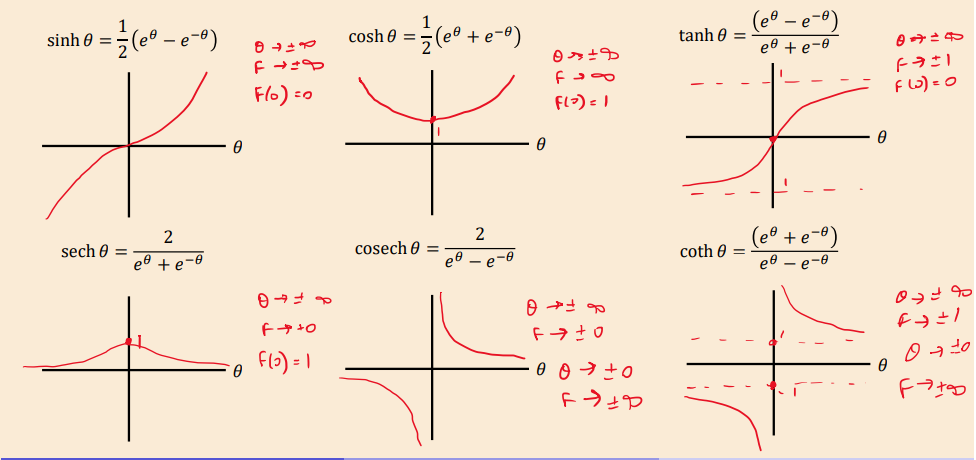
How do you translate cos⁡(x) and sin⁡(x) into hyperbolic functions?

How do you translate cosh⁡(x) and sinh⁡(x) back into trigonometric functions?

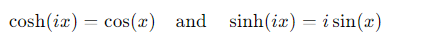
What happens to the identity cos⁡²(x)+sin⁡²(x)=1 when translated into hyperbolic functions?