2.3 PROPORTIONAL REASOINING

2.3 PROPORTIONAL REASOINING

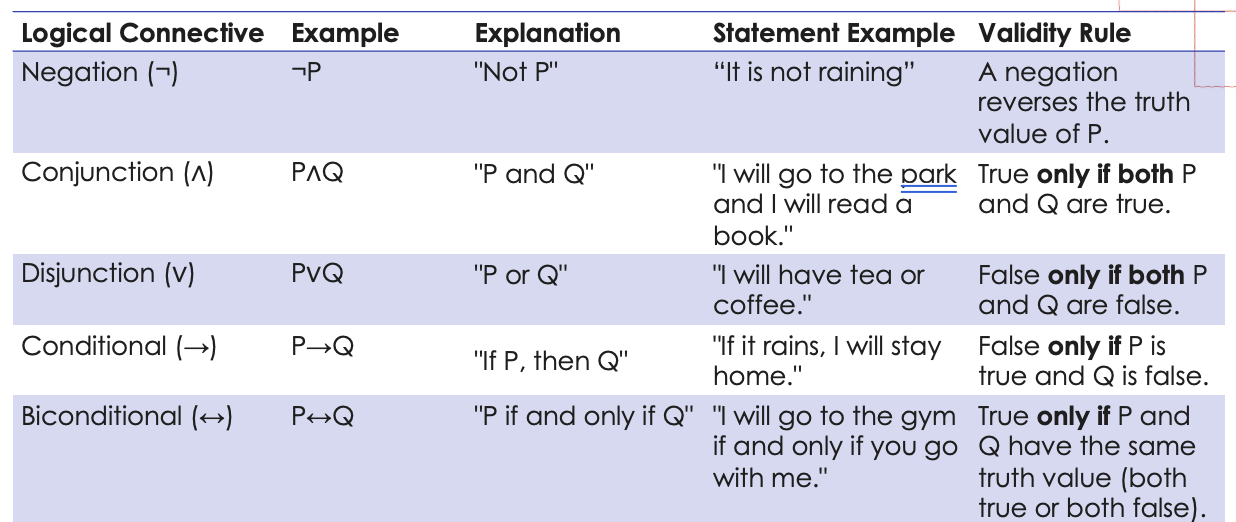
Connectors

• Negation “not”

• Conjunction "and"

• Disjunction "or one thing, or another, or both"

• Disjunction "or one thing, or another, but not both"

• Conditional "If p then q"

• Biconditional "If and only if p then q"

Differences between types of deductive reasoning

• Syllogistic Reasoning

• Propositional Reasoning

Syllogistic Reasoning found in two types →

• Transitive or Linear Reasoning

• Categorical Reasoning

Transitive or Linear Reasoning

• propositions with internal relations like "more than/ less than”

• example → Louis is older than Charlie, Charlie is older than Joan, therefore Louis is older than Joan.

Categorical Reasoning

• involves propositions with quantifiers such as "all," "some," or "none."

• example → All men are mortal, Socrates is a man, therefore Socrates is mortal.

Propositional Reasoning

• establishing relationships between propositions using connectors like the conditional (if p → q), disjunction (either one or the other), or conjunction (both).

• Example → Today I will study (p) and go for a walk (q)" (conjunction), when can it be said that the statement is true? The proposition is true when both "Today I will study" and "I will go for a walk" are true.

Formal or propositional logic

• analyses the relationships between propositions in a statement with the goal of constructing valid arguments that satisfy the basic principle of deductive reasoning.

This principle states (propositional reasoning)

• if all the premises are true, there is no possibility that the conclusion is false; in other words, the conclusion must also be true.

Example of Valid Propositional Reasoning

•Premise 1: "If it rains, the street gets wet."

•Premise 2: "It has rained.“

What can be inferred/concluded/deduced?

•The street is wet. 

(relevant to modus ponens & modus tollens)

Example of Invalid Propositional Reasoning

•Premise 1: "If it rains, the street gets wet."

•Premise 2: "The street has gotten wet.“

What can be inferred/concluded/deduced?

• Inferring that the street is wet because it has rained is an incorrect inference; it is not a logical consequence of the premises. The street may be wet for another reason, such as a passing water truck.

What is a Proposition

• smallest unit of speech

• can be true or false

Proposition Example

Today it will rain." This statement can be evaluated as either true or false.

Non-Proposition Example

• "Car." This is not a proposition because it doesn't make sense to ask if it is true or false.

Propositions are often represented by letters:

•Proposition 1: "Joan runs down the street" (p)

•Proposition 2: "Mary studies Chemistry" (q)

•Additional propositions can be represented by R, S, T, etc.(alphabetic after p & q)

Long sequence of statements contain:

• one or more propositions

• Propositions are connected through

• through connectors or connectives such as "and," "or," and "if...then..."

statement contains

• many propositions as there are parts subject to a truth value.

• The connectors link the propositions, establishing the type of relationship between them.

Example of a statement:

The other day I was walking down the street, and a dog jumped at me and bit me on the arm.“

• P: The other day I was walking down the street.

• Q: A dog jumped at me.

• R: It bit me on the arm.

Truth tables

• determine when a statement is true from given premises

• representation that includes all possible combinations of truth values for the propositions involved

In a truth table, we always have two possible values

• true & false → depends on propositions in the statement.

• represented as 2n → n is the number of propositions

Statement with one proposition

2 possible values (true, false

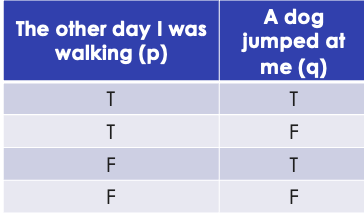
Statement with two propositions

• 4 possible values

• p = T, T, F, F,

• q = T, F, T, F

• 

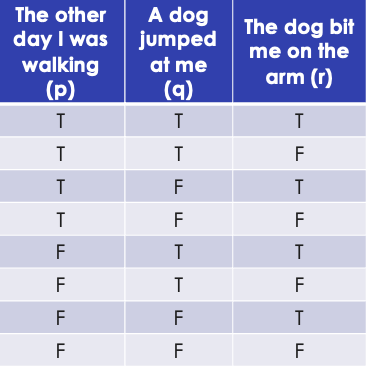
Statement with three propositions

• 8 possible values

• (p, q, r)

• 

Statement with four propositions

• 16 possible values

• (p, q, r, s)

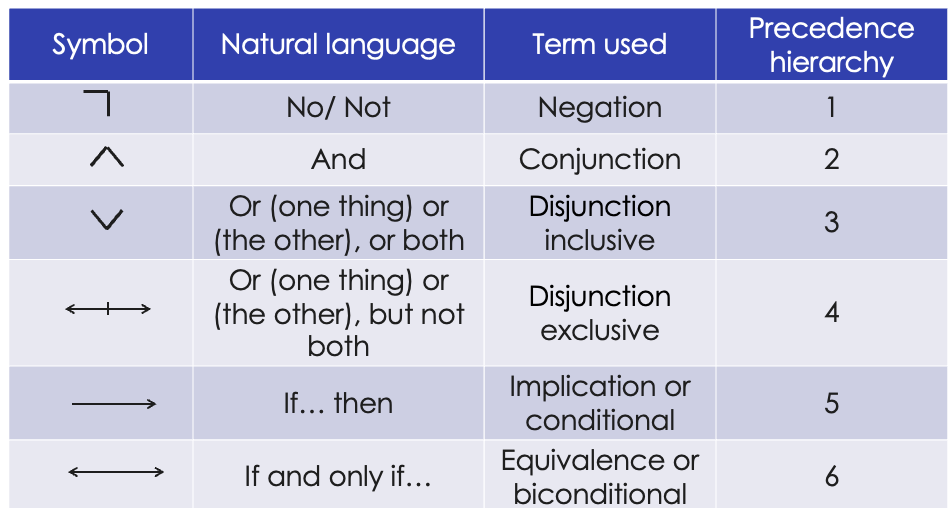
Connectors (or connectives)

• links that modify the truth value of propositions

• Each connector defines a specific "truth relation/table”

• can be single proposition or two propositions

•Connectors that apply to a single proposition

• •Negation: "not“

• ¬

Connectors that apply to two propositions

•Conjunction: "and" ^

•Disjunction: "or" (Note: There is no unequivocal linguistic translation, and its formulation can be ambiguous in various cases. There are two types of disjunction: inclusive and exclusive.)  ⅴ

•Implication: Conditional, "if ... then" →

•Equivalence: Biconditional, "if and only if ... then" (←>) 

Symbolic representation of connectors (or connectives)

Negation

• connector that transforms true into false & false into true.

  

Example of negation

Conjunction “and”

• connector that assigns a value of true to a statement only if both conditions are met. In all other situations, the value is considered false.

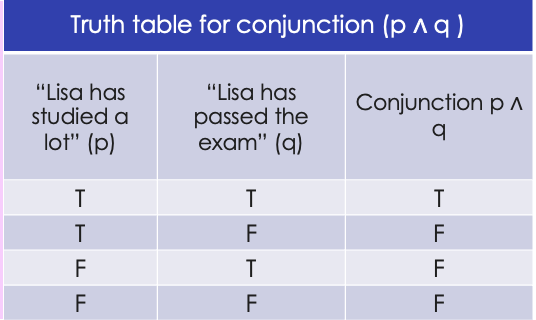
example of conjunction “and” /”but”

Example of a sentence with conjunction: Lisa has studied a lot (p) and has passed the exam (q).

When can we say that this statement is true?

Only in the case where Lisa has indeed studied a lot (true p) and has also passed the exam (true q). In all other cases, the statement will be false.

• If Lisa has studied a lot (true p), but ultimately fails (false q). à Then the statement “Lisa has studied a lot and has passed the exam" is false.

• If Lisa has not studied much (false p), but ultimately passes (true q). à Then the statement “Lisa has studied a lot and has passed the exam” is false.

• If Lisa has neither studied much (false p) nor passed (false q). à Then the statement “Lisa has studied a lot and has passed the exam” is false.

Inclusive disjunction

“or one thing, or another, or both”

• connector that makes the statement always true unless both propositions are false.

• It produces a true value if at least one of the two statements is true, and false if both statements are false.

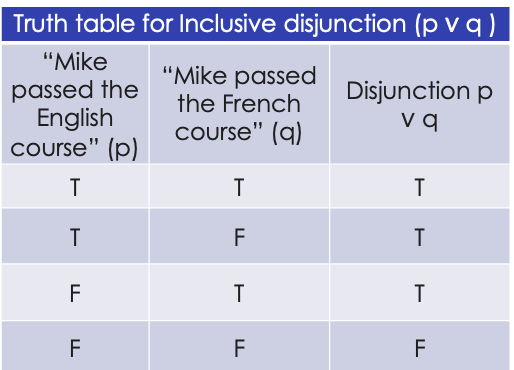
example of inclusive disjunction

Exclusive disjunction

• “or one thing, or another, but not both”

• connector that makes the statement true, as long as one of the propositions is true and the other is false.

• 

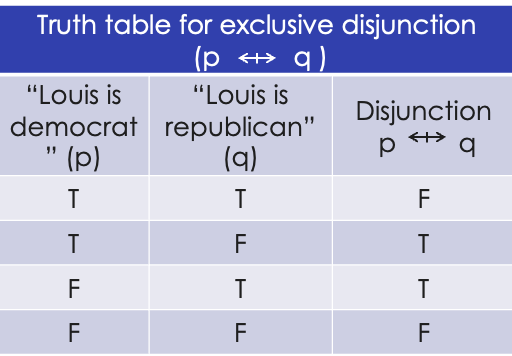
example of exclusive disjunction

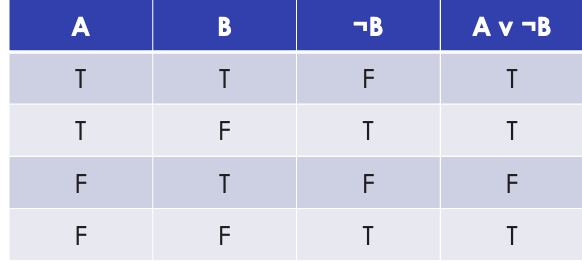
truth table of A v ¬B

conditional connectors

• “if p then q”

  

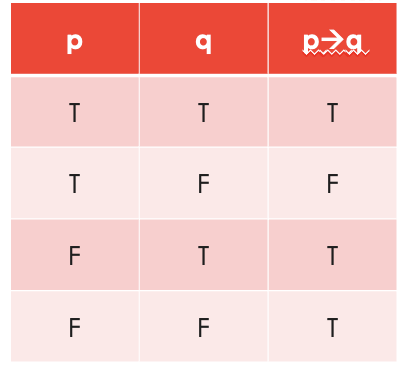
example of conditional connectors

creation of (P ∧ ¬Q) truth table 

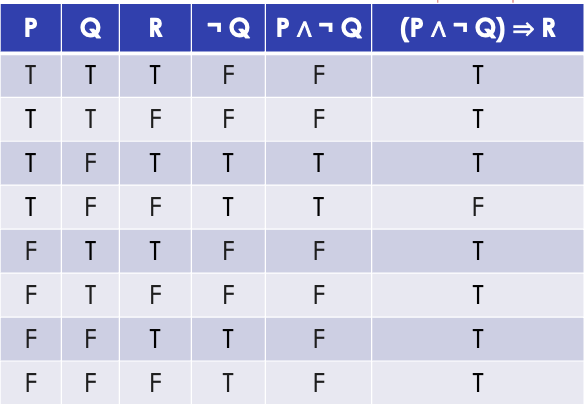
Biconditional

• “if and only if p then q”

• connector that makes the statement true as long as both the antecedent (p) and the consequent (q) are either both true or both false.

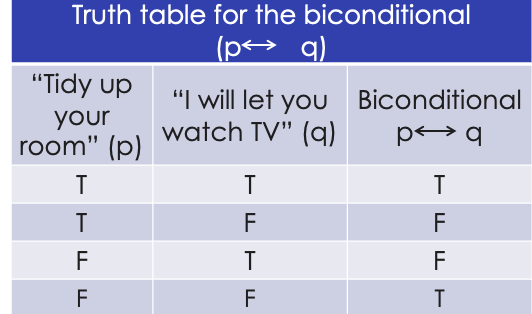
example of bidirectional

Connectors or connectives. Summary

Propositional reasoning establishes

• relationships between propositions using connectors such as the conditional (if p → q), disjunction (either one thing or another), or conjunction (both one thing and another). 

Formal logic determines

• when we have correctly applied the rules underlying deductive reasoning. 

Formal or propositional logic

• analyses the relationships between propositions in a statement

• the purpose of constructing valid arguments that satisfy the basic principle of deductive reasoning

• “If all the premises are true, there is no possibility that the conclusion is false (therefore the conclusion must also be true).” 

To determine when a statement is true happens when

• when we can reach a conclusion from given premises, truth tables are used. 

The relationships between propositions involved in a statement are

• modified by connectors, each of which defines a specific "truth relation" (truth table) for the statements to which these connectors apply.