BMF additional questions

Mock 2, 3, 4, 8, 9, 10, 11, 12

In which of the following scenarios would a chargeable gain or capital loss be realised?

a) Suki gives £10,000 cash to her niece.

b) James gives his niece a small plot of land.

c) Suren’s car is sold to a neighbour.

d) Ahmed’s grandfather was awarded a medal for bravery during the Second World War. He left it to Ahmed in his will. Ahmed has decided to sell the medal to an antiques dealer.

9.1

The correct answer is b.

Each of the individuals is a chargeable person. Each sale or gift is a chargeable disposal. The passing of the medal to Ahmed from his grandfather was on his death so there is no chargeable gain or capital loss as a result of the inheritance.

The final thing to establish is whether any of the assets are exempt assets. If they are not, a chargeable gain or capital loss will arise. Sterling currency (cash), the car and the medal awarded for valour (as opposed to being purchased) are all exempt assets. The small plot of land is not and is therefore a chargeable asset. 

The necessary three elements, chargeable person, chargeable disposal and chargeable asset are only present in answer b.

Priyanka acquired a small allotment a few years ago that she used to grow her own vegetables. She paid £82,500 at that time and after 18 months built a small shed which cost £500 to store her gardening tools on the allotment rather than bring them from home every time. She has sold it for £117,850 during the tax year. She has legal fees in connection with the sale of £2,400 and paid a valuer £1,200 to value the allotment before she sold it. 

The calculation of the chargeable gain or capital loss for this disposal is as follows:

9.1

	£	£
Disposal value (gross sale proceeds)		117,850
Less incidental costs of disposal (£2,400 + £1,200)		(3,600)
Net sale proceeds		114,250
Less Cost
Acquisition cost	(82,500)
Enhancement expenditure	(500)
		(83,000)
Chargeable gain		31,250

Adam disposes of two assets during the tax year. On 14 September, he gives his friend Arabella a valuable vase worth £25,600. Adam had bought the vase in June 1990 for £7,500 and had paid commission of £750 on the purchase.

On 3 December, Adam sells a painting for £76,400 and incurs selling fees of £1,000. 

Adam inherited the painting in July 1986 when it was worth £14,740.

Calculate the chargeable gains on the assets.

Chargeable gain on sale of painting:

9.1

The answer is £60,660.

The painting was received via an inheritance and therefore the market value at the time it was inherited (probate value) will be the deemed acquisition cost for Adam.

	Painting
	£
Disposal value (market value / gross proceeds)	76,400
Less incidental costs of disposal	(1,000)
Net sale proceeds	75,400
Less acquisition cost / probate value	(14,740)
Less cost of acquisition	(0)
Chargeable gains	60,660

Priyanka, from the previous example, inherited a sizeable collection of valuable early 20th century stamps from her aunt when it was worth £22,300. Priyanka is not really interested in collecting stamps and has decided to renovate her house. To help fund the renovation she has decided to sell the stamp collection to a dealer for £15,460.

The calculation of the chargeable gain or capital loss for this disposal is as follows:

9.1

	£
Disposal value (gross sale proceeds)	15,460
Less incidental costs of disposal	(0)
Net sale proceeds	15,460
Less acquisition cost (probate value)	(22,300)
Less incidental costs of acquisition	(0)
Enhancement expenditure	(0)
Capital loss	(6,840)

Priyanka has a chargeable gain of £31,250 on the sale of her allotment and a capital loss on the sale of her stamp collection of £6,840 in the same tax year. Under step 2 of the process we looked at earlier, the capital loss on the disposal of the stamp collection is deducted from the chargeable gain on the disposal of the allotment. calculate the net chargeable gain for the tax year? and Priyanka’s AEA would be applied?

9.1

	£
Chargeable gain for the tax year	31,250
Deduct capital loss for the tax year	(6,840)
Net chargeable gain for the tax year	24,410
Deduct annual exempt amount	(3,000)
Taxable gain for the tax year	21,410

Adam who we met earlier and who had disposed of a vase and a painting during the year. 

We saw that he had made chargeable gains on these disposals of £17,350 and £60,660. 

Calculate Adam's taxable gains for the tax year, ie after deducting his annual exempt amount. 

9.1

Adam’s annual exempt amount of £3,000 would be deducted from the net chargeable gains for the tax year, of £78,010. This would leave £75,010 subject to CGT. 

	£
Chargeable gains for the tax year	78,010
Deduct capital losses for the  tax year	-
Net chargeable gains for the tax year	78,010
Deduct annual exempt amount	(3,000)
Taxable gains for the tax year	75,010

Imogen (a higher rate taxpayer) bought an asset for £5,000 and later sells it to her sister Jessica. At the date of sale, the asset is worth £19,000 but Imogen sells it to Jessica for £8,000.

Why did Jessica sell the asset for £8,000?

9.1

By selling the asset for £8,000 Imogen would calculate a gain of £3,000 (proceeds £8,000 less cost £5,000). This would be covered by her AEA and would therefore not be subject to tax. Perhaps Jessica would give Imogen the other £11,000 at a later date and, as cash is an exempt asset, this would not be subject to CGT.

However, because of the non-arm’s length / connected persons rules, Imogen must calculate her chargeable gain using the market value of £19,000 as the disposal value. The chargeable gain would therefore be £14,000.

Cordelia sells a painting for £45,000, realising a chargeable gain of £2,500 in the 2024/25 tax year. how much does she need to report the chargeable gain?

9.1

Cordelia has proceeds below £50,000 and a chargeable gain below the AEA so does not need to report the chargeable gain.

Hamish makes chargeable gains of £14,500 on a gift of shares worth £35,000 in the 2024/25 tax year. Hamish also has a capital loss of £12,000 in 2024/25. There are no capital losses brought forward.

Calculate taxable gains for the tax year

9.1

	£
Chargeable gains for the tax year	14,500
Deduct capital losses for the tax year	(12,000)
Net chargeable gains for the tax year	2,500
Deduct annual exempt amount	(2,500)
Taxable gains for the year	0

Despite having no CGT to pay for 2024/25 and having deemed proceeds (MV) of less than £50,000, Hamish must still report the chargeable gain, as the amount before deducting capital losses is greater than the AEA for the year.

A part of Hamish’s AEA for 2024/25 is wasted.

Charles sells an antique sculpture for £23,000. The gain is £2,000. This is his only disposal in the tax year.

In the same tax year, Julie sells some shares for £23,000. The gain is £3,500. Julie also has a loss of £2,000 brought forward which was reported in an earlier tax year. 

Which taxpayer(s) will be required to report the chargeable gains arising in the 2024/25 tax year?

a) Neither Charles nor Julie will be required to report the chargeable gains

b) Only Charles will be required to report the chargeable gains

c) Only Julie will be required to report the chargeable gains

d) Both Charles and Julie will be required to report the chargeable gains

9.1

The correct answer is c

	Charles	Julie
	£	£
Net chargeable gains for the year	2,000	3,500
Deduct annual exempt amount	(2,000)	(3,000)
	0	(500)
Deduct capital losses carried forward from earlier tax years	-	(500)
Taxable gains for the tax year	0	0

Neither Charles nor Julie has total proceeds exceeding £50,000 nor do they have any CGT to pay as the net chargeable gains are covered by the annual exempt amount and capital losses. However, Julie will have to report her gains as they exceed £3,000 before deducting capital losses. She will have a capital loss of £1,500 remaining to carry forward.

Adam had taxable gains of £75,010 for the tax year after deducting the annual exempt amount.

To work out the CGT, we would need to know how much, if any, of his basic rate band for income tax has been used up in the tax year.

Assume that Adam had taxable income after the personal allowance from employment and savings of £27,700 in total for the tax year.

Calculate Adam’s CGT liability for the 2024/25 tax year.

9.2

The correct answer is c.

Adam has £10,000 of his basic rate band remaining (being the £37,700 basic rate band less the £27,700 taxable income).

So, £10,000 of his taxable gains would be taxed at 10% and the remaining £65,010 (being £75,010 less £10,000) taxed at the 20%. This is £14,002.00 as calculated below.

	£
£10,000 @ 10 %	1,000.00
£65,010 @ 20%	13,002.00
Total CGT due	14,002.00

Hugo is employed as a police officer and earns a salary of £32,270. He also has some property income of £4,700 in 2024/25. During the tax year he sells a few valuable antiques and makes chargeable gains totalling £24,250.

Calculate Hugo’s capital gains tax for 2024/25 and state the payment date

9.2

Income tax situation:	£
Net income (£32,270 + £4,700)	36,970
Personal allowance	(12,570)
Taxable income	24,400
Amount remaining in basic rate band (of £37,700)	£13,300
Chargeable gains situation:	£
Net chargeable gains	24,250
Deduct annual exempt amount	(3,000)
Taxable gains	21,250
These will be taxed as follows:
£13,300         @ 10%	1,330.00
£   7,950        @ 20%	1,590.00
Total capital gains tax	2,920.00
Due date	31 January 2026

Vlad has made chargeable gains and capital losses in the 2024/25 tax year as follows:

	£
Flat in Edinburgh used as a holiday home	42,000
Sale of an antique vase	(7,400)
Sale of shares	25,500

The sale of the flat is a disposal of residential property, and the chargeable gain is subject to CGT rates of 18% and 24%. It is most beneficial to deduct capital losses and the AEA from this gain as far as possible first.

Vlad has taxable income (after the personal allowance) of £45,700 and has capital losses carried forward from earlier tax years of £17,000.

Vlad has taxable income above his basic rate limit.

The calculate the most beneficial way of the CGT (Capital Gains Tax) due from Vlad

9.2

The most beneficial way to calculate the CGT due from Vlad, as a result of the higher rates of CGT charged on taxable gains on residential property, is to deduct capital losses and the AEA from the chargeable gain on the residential property first as far as possible.

	Residential property	Other gains	Total
	£	£	£
Edinburgh flat	42,000	-	42,000
Shares	-	25,500	25,500
Antique vase	(7,400)	-	(7,400)
Net chargeable gains for the year	34,600	25,500	60,100
Deduct annual exempt amount	(3,000)	-	(3,000)
	31,600	25,500	57,100
Deduct capital losses carried forward from earlier tax years	(17,000)	-	(17,000)
Taxable gains for the year	14,600	25,500	40,100
	£	£	£
£25,500 @ 20%	-	5,100.00	5,100.00
£14,600 @ 24%	3,504.00	-	3,504.00
CGT liability	3,504.00	5,100.00	8,604.00

This way of deducting the capital losses and AEA reduces the taxable gains subject to the higher residential property rates of CGT as far as possible, leaving more taxable gains subject to the standard rates.

Delilah earns £57,420 in the tax year from her employment. She also receives £2,500 of rental income from letting out her holiday home when she is not using it herself.

Delilah sells her holiday home realising a gain of £48,100. In the same year she also realises gains of £10,000 on the sale of some shares and £3,000 on the sale of a plot of land. She has a capital loss carried forward from earlier tax years, of £12,000.

Calculate Delilah’s capital gains tax liability for the tax year

9.2

With taxable income of £47,350 (£57,420 + £2,500 - £12,570), Delilah has none of her basic rate band remaining. To minimise her CGT liability, it would be beneficial to deduct the AEA and capital losses from the gain on the residential property, as this gain is subject to higher rates of tax than the other gains. 

	Residential property gains	Other gains	Total
	£	£	£
Holiday home	48,100	-	48,100
Shares	-	10,000	10,000
Land	-	3,000	3,000
Net chargeable gains for the tax year	48,100	13,000	61,100
Deduct annual exempt amount	(3,000)	-	(3,000)
	45,100	13,000	58,100
Deduct capital losses brought forward	(12,000)	-	(12,000)
Taxable gains	33,100	13,000	46,100
	£	£	£
£33,100 @ 24%	7,944.00	-	3,570.00
£13,000 @ 20%	-	2,600.00	2,600.00
Tax payable	7,944.00	2,600.00	9,833.00

A few years ago, Chloe gave her husband, Louis, a valuable vase worth £20,000. Chloe had bought the vase in January 1997 for £12,000. Louis sells the vase in January of this year for £22,000.

Calculate the chargeable gain when Chloe gave the vase to Louis and also when Louis sold the vase this year.

9.3

	Chloe to Louis £	Sale by Louis £
Disposal value (original cost / actual proceeds)	12,000	22,000
Acquisition cost	(12,000)	(12,000)
Chargeable gain	0	10,000

A few years ago, Chloe gave Louis, a valuable vase worth £20,000. Chloe had bought the vase in January 1997 for £12,000. Louis sells the vase in January of this year for £22,000. Louis and Chloe live together but are not married (ie are common law spouses).

Calculate the chargeable gain when Chloe gave the vase to Louis and also when Louis sold the vase this year.

9.3

The no gain / no loss rule only applies to spouses. If Louis and Chloe are not married or in a civil partnership, the non-arm’s length rule would apply as follows:

	Chloe to Louis £	Sale by Louis £
Disposal value (MV/actual proceeds)	20,000	22,000
Acquisition cost	(12,000)	(20,000)
Chargeable gain	8,000	2,000

Si bought a plot of land for £17,000 and incurred purchase fees of £1,000. Si disposed of one-quarter of the field for proceeds of £30,000 and incurred expenses on disposal of £1,200. The remaining three-quarters of the plot of land was valued at £31,500.

Calculate the chargeable gain on the disposal.

9.3

	£
Disposal value (gross sale proceeds)	30,000
Incidental costs of disposal	(1,200)
Net sale proceeds	28,800
Acquisition cost. Working. A / A+B x £ Original cost: £30,000 / (£30,000 + £31,500) x (£17,000 + £1,000)	(8,780)
Chargeable gain	20,020

Note that the total cost of £17,000 plus costs of £1,000 is apportioned. The apportionment is always calculated using the formula and never based on the proportion of the part of the asset disposed of (one-quarter)

Si bought a plot of land for £17,000 and incurred purchase fees of £1,000. Si disposed of one-quarter of the field for proceeds of £30,000 and incurred expenses on disposal of £1,200. The remaining three-quarters of the plot of land was valued at £31,500.

Si subsequently sells the rest of the plot of land. 

Instructions: Calculate the acquisition cost for the disposal of the remaining land. Think about how you would approach this. 

9.3

(315000/30000+31500)*(17000+1000)=9219.5

The acquisition cost of the remainder of the land is £9,220, that is, the original cost of £18,000 less the cost of the part of the land sold as seen in the previous calculation (£8,780).

Sam disposed of a commercial lease for £250,000 during the current tax year. The lease was a 45-year lease when Sam acquired it 13 years ago for £114,500.  

The relevant lease percentages from the table in your rates sheet are: 

32 years	89.354
45 years	98.059

The lease cost for the lease disposed of, to use deduct in the calculation of Sam’s chargeable gain is calculated using the formula:

9.3

Diana disposed of a leasehold on a commercial building in December of last year for £170,000. The lease had 40 years to run at the date of disposal. It was acquired at a cost of £70,000 8 years previously when it had 48 years to run. 

The relevant lease percentages from the table in your rates sheet are:

40 years	95.457
48 years	99.289

Calculate the lease cost to be deducted in the calculation of the chargeable gain on Diana’s disposal.

9.3

The answer is £67,298.

Diana disposed of a leasehold on a commercial building in December of last year for £170,000. The lease had 40 years to run at the date of disposal. It was acquired at a cost of £70,000 8 years previously when it had 48 years to run. 

The relevant lease percentages from the table in your rates sheet are:

40 years	95.457
48 years	99.289

Calculate Diana’s chargeable gain on the disposal of the leasehold.

9.3

The answer is £102,702.

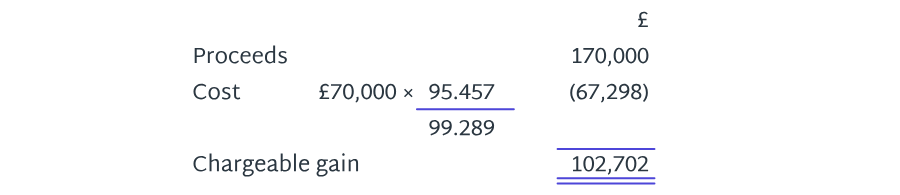
Which of the following is NOT considered an overhead cost in financial and management accounting?

1. Rent for office space

2. Direct material cost for a specific product

3. Machine maintenance expenses

4. Supervisor salaries

2.Direct material cost for a specific product

Direct material costs are associated with a specific product, so they are not classified as overheads. Overheads, on the other hand, include costs that cannot be attributed directly to a single product, such as rent, machine maintenance, or supervisor salaries.

Why is it important to include overhead costs when valuing stock in an organization?

1. To reduce overall stock valuation costs

2. To reflect the full cost of manufacturing or production

3. To allocate production overheads equally across all products

4. To simplify accounting processes

2.To reflect the full cost of manufacturing or production

Including overhead costs in stock valuation ensures that the stock reflects the complete cost it took to manufacture or produce, providing a more accurate picture of its value.

A company has just paid a dividend of 38p. It is expected that dividends will grow by 5% per annum and the required rate of return is 12%. 

Calculate the market value of a share in the company.

8.1

P = D (1 + g)／r - g 

= £0.38 × (1 + 0.05)／(0.12 - 0.05) 

= £5.70

Note: The top line of the fraction, D(1+g), represents next year’s dividend (ie the most recent dividend multiplied by one plus the growth rate). Also, because we put the value of the dividend into the formula in pounds, the answer we get out is also in pounds.

A company predicts that it will take 3 years to build up to its desired dividend of 30p. 

In year 1, it expects 15p, followed by 25p in year 2 before settling at 30p in year 3. Dividend growth thereafter will be 5% pa (per annum, ie each year). 

A required rate of return of 15% is expected. 

Calculate the value of a share in the company.

8.1

A company recently paid a dividend of £500,000 to their ordinary shareholders. The company expects a growth rate in dividends of 8% per annum and the market return for a competitor company in the same risk class is 14%. There are 250,000 shares in issue.

Calculate the value of our company:

a)  £7,777,777

b)  £8,333,333

c)  £9,000,000

d)  £9,500,000

8.1

• market value of the share

• times by number of shares

dividend paid = £500,000／250,000

The correct answer is c.

P = D(1 + g)／(r − g)

 

= (£500,000／250,000) x (1 + 0.08)／(0.14 − 0.08)

 

= £36

Value of company = £36 x 250,000 = £9,000,000

Note: An alternative approach would have been to use the total dividend of £500,000 on the top of the fraction rather than the £2 dividend per share. When using the total dividend on the top of the fraction, the answer it produces is the total price of the shares or, in other words, the value of the company.

A company has 500,000 £1 ordinary shares. Next year’s ordinary dividend is expected to be 60p.

Calculate the value of a share in this company if the required return is 10% and dividends are expected to grow at 3% per annum:

a)  £8.39

b)  £8.57

c)  £8.83

d)  £9.43

8.1

The correct answer is b.

Note - In this question, we are given next year’s dividend rather than the current year’s dividend. The 60p is equal to D(1 + g) and so there is no need to multiply by (1+ g).

P = D(1 + g)／(r − g)

= 60p / (0.10 − 0.03)

= £8.57

The shareholders of a company have just received a dividend of 8p per share in the current year.  This compares with a dividend of 7.5p in the previous year - a rate of growth that has been maintained over time.

Shareholders have a required rate of return of 9%.

Calculate the market value of a share in the company:

 

a)  £0.95

b)  £3.43

c)  £3.66

d)  £3.74

8.1

The correct answer is c.

Note: This question does not provide the dividend growth rate, but it can be calculated as shown below. 

g    = (8p - 7.5p)／7.5p = 6.67%

P = D(1 + g)／(r − g)

 

= £0.08 × (1 + 0.0667)／(0.09 − 0.0667)

 

= £3.66

The following information is available for a company:

	£
Ordinary share capital (£1 shares)	280,000
Most recent dividend paid	62,000

The expected dividend for next year is £65,500 and for the year after that is £70,100. Thereafter, dividends are expected to grow at 4% per annum.

Calculate the value of a share in the company if the required rate of return is 12%:

a)  £2.72

b)  £3

c)  £3.22

d)  £3.67

8.1

1. Present value of first 2 years’ dividends

Year	Dividend £	Dividend per share £	Discount factor	Present value £
1	65,500	0.23	0.8929	0.205
2	70,100	0.25	0.7972	0.199
				0.404

2. Future value of share at end of year 2

P = D(1 + g) / (r − g)

 

= £0.25 x (1 + 0.04) / (0.12 − 0.04)

 = £3.25

3. Present value of share

 

P = F／(1 + r)ⁿ

 

= £3.25／(1 + 0.12)²

 

 = £2.591

4. Total value

Value of a share today = £0.404 + £2.591 = £3

An investor holds £20,000 of 6% irredeemable preference shares in a company. 

If the investor’s required yield is 15%, calculate the value of the preference shares.

8.2

P = S／r 

= (£20,000 x 0.06)／0.15

= £8,000

An investor holds £20,000 of 6% redeemable preference shares in a company. The investor’s required yield is 15% and the shares are redeemable in 5 years’ time at their nominal value. 

 

The valuation of the shares is worked out by calculating the PV of the dividends in the first 4 years (the dividends available until redemption) and then calculating the PV of the redemption value (the original amount, £20,000, invested) plus the final coupon (dividend) in year 5 and adding these together:

8.2

Year	Cash flows £	Discount factors per rates sheet	Value £
1	20000×0.06=1,200	0.8696	1,044
2	1,200	0.7561	907
3	1,200	0.6575	789
4	1,200	0.5718	686
5	20000×0.06+dividend =21,200	0.4972	10,541
			13,967

An investor owns 20,000 £1 shares in a company’s 8% irredeemable preference shares. She requires a rate of return of 12%.

Calculate the value of her holding:

a) £13,333

b) £16,666

c) £20,667

d) £30,000

8.2

The correct answer is a.

 

P = S／r

= (£20,000 × 0.08)／0.12

= £13,333

An investor owns 20,000 8% preference shares in a company’s £1 preference shares, redeemable in 6 years’ time at their nominal value. He requires a rate of return of 12%.

Calculate the value of his holding:

a) £6,580

b) £11,095

c) £16,712

d) £23,699

8.2

The correct answer is c.

Year	Cash flows £	Discount factor	Value £
1	20,000 x 8%  = 1,600	0.8929	1,429
2	1,600	0.7972	1,276
3	1,600	0.7118	1,139
4	1,600	0.6355	1,017
5	1,600	0.5674	908
6	21,600	0.5066	10,943
			16,712

A lady inherited 20,000 9% preference shares with a nominal value of £1 each in a company. She is not sure whether to keep the shares and has asked you to provide a value for them. The shares are redeemable in 5 years’ time at a 6% premium.

Your client requires a rate of return of 11% on her investments.  

Calculate the current value of your client’s preference shares:

a) £17,614

b) £18,167

c) £18,523

d) £19,236

8.2

The correct answer is d.

Year	Cash flows £	Discount factor	Present value £
1	20,000 x 0.09  = 1,800	0.9009	1,622
2	1,800	0.8116	1,461
3	1,800	0.7312	1,316
4	1,800	0.6587	1,186
5	23,000*	0.5935	13,651
			19,236

 

* £1,800 + (£20,000 x 1.06) 

George has a holding of £10,000 of 10% redeemable debentures. The required rate of return on the stock exchange is 15%. The debentures are redeemable in 5 years’ time at a 4% premium to its nominal value. 

Calculate the value of the debentures.

8.2

The cumulative discount factor for years 1 to 4 can be calculated using the following formula (covered in Module 6): 

 

P = 1 – (1 + r)^{- n}／r

= 1 – (1 + 0.15)^{- 4}／0.15  

= 2.855 

 

Or 

 

by using the present discount factors from the relevant table:

Year	Cash flows £	Discount factors	Value £
1	1,000	0.8696	870
2	1,000	0.7561	756
3	1,000	0.6575	658
4	1,000	0.5718	572
5	11,400	0.4972	5,668
			8,524

If you wanted to, you could show year 5 on two separate lines and show the dividend and the face value separately, that is totally fine. Make sure you use the same discount rate for each of those parts.

Geoffrey has a holding of £30,000 of 9% redeemable debentures. The required rate of return on the stock exchange is 14%. The stock is redeemable in 20 years’ time at its nominal value. 

 

Calculate the value of the debentures using cumulative present value discount factors.

8.2

Year	Cash flows £	Cumulative discount factors	Value £
1–20	2,700	6.623	17,882
20	30,000	0.0728	2,184
			20,066

Remember that the cumulative discount factor can only be used where the same cash flow occurs in each year, starting in year 1. This means that the redemption value in year 20, a single cash flow, needs to be discounted separately from the remainder of the cash flows. 

Calculate the value of a holding of £25,000 of 12% redeemable debentures, when the required rate of return is 14% and the debentures are redeemable in 5 years’ time at their nominal value:

a)  £10,300

b)  £10,631

c)  £22,577

d)  £23,285

12.2

The correct answer is d.

Annual dividend = 0.12 × £25,000 = £3,000

Year	Cash flows	Discount factor	Present value
	£		£
1	3,000	0.8772	2,632
2	3,000	0.7695	2,309
3	3,000	0.6750	2,025
4	3,000	0.5921	1,776
5	28,000	0.5194	14,543
			23,285

An alternative solution using the cumulative discount factor would be:

Year	Cash flows	Discount factor	Present value
	£		£
1-4	3,000	2.914	8,742
5	28,000	0.5194	14,543
			23,285

A company issued £450,000 of 6% irredeemable bonds 3 years ago. Since then, interest rates have risen and the average market return for a similar bond is now 9%.

Calculate the value of the entire bond issue to an investor who wishes to match the market rate of return:

a)  £300,000

b)  £423,000

c)  £450,000

d)  £463,500

8.2

Incorrect

The correct answer is a.

P = S／r

= £450,000 × 0.06／0.09

= £300,000

What is the key difference between redeemable and irredeemable bonds or preference shares?

1. Redeemable securities provide permanent capital, while irredeemable securities do not

2. Irredeemable securities provide permanent capital, while redeemable securities involve repayment

3. Redeemable securities have no dividend payouts, while irredeemable securities do

4. There is no difference between the tw

8.2

b) Irredeemable securities provide permanent capital, while redeemable securities involve repayment

Which formula is used to calculate the value of irredeemable shares and bonds?

1. P = S/r

2. P = S × r

3. P = S + r

4. P = S ÷ (r × 2)

8.2

a) P = S/r

What does ‘S’ represent in the valuation formula for irredeemable shares and bonds?

1. Annual revenue

2. Annual dividend or interest

3. Total company assets

4. Total company liabilities

8.2

b) Annual dividend or interest

What approach is used to value redeemable shares and bonds?

1. Using the perpetuity formula

2. Calculating the present value (PV) of future cash flows and redemption value

3. Evaluating the company’s total net profit

4. Estimating the market share of the business

8.2

b) Calculating the present value (PV) of future cash flows and redemption value

As finance manager, you wish to calculate the cost of equity of your company. 

 

The following information is available:  

• Most recently paid dividend per share = 25p 

•  Share price = £4.20 

Dividends have increased by 6% per annum over the past few years. 

 

Calculate the cost of equity.

8.3

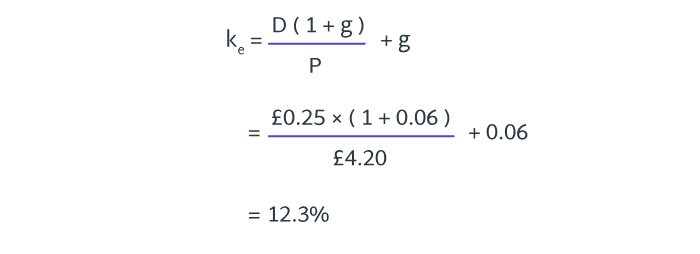
A company has just declared an ordinary dividend of 16p per share; the cum-div market price of an ordinary share is 200p. 

Calculate the company’s cost of equity capital, assuming a dividend growth rate of 10% per annum:

a) 18%

b) 18.7%

c) 18.8%

d) 19.6%

Note that the dividend of 16p is deducted from the cum-div market value of £2.00 when calculating "P" in the formula.

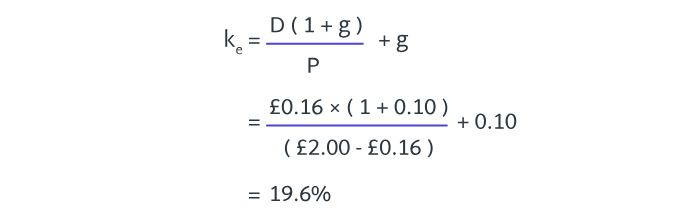
Identify which of the following statements in relation to dividends is/are TRUE:

• a) When the payment is made, it will be to all the shareholders who are on the company register on the record date.   

• b) The ex-dividend date is the date from which anyone buying a share is not entitled to the recently announced dividend;

• c) The price needed for calculating the cost of equity is the ‘cum-dividend’ price.

8.3

The correct answers are a and b.

You should take care with the price of a share in the cost of equity formula. The ‘ex-dividend’ price is required, and this is the price excluding any dividends which are about to be paid.

A company is about to pay a dividend of 24p on its 25p ordinary shares. The market value of a share is £3.

Calculate the company’s cost of equity if growth is anticipated at 4% for the foreseeable future, and assuming the ex-dividend date has not yet been reached:

a) 8.32%

b) 9.04%

c) 12.32%

d) 13.04%

8.3

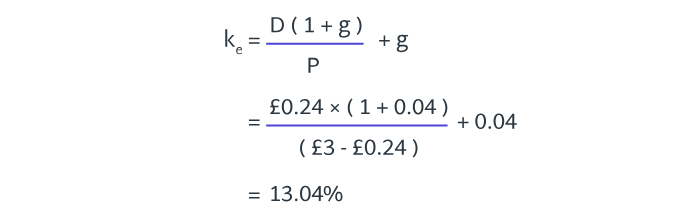
A company has just announced a dividend of 12p per share on its £1 ordinary shares. Currently, the market value of these shares is £1.89. Throughout the company’s life, the directors have consistently achieved annual dividend growth of 5%. 

Calculate the company’s cost of equity:

a) 6.5%

b) 11.5%

c) 12.1%

d) 13.4%

8.3

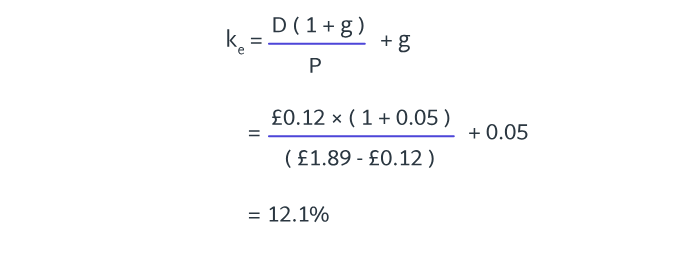
What is the ex-dividend date?

1. The date on which a company announces the upcoming dividend

2. The date from which buyers of shares are no longer entitled to the recently announced dividend

3. The date on which the dividend is paid

4. The date when shareholders vote on the dividend amount

8.3

Answer: B) The date from which buyers of shares are no longer entitled to the recently announced dividend

If you buy shares before the ex-dividend date, what is this known as?

1. Buying shares ex-dividend

2. Buying shares cum-dividend

3. Buying shares post-dividend

4. Buying shares at market price

8.3

Answer: B) Buying shares cum-dividend

What happens to the share price on the ex-dividend date?

1. It rises due to increased demand

2. It remains unchanged

3. It falls by the value of the dividend

4. It falls due to market uncertainty

8.3

Answer: C) It falls by the value of the dividend

Which shareholder receives the dividend?

1. The person who owns the shares on the announcement date

2. The person who owns the shares on the ex-dividend date

3. The person who buys the shares after the ex-dividend date

4. The person who sells the shares before the ex-dividend date

8.3

Answer: B) The person who owns the shares on the ex-dividend date

A company issues 8% £100 irredeemable bonds at a value of £80. 

 

The interest on the bonds is due to be paid soon and the company pays tax at 19%. 

 

Calculate the company’s cost of debt.

8.4

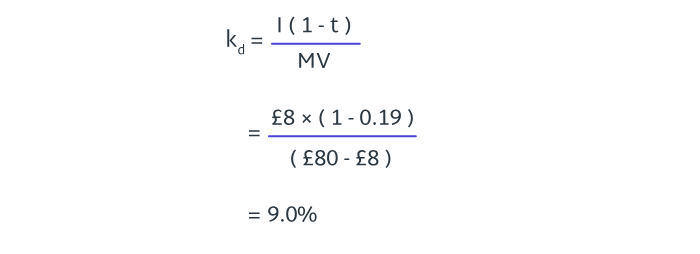
A company has issued 15% irredeemable debentures. The corporation tax rate is 25%. 

Calculate the cost of the debentures to the company if the debentures market value is identical to their nominal value:

a) 11.3%

b) 12.2%

c) 15%

d) 19%

8.4

assume £100 nominal value

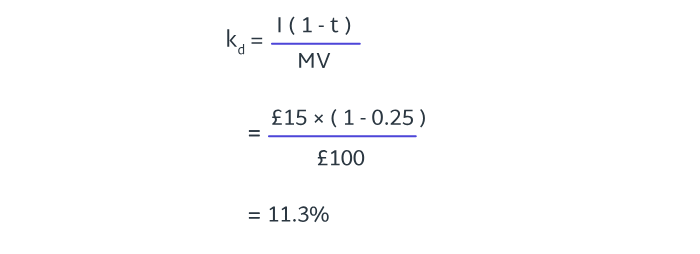
A company made profits before tax of £50m in the year ended 31 March 20X1, after charging interest on their 16.5% irredeemable debentures, and paid tax of £9.5m.  

Calculate the company’s cost of debt if the current market value of a debenture is £100:

a) 2.5%

b) 13.4%

c) 15.9%

d) 16.5%

8.48.4

Note: The tax rate can be approximated by dividing the actual tax paid in the year by the profits created in the year.

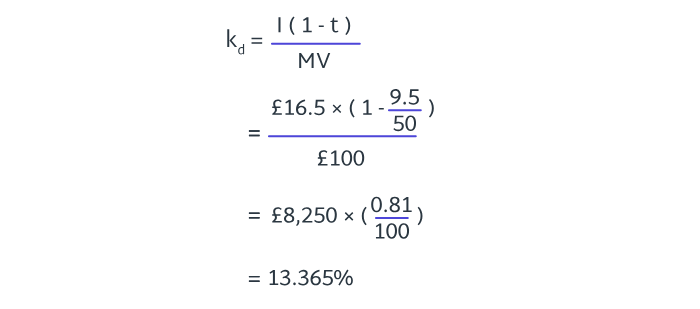
A company has redeemable 8% bonds in issue, currently trading at £96.77. These bonds are redeemable in 4 years’ time at par. 

 

Calculate the cost of debt for the bonds.

8.4

As discount rates have not been given, choose an initial discount rate as a starting point, say 10%.

Description	Amount (£)	DF @ 10%	PV (£)
Market Value	(96.77)	1	(96.77)
Interest	8	0.9091	7.27
Interest	8	0.8264	6.61
Interest	8	0.7513	6.01
Interest	8	0.6830	5.46
Redemption	100	0.6830	68.30
			(3.12)

You now look at what the Net Present Value (NPV) is. Is it positive or is it negative? In this example, with a discount rate of 10%, we have a negative NPV.

The negative NPV indicates that the rate we’re looking for is lower than 10%. So, we’ll make a guess, let’s guess at 8% (you may have chosen any rate that is less than 10%):

Year	Description	Amount (£)	DF @ 8%	PV (£)
0	Market Value	(96.77)	1	(96.77)
1	Interest	8	0.9259	7.41
2	Interest	8	0.8573	6.86
3	Interest	8	0.7938	6.35
4	Interest	8	0.7350	5.88
4	Redemption	100	0.7350	73.50
NPV				3.23

A company is issuing 7% redeemable debentures at par. The debentures are redeemable in 15 years at a value of £195 each. 

Calculate the cost of debt, using discount rates of 8% and 12%:

a) 5.6%

b) 6.7%

c) 9.1%

d) 10.2%

8.4

Year	Cash flow £	Discount factor at 8% rate sheet	Present value at 8% £	Discount factor at 12%	Present value at 12%
0	(100)	1.0000	(100)	1.0000	(100)
1-15	7	8.559	59.91	6.811	47.68
15	195	0.3152	61.46	0.1827	35.63
			21.37		(16.69)

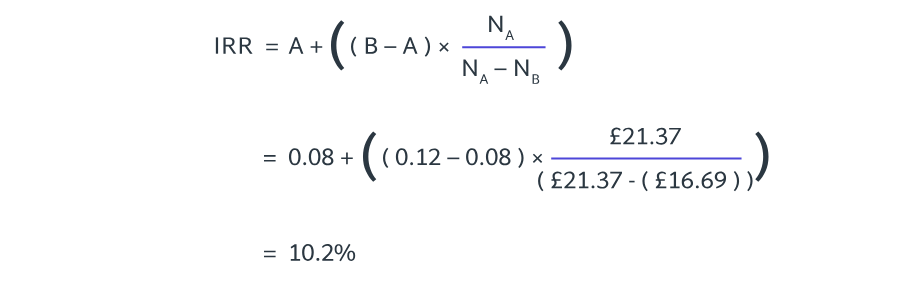
A company finances some of its operations with debt in the form of 7% debentures. These were issued at 95% of their nominal value 4 years ago and are redeemable at a 3% premium in 4 years’ time. They are currently trading at exactly their nominal value.

Calculate the cost of debt for these debentures, using an initial discount rate of 10% and ignoring all taxation:

a) 6.8%

b) 7.8%

c) 9.3%

d) 12.4%

The correct answer is b.

Year	Cash flow £	Discount factor at 10%	Present value at 10% £	Discount factor at 5%	Present value at 5% £
0	(100)	1.0000	(100.00)	1.0000	(100.00)
1	7	0.9091	6.36	0.9524	6.67
2	7	0.8264	5.78	0.9070	6.35
3	7	0.7513	5.26	0.8638	6.05
4	7 + 103 = 110	0.6830	75.13	0.8227	90.50
			(7.47)		9.57

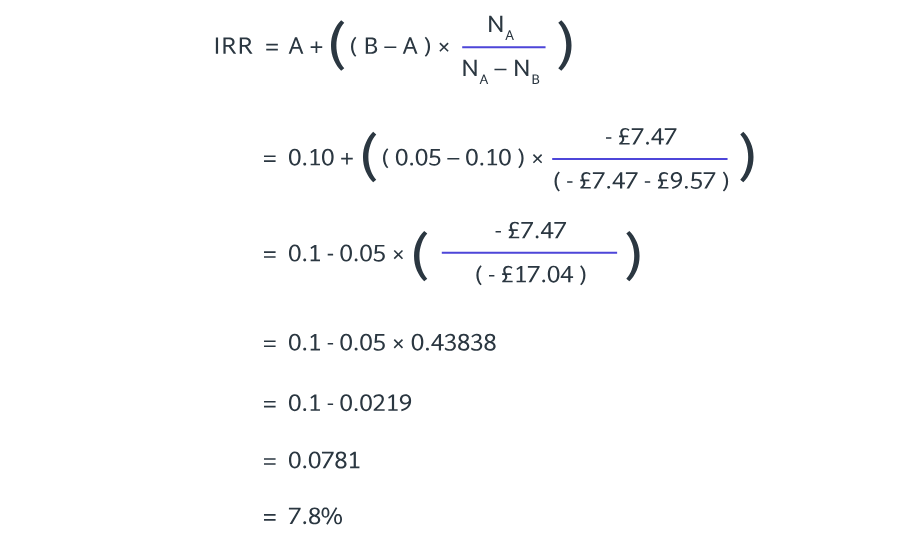
Why is the cost of debt generally lower than the cost of equity?

1. Debt financing is riskier than equity financing

2. Interest payments on debt are tax-deductible, whereas dividends are not

3. Debt holders receive payments after equity holders in case of liquidation

4. Issuing debt financing is more expensive than issuing equity financing

8.4

Answer: B) Interest payments on debt are tax-deductible, whereas dividends are not

What does an 8% bond mean?

1. The bond pays 8% of its market value as interest

2. The bond pays 8% of its nominal value (£100) as interest

3. The bond pays 8% of the company’s profits as interest

4. The bond pays 8% of the total debt issued by the company

8.4

Answer: B) The bond pays 8% of its nominal value (£100) as interest

Which of the following is NOT a reason why debt financing is cheaper than equity financing?

1. Debt holders rank before equity holders in case of liquidation

2. Debt financing is quicker and easier to issue than equity financing

3. Debt financing does not require interest payments

4. Debt is a less risky investment than equity

8.4

Answer: C) Debt financing does not require interest payment

What is the ex-interest price of a bond?

1. The market price including any interest that is about to be paid

2. The market price excluding any interest that is about to be paid

3. The nominal value of the bond

4. The price at which the bond was originally issued

8.4

Answer: B) The market price excluding any interest that is about to be paid

How is the cost of redeemable debt calculated?

1. Using the dividend discount model

2. Using the internal rate of return (IRR) of the cash flows

3. Using the price-to-earnings ratio

4. Using the debt-to-equity ratio

8.4

Answer: B) Using the internal rate of return (IRR) of the cash flow

In this example, we have a company which has both debt and equity in its capital structure. The cost of equity and cost of debt calculations have already been completed for us.

A company whose cost of equity is 12% and cost of debt is 6.5% has 80% of its total capital in the form of equity and 20% of its total capital in the form of debentures.

Calculate its weighted average cost of capital.

Note: You can see here the usual scenario of debt being cheaper than equity.

The weighted average cost of capital is calculated to be 10.9%. A quick sense check here shows this as reasonable – we expect the average cost of capital to be between 6.5% and 12%, but nearer to the 12% cost of equity figure as most of the company's capital is in the form of equity

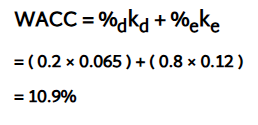
A company’s shares are currently trading at £5.30 each, with a dividend of 60p per share about to be paid (the ex-dividend date has not yet been reached). This maintains a dividend growth rate of 6%, which the company has seen over the past few years and is expected to extend into the future. 

 

Company A also has irredeemable bonds in issue which are trading at £112 each. These bonds carry a coupon of 7% and interest has just been paid. The tax rate is 25%.

 

The following information is available in the most recent statement of financial position:

	£'000
Share Capital (Ordinary 50p Shares)	1,400
7% Irredeemable Bonds	700

Calculate the company’s weighted average cost of capital.

8.5

There are a number of steps that need to be taken to arrive at the company’s WACC.

Step 1:

Firstly, you need to calculate the company’s cost of equity and the cost of debt. We will start with the company’s cost of equity using the formula we know from before:

The main thing to notice about this question is that the £5.30 is the ‘cum-dividend’ price as a dividend is about to be paid but the ex-dividend date has not yet been reached. So, we need to subtract the upcoming dividend of 60p to calculate the ex-dividend value.

Step 2:

Now we will calculate the company’s cost of debt.

The debt is in the form of irredeemable bonds, and so we are using the formula:

Interest has just been paid so the value of £112 is the ex-interest value we need; it doesn’t require adjustment.

Step 3: 

We need the weightings/proportion of debt to equity before we can calculate the WACC.

This example does not provide the weightings of the market values of debt and equity in the capital structure, but this can be calculated from the statement of financial position information as follows:

• Number of ordinary shares
  = £1,400,000 / £0.50 = 2,800,000

• Market value of ordinary shares (ex-dividend)
  = 2.8m x (£5.30 - £0.60) = £13,160,000

• Number of bonds
  = £700,000 / £100 = 7,000 

• Market value of bonds 
  = 7,000 x £112 = £784,000

	Market value	Percentage value
Ordinary shares	£13,160,000	94.4%
Bonds	£784,000	5.6%
Total	£13,944,000	100%

The "percentage value" represents the weighting of each source of capital in the company's capital structure. For example, for bonds, it is calculated as: £784,000 / £13,944,000 = 5.6%.

Step 4:                                                                  

The WACC can now be calculated as:

WACC = %_dk_d + %_ek_e
= (0.056 x 0.047) + (0.944 x 0.195)
= 18.7%

A company is financed 75% by equity and 25% by debt. 

The shares are trading at £5.20 cum dividend, with a dividend of 60p about to be paid. Dividends are growing at 3% per year.

The company also has 9% irredeemable debt in issue which is currently trading at £85. The company pays tax at a rate of 19%.

Calculate the company's weighted average cost of capital.

8.5

Step 1 - cost of equity:

Step 2 - cost of debt:

Step 3:

We need the weightings of equity vs debt (given in the question).

Step 4 - calculate the WACC:

WACC = %_dk_d + %_ek_e
= (0.25 x 0.086) + (0.75 x 0.164)
= 14.5%

A company's shares are trading at £2.50 ex-dividend. The most recent dividend was 25p per share, and dividends have been growing at a rate of 5% per year.

The same company pays 6% interest on its debt financing which is redeemable at a 4% premium in 3 years' time. These bonds are currently trading at £86 ex-interest.

The following lines appear on the company's Statement of Financial Position:

£1 ordinary shares	£51,600
Redeemable debentures	£100,000

Calculate the WACC (ignoring the effects of taxation). You should use 10%  and/or 15% for  any discounting calculations.

8.5

Step 1 - cost of equity:

Step 2 - cost of debt: debt:

Year	CF	PV @ 10%	PV @ 15%
0	(86.0)	(86.0)	(86.0)
1	6	5.45	5.22
2	6	4.96	4.54
3	104 + 6	82.64	72.33
		7.05	(3.91)

Step 3 - we need the weightings of equity vs debt: 

				Market value	Percentage value
MVe	=	51,500 x £2.50	=	£129,000	60%
MVd	=	£100,000 x 86/100	=	£86,000	40%
				£215,000	100%

Step 4 - calculate the WACC:

WACC = %_dk_d + %_ek_e
= (0.6 x 0.155) + (0.4 x 0.132)
= 14.6%

A company is financed by one million £1 ordinary shares and £600,000 of 8% debentures. The market values are £1.40 and £90 respectively. A dividend of 14p has just been paid and dividends have been growing at 6% per annum. Interest is shortly to be paid on the debentures, which are irredeemable.

Calculate the company’s weighted average cost of capital, ignoring all taxation:

a) 9.8%

b) 14.8%

c) 15.9%

d) 16.6%

8.5

The correct answer is b.

A company is financed by a mixture of debt and equity. The company’s 8% bonds, with a book value of £400,000, are redeemable at par in 4 years, and are currently trading at 95%. The company also has two million £1 ordinary shares, currently trading at £1.10. The cost of equity has been calculated as 16%.

Calculate the company’s weighted average cost of capital, ignoring all tax:

a) 13.8% 14.9%

c) 15.1%

d) 16%

8.5

The correct answer is c.

Note: The cost of redeemable debt requires an IRR calculation, but no discount rates have been provided. You should select sensible discount rates but may calculate a slightly different figure depending on the ones chosen. In the exam, it will not be possible to get a question wrong purely through choice of appropriate discount rates. 

Cost of debt calculation:

Year	Cash flow	Discount factor at 5%	Present value at 5%	Discount factor at 10%	Present value at 10%
0	(380,000)	1.0000	(380,000)	1.0000	(380,000)
1	32,000	0.9524	30,477	0.9091	29,091
2	32,000	0.9070	29,024	0.8264	26,445
3	32,000	0.8638	27,642	0.7513	24,042
4	432,000	0.8227	355,406	0.6830	295,056
			62,549		(5,366)

You can view the formula for IRR below.

K_d = IRR = 5% + (10% - 5%) x (62,549 / (62,549 + 5,366)
= 5% + (5% x (62,549 / 67,915))

= 9.6%

 

Cost of equity calculation:

Given in the question = 16%

 

Weightings for equity vs debt:

				Market value	Percentage value
MVd	=	0.95 x £400,000	=	£380,000	14.7%
MVe	=	2m x £1.10	=	£2,200,000	85.3%
				£2,580,000	100%

 

WACC calculation:

WACC = %_dk_d + %_ek_e

= (14.7% x 0.096) + (85.3% x 0.16) = 1.411% + 13.648%

= 15.1%

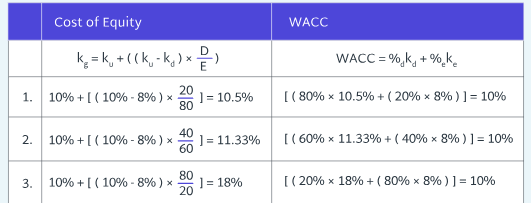
An ungeared firm had a cost of capital of 10%. The firm is about to issue 8% bonds but is unsure yet what proportion of their capital structure will be made up of these bonds. 

 

Using the MM theory (without tax), calculate the firm’s WACC under each of the following capital structures:

• 80% equity 20% debt

• 60% equity 40% debt

• 20% equity 80% debt

8.6

A company is currently purely financed by equity with a market value of £450,000. The cost of equity in this ungeared position, K_u, is 18%. The company is considering introducing gearing into the company by taking out an 8% bank loan of £250,000.

Calculate the company’s resulting weighted average cost of capital if it takes out this loan, following the Modigliani-Miller theory of capital structure (without tax):

a) 10.9%

b) 16.7%

c) 18.0%

d) 23.6%

8.6

The correct answer is c.

WACC remains constant under the Modigliani-Miller theory without tax, so no calculation is needed, although the correct calculation also leads to the same answer.

A company is currently financed solely by 150,000 shares, priced at £3.80 each. The company’s cost of capital is currently 15%. 

The company plans to issue 3,000 £100 irredeemable bonds. These bonds will pay interest at 6% per annum, with the market value expected to be £108 based on current market conditions.

Calculate the company’s cost of equity after these bonds are issued, following the Modigliani-Miller theory of capital structure (without tax):

a) 19.74%

b) 19.97%

c) 20.12%

d) 20.37%

8.6

The correct answer is d.

Rella Ltd (Rella) is an ungeared firm with a cost of equity of 15%.

 

If Rella issues 6% debenture stock such that it has a capital structure of 60% equity and 40% debt and the tax rate is 19%, calculate:

1. The cost of equity using the MM formula (with tax)

2. WACC

8.6

Note: Be careful with the treatment of the tax. We are deducting tax in Modigliani-Miller’s cost of equity formula, but then we also need to remember to take account of tax in the cost of debt calculation in the usual way, just like we did back earlier in the module.

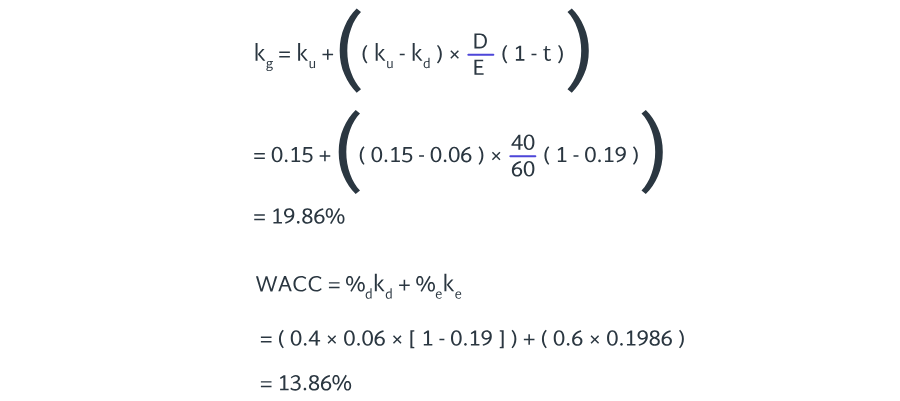
An ungeared firm has share capital with a market value of £750,000 and a cost of equity of 12%. It is considering issuing £250,000 10% debentures and pays tax at a rate of 25%.  

Calculate the firm’s weighted average cost of capital, using Modigliani-Miller’s theory (with tax):

a) 10.9%

b) 11.3%

c) 11.7%

d) 11.9%

8.6

The correct answer is b.

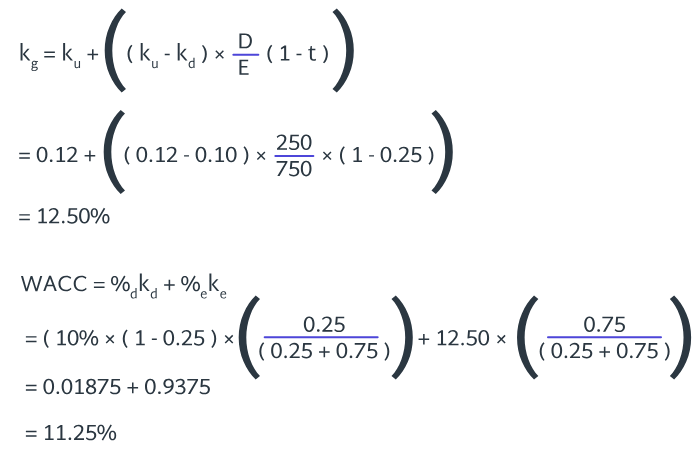
Incense Ltd (Incense) pays tax at a rate of 19% and currently has a cost of capital of 14%. The company is considering issuing debt with a market value of £500,000 and associated interest cost of 5%. This would be the company’s first use of debt financing, as it is currently financed purely by shares with a market value of £2.5m. 

Following the Modigliani-Miller theory of capital structure (with tax), calculate Incense’s weighted average cost of capital, assuming the debt issue goes ahead:
a) 11.4%

b) 13.6%

c) 14%

d) 15.3%

8.6

The correct answer is b.

McGlynn's new machine would cost £10,000 and will be scrapped after 5 years. The cash flows for the machine are listed here:

Year	Cash inflow £
1	6,000
2	5,000
3	4,000
4	3,000
5	1,000

Calculate the payback period for McGlynn.

9.1

Year	Net cash flow £	Cumulative  net cash flow £
0	(10,000)	(10,000)
1	6,000	(4,000)
2	5,000	1,000

Therefore, the payback period is at some point during year 2. With £4,000 outstanding at the start of the year and £5,000 received, it will be paid off after 1 year plus £4,000/£5,000 = 0.8 years. (0.80 x 12months = 10 months). therefore, approximately 1 year and 10 months.

A company is considering investing in a project. The project is predicted to last 5 years and the initial cost of the equipment is £30,000. The equipment will have a residual value of £6,000 and will be depreciated on a straight-line basis. The company has a cost of capital of 8%.

Excluding the amounts above, the operational net cash flows for the 5 years are:

Year	Cash flow £
1	6,000
2	9,000
3	(1,000)
4	12,000
5	11,000

Calculate the payback period of the project to the nearest month:

a) 3 years and 10 months

b) 4 years and 2 months

c) 4 years and 4 months

d) 4 years and 8 months

9.1

The correct answer is c.

Year	Cash flow £	Cumulative cash flow £
0	(30,000)	(30,000)
1	6,000	(24,000)
2	9,000	(15,000)
3	(1,000)	(16,000)
4	12,000	(4,000)
5	17,000	13,000

Payback occurs in year 4. Fraction of the year calculated as follows:

£4,000／£11,000 × 12 = 4.4 months

So, payback period is 4 years and 4 months to the nearest month.

Note: The information provided about the depreciation and the cost of capital were not needed for this question and were there to mislead/distract (preparing you for exam questions). So please be careful of this.

The directors of a company are planning to acquire a new piece of machinery. The machine will cost £46,500, and the net cash flows (excluding the purchase price) arising as a result of its operation are as follows:

Year	Cash flow £
1	11,000
2	6,500
3	10,000
4	24,000
5	10,500

At the end of the 5-year period over which the machine will be held, it will be sold for £5,000 (not included in the net cash flows above). The company has a policy of depreciating its machinery on a straight-line basis over its useful economic life. 

The company’s cost of capital has been calculated as 9%.

Calculate the payback period for the machinery to the nearest month:

a) 3 years and 2 months

b) 3 years and 10 months

c) 4 years and 2 months

d) 4 years and 10 months

9.1

The correct answer is b.

Year	Cash flow £	Cumulative cash flow £
0	(46,500)	(46,500)
1	11,000	(35,500)
2	6,500	(29,000)
3	10,000	(19,000)
4	24,000	5,000
5	15,500	20,500

Payback occurs in year 3. Fraction of the year calculated as follows:

£19,000／£24,000 × 12 = 9.5 months

Payback will be in 3 years and 10 months to the nearest month.

Note: The information provided about the residual value, the depreciation and the cost of capital were not needed for this question and were there to mislead/distract (preparing you for exam questions); the information was a bit of a ‘red herring’! So please be careful of this.

Remember, the machine would be bought for £10,000 and depreciated over 5 years with no residual value. Cash flow and other relevant figures are also included below:

Year	Cash flow £	Depreciation £	Profit/(Loss) £
1	6,000	(2,000)	4,000
2	5,000	(2,000)	3,000
3	4,000	(2,000)	2,000
4	3,000	(2,000)	1,000
5	1,000	(2,000)	(1,000)

Calculate the ARR for McGlynn's new machine. Give it a go before you look at the solution. 

9.2

The table above and calculation below show that the average annual profit is £1,800. This will make up the top of the ARR calculation (we will show you two ways of performing the ARR calculation directly below and at the end of the solution).

 

 Annual average profits = £4,000 + £3,000 + £2,000 + £1,000 - £1,000／5 years 

 

= £1,800 (these figures are shown in the table above)

 

The capital investment is £5,000.

Average capital cost = ½ (investment + residual value)

= ½ (10,000) + 0)

= £5,000

Using these figures in the ARR calculation, results in an ARR of 36%.

Therefore: ARR = £1,800／£5,000 x 100 = 36%

Alternatively, you can lay out your calculation for AAP as below, both give the same answer:

AAP = (total cash flow less depreciation)／useful life

Average annual profits = (£6,000 + £5,000 + £4,000 + £3,000 + £1,000) / 5

= £3,800

Less depreciation =   £10,000 / 5 

= £2,000 

AAP = £3,800 - £2,000

= £1,800 

The finance manager of a company uses the accounting rate of return (ARR) method of investment appraisal and depreciates plant and machinery on a straight-line basis. She is considering spending £35,000 on a machine at the end of 20X2, which will generate additional net operating cash flows (excluding the above amounts) as follows:

Year	Cash flow £
20X3	20,000
20X4	18,000
20X5	15,000
20X6	8,000
20X7	8,000
20X8	5,000

It is estimated that the residual value of the machine at the end of its useful life will be £4,000. 

Calculate the ARR of this investment:

a) 33.3%

b) 36.7%

c) 46.2%

d) 63.2%

9.2

Year	Cash flow £	Depreciation £
20X3	20,000	5,167
20X4	18,000	5,167
20X5	15,000	5,167
20X6	8,000	5,167
20X7	8,000	5,167
20X8	5,000	5,167
Average	12,333	5,167

Annual depreciation = (£35,000 – £4,000) / 6 = £5,167

ARR = Average annual profits (AAP) / Average capital investment (ACI)

= (£12,333 − £5,167) / (½ x (£35,000 + £4,000))

= 36.7%

Alternatively, you can lay out your calculation as below, both give the same answer:

The finance manager of a company wishes to appraise an investment which costs £60,000 and will have a residual value of £4,000 after its useful life of 5 years. The asset purchased will be depreciated on a straight-line basis.

Excluding the amounts above, the net cash flows arising from the investment are as follows:

Year	Cash flow £
1	22,000
2	20,000
3	19,000
4	5,000
5	4,000

Calculate the accounting rate of return of the investment:

a) 8.75%

b) 9.33%

c) 10%

d) 43.75%

9.2

The correct answer is a.

The finance manager of a company wishes to appraise an asset that costs £740,000, has a useful economic life of 4 years and a residual value of £110,000. The asset purchased will be depreciated on a straight-line basis. The company has a policy of selling assets at the end of their useful economic lives.

Excluding the amounts above, the net cash flows arising from the investment are as follows:

Year	Cash flow £
1	145,000
2	230,000
3	238,000
4	240,000

Calculate the accounting rate of return on the investment:

a) 13.1%

b) 15.1%

c) 17.7%

d) 50.2%

9.2

The correct answer is a.

Identify which of the following statements is/are CORRECT in relation to the accounting rate of return (ARR) technique of investment appraisal: 

• a) If an investment has no residual value, the average capital investment used in calculating the ARR is found by dividing the initial investment value by two.

• b) ARR ignores the depreciation policy of the business.

• c) ARR is a measure that considers cash flows but not profits.  

9.2

The correct answers is a 

Calculate the NPV for McGlynn’s new machine.

 

Remember that discounting can be done with either the discount tables or formulae introduced in Module 6. For the example, we have provided the cash flow and discount figures below to get you started (do please refresh your memory and ensure you can obtain these yourself). 

Remember in this example we told you the McGlynn has a cost of capital of 20%. We can use our discount tables to work out the present value factors for each of the years. To calculate the present value we take the cash flow and multiply it by the present value factor. 

 

Try working out the present value yourself, add the total and see if McGlynn should buy the machine: 

Year	Cash flow £	20% discount factors	Present value £
0	(10,000)	1
1	6,000	0.8333
2	5,000	0.6944
3	4,000	0.5787
4	3,000	0.4823
5	1,000	0.4019
			NPV = ?

Note: NPV, similar to the payback calculation, ignores depreciation. It considers the cashflow implications of a project, rather than the accounting profits after depreciation. It is also important to note that if you are provided with the residual value of the asset, you should include it in your cash flows as an inflow in the final period.

9.3

Year	Cash flow £	20% discount factors	Present value £
0	(10,000)	1	(10,000)
1	6,000	0.8333	5,000
2	5,000	0.6944	3,472
3	4,000	0.5787	2,315
4	3,000	0.4823	1,447
5	1,000	0.4019	402
Net present value =			2,636

When you complete the table and add up all the present value figures, you see that the NPV for McGlynn's project is positive, and therefore the project should be accepted as it will increase shareholder value.

It is 1 February 20X6 and a company is appraising an investment opportunity which is forecast to generate annual net cash inflows of £12,000 each year for 10 years. The investment, which is due to commence on 1 February 20X7, will require a capital outlay of £50,000 on this day. The first net cash inflow will be received on 1 February 20X8. The investment will have no residual value and will cost £10,000 to dismantle the year after the revenues finish. 

The company’s cost of capital is 9%. 

 

Calculate the net present value of the investment opportunity: 

a) £17,098

b) 21,228

c) 24,783

d) 29,049

9.3

Note: This question is different from many others in that the investment does not begin immediately. The initial investment in this question takes place 1 year into the future, and so must be discounted by 1 year. The first cash inflow is received 2 years from now, and so on.  

Year	Cash flow £	9% discount factor	Present value £
0 (Feb 20X6)	-	1.000	-
1 (Feb 20X7)	(50,000)	0.9174	(45,870)
2 (Feb 20X8)	12,000	0.8417	10,100
3	12,000	0.7722	9,266
4	12,000	0.7084	8,501
5	12,000	0.6499	7,799
6	12,000	0.5963	7,156
7	12,000	0.5470	6,564
8	12,000	0.5019	6,023
9	12,000	0.4604	5,525
10	12,000	0.4224	5,069
11	12,000	0.3875	4,650
12	(10,000)	0.3555	(3,555)
NPV			21,228

The NPV is positive and therefore the company should proceed with the investment opportunity.

Alternatively, the cumulative discount factor can be used for the repeated cash flows in years 2 to 11 as the figure for years 1 to 11 of 6.805, less the year 1 figure of 0.917, is to equal 5.888.

Try working out the present value yourself, add the total and see if McGlynn should buy the machine: 

Year	Net cash flows (considering 25% tax) £	20% discount factors	Present value £
0	(10,000)	1
1	6,000 x (1 - 0.25)	0.8333
2	5,000 x (1 - 0.25)	0.6944
3	4,000 x (1 - 0.25)	0.5787
4	3,000 x (1 - 0.25)	0.4823
5	1,000 x (1 - 0.25)	0.4019
			NPV = ?

9.3

Year	Net cash flows £	20% discount factors	Present value £
0	(10,000)	1	(10,000)
1	6,000 x 0.75 = 4,500	0.8333	3,750
2	5,000 x 0.75 = 3,750	0.6944	2,604
3	4,000 x 0.75 = 3,000	0.5787	1,736
4	3,000 x 0.75 = 2,250	0.4823	1,085
5	1,000 x 0.75 = 750	0.4019	301
Net present value =			(524)

The finance manager of a company wishes to appraise an asset that costs £300,000, with a useful economic life of 4 years and no residual value.   

 

Excluding these amounts, the net pre-tax cash flows arising from the investment are as follows: 

Year	Cash flow £
1	135,000
2	90,000
3	114,000
4	120,000

The company pays tax on the pre-tax net cash flows (but not the initial investment cost) at a rate of 25%, payable in the year incurred, and has calculated its weighted average cost of capital to be 7%. 

 

Calculate the net present value of the investment: 

a) £(16,824)

b) £(7,962)

c) £67,037

d) £89,383

9.3

The correct answer is b.

Year	Cash flow £	Discount factor	Present value £
0	(300,000)	1.0000	(300,000)
1	135,000 x (1 - 0.25) = 101,250	0.9346	94,628
2	90,000 x (1 - 0.25) = 67,500	0.8734	58,955
3	114,000 x (1 - 0.25) = 85,500	0.8163	69,794
4	120,000 x (1 - 0.25) = 90,000	0.7629	68,661
NPV			(7,962)

The finance manager of a company wishes to appraise an investment which costs £40,000, has a useful economic life of 4 years and no residual value. The company pays tax on its net revenue cash flows at a rate of 25%, payable in the year incurred, and uses a discount rate of 6% in investment decisions. 

 

The pre-tax net cash flows arising from the investment (which exclude the amounts above) are as follows: 

Year	Cash flow £
1	12,500
2	15,000
3	17,500
4	15,000

Calculate the net present value of the investment: 

a) £(2,116)

b) £(1,212)

c) £8,788

d) £11,718

9.3

The correct answer is b.

Year	Cash flow £	Discount factor	Present value £
0	(40,000)	1.000	(40,000)
1	12,500 x (1 - 0.25) = 9,375	0.9434	8,844
2	15,000 x (1 - 0.25) = 11,250	0.8900	10,013
3	17,500 x (1 - 0.25) = 13,125	0.8396	11,020
4	15,000 x (1 - 0.25) = 11,250	0.7921	8,911
			(1,212)

A financial manager is considering the purchase of a piece of equipment at a cost of £230,000. The equipment will be used for 5 years before being scrapped with no residual value. The equipment would be depreciated over its useful life using straight-line depreciation.  

 

Excluding the amounts above, the net cash flows (before tax) associated with the equipment will be:

Year	Cash flow £
1	80,000
2	60,000
3	45,000
4	35,000
5	30,000

The company’s cost of capital is 10% and tax is paid on revenue cash flows at 19% (all tax payments are made the year after the tax is incurred). 

 

Calculate the net present value of the investment: 

a) £(25,390)

b) £(31,344)

c) £(65,660)

d) £69,090

Note: Although the equipment has a useful life of 5 years, tax is paid a year in arrears and so 6 years are required in the NPV calculation.  

The correct answer is c.

Year	Cash flow £	Discount factor	Present value £
0	(230,000)	1,000	(230,000)-
1	80,000	0.9091	72,728
2	60,000 – (80,000 x 0.19) = 44,800	0.8264	37,023
3	45,000 – (60,000 x 0.19) = 33,600	0.7513	25,244
4	35,000 – (45,000 x 0.19) = 26,450	0.6830	18,065
5	30,000 – (35,000 x 0.19) = 23,350	0.6209	14,498
6	– (30,000 x 0.19) = (5,700)	0.5645	(3,218)
			(65,660)

Note: As all tax payments are made the year after the tax is incurred, if we take year 2 as an example: our cash flow is £60,000 but we must pay tax on year 1 cash flows, so the net amount of cash flow is £44,800.9.3

Identify which of the following statements is/are CORRECT in relation to methods of capital investment appraisal: 

1. The accounting rate of return of a project expresses the average cash flows as a proportion of the average capital investment (calculated as ½ (investment - residual value)). 

2. Although it gives a figure for the absolute gain in shareholder wealth, one of the main disadvantages of the net present value method is that those without financial knowledge find it difficult to understand. 

a) 1 only
b) 2 only
c) Both of the above
d) Neither of the above

9.3

The correct answer is b. 

The accounting rate of return of a project expresses the average profits as a proportion of the average capital investment (calculated as ½ (investment + residual value)).

The finance manager of a company wishes to appraise an investment that costs £220,000, with a residual value of £20,000 after its useful life of 4 years. The asset purchased will be depreciated on a straight-line basis. 

 

Excluding the amounts above, the net cash flows arising from the investment are as follows: 

Year	Cash flow £
1	88,000
2	80,000
3	76,000
4	60,000

 

Calculate the internal rate of return of the investment, using discount rates of 14% and 20%: 

a) 12.26%

b) 15.41%

c) 18.02%

d) 25.79%

9.4

ar	Cash flow £	Discount factor at 14%	Present value at 14% £	Discount factor at 20%	Present value at 20% £
0	(220,000)	1.0000	(220,000)	1.0000	(220,000)
1	88,000	0.8772	77,194	0.8333	73,330
2	80,000	0.7695	61,560	0.6944	55,552
3	76,000	0.6750	51,300	0.5787	43,981
4	80,000	0.5921	47,368	0.4823	38,584
NPV			17,422		(8,553)

Note: The cash flow in year 4 is the £60,000 cash flow + £20,000 cash flow residual value = £80,000. The question tells us the residual value of the equipment and that the useful life is 4 years. If the question provides you the information about residual value, you should assume the equipment will be sold at the end of the project and this cash flow should be included in your NPV calculation.

Image 4.3

Accessible text of image(opens in a new tab)

A project has the following net cash flows: 

Year	Cash flow £
0	(40,000)
1	15,000
2	15,000
3	15,000
4	15,000

 

The company discovered that the cash flow in year 4 had been over-estimated.  

 

Calculate the effect of correcting this over-estimation on the project’s internal rate of return (IRR) and payback period: 

a) IRR = Decreases. Payback period = No change

b) IRR = Decreases. Payback period = Increases

c) IRR = Increases. Payback period = No change

d) IRR = Increases. Payback period = Increases

9.4

Year	Cash flow £	Cumulative cash flow £
0	(40,000)	(40,000)
1	15,000	(25,000)
2	15,000	(10,000)
3	15,000	5,000
4	15,000	20,000

Payback occurs between the end of year 2 and the end of year 3 so is unaffected by a change in the year 4 cash flow.  

Correcting the IRR leads to a smaller cash flow in year 4, which lowers the return on the project. In other words, the IRR decreases.  

A company is involved in the wholesale purchase and resale of wine. The company is planning to buy a new loading machine at a cost of £6,000. It plans to use the machine for 5 years before selling it. The residual sales proceeds are forecast to be £1,000. The company depreciates machinery on a straight-line basis over its useful economic life and has a rate of return of 5%. 

 

Excluding these sums, the net cash flows associated with the machine are as follows:

Year	Cash flow £
1	2,000
2	1,200
3	1,500
4	1,600
5	2,000

 

Calculate the internal rate of return of the project, using discount rates of 10% and 14%: 

a) 11.82%

b) 13.28%

c) 14.06%

d) 15.12%

9.4

Year	Cash flow	Discount factor at 10%	Present value £	Discount factor at 14%	Present value £
0	(6,000)	1.0000	(6,000)	1.0000	(6,000)
1	2,000	0.9091	1,818	0.8772	1,754
2	1,200	0.8264	992	0.7695	923
3	1,500	0.7513	1,127	0.6750	1,013
4	1,600	0.6830	1,093	0.5921	947
5	3,000	0.6209	1,863	0.5194	1,558
NPV			893		195

Image 4.4

Accessible text of image(opens in a new tab)

Wayne owns a number of stores and is looking to invest in an additional shop with an upfront cost of £50,000 to cover the next 6 years. Excluding this amount, the following net cash flows are expected to be generated over that period: 

Year	Cash flow £
1	10,500
2	12,000
3	15,500
4	16,500
5	15,000
6	12,200

Calculate the internal rate of return of the expansion, starting with a discount rate of 15%: 

a) 13%

b) 15.4%

c) 27.4%

d) 51.1%

9.4

Year	Cash flow	Discount factor at 15%	Present value at 15%	Discount factor at 16%	Present value at 16%
0	(50,000)	1.0000	(50,000)	1.0000	(50,000)
1	10,500	0.8696	9,131	0.8621	9,052
2	12,000	0.7561	9,073	0.7432	8,918
3	15,500	0.6575	10,191	0.6407	9,931
4	16,500	0.5718	9,435	0.5523	9,113
5	15,000	0.4972	7,458	0.4761	7,142
6	12,200	0.4323	5,274	0.4104	5,007
NPV			562		(837)

Note: When discounting at 15%, the NPV was positive. This means that the IRR required is greater than 15% and students should have selected a second discount rate greater than 15%.

Imag

A company is considering buying a new piece of equipment. The equipment will cost £55,000 and will be in use for 4 years. The equipment will be scrapped after this period.   

 

Excluding these amounts, the net cash flows for the equipment are as follows: 

Year	Cash flow £
1	17,500
2	15,000
3	20,000
4	25,000

 

Calculate the internal rate of return of the equipment, starting with a discount rate of 14%: 

a) 14.2%

b) 18.7%

c) 23%

d) 53.5%

9.4

Year	Cash flow	Discount factor at 14%	Present value at 14%	Discount factor at 15%	Present value at 15%
0	(55,000)	1.0000	(55,000)	1.0000	(55,000)
1	17,500	0.8772	15,351	0.8696	15,218
2	15,000	0.7695	11,543	0.7561	11,342
3	20,000	0.6750	13,500	0.6575	13,150
4	25,000	0.5921	14,803	0.5718	14,295
NPV			197		(995)

Image 4.6

Accessible text of image(opens in a new tab)

A company manufactures and sells woollen cloaks. It plans to invest in a modernised production line at a cost of £75,000. The production line has a 7-year useful life, at the end of which its scrap value is £10,500.  Excluding these amounts, the net cash flows arising from this investment will be as follows: 

Year	Annual cash flow £
1	20,000
2	19,000
3-5	19,500
6-7	13,000

Calculate the internal rate of return of the production line using appropriate discount rates: 

a) 15.4%

b) 17.2%

c) 22.8%

d) 24.2%

9.49.4

Year	Cash flow	Discount factor at 17%	Present value at 17%	Discount factor at 18%	Present value at 18%
0	(75,000)	1.0000	(75,000)	1.0000	(75,000)
1	20,000	0.8547	17,094	0.8475	16,950
2	19,000	0.7305	13,880	0.7182	13,646
3	19,500	0.6244	12,176	0.6086	11,868
4	19,500	0.5337	10,407	0.5158	10,058
5	19,500	0.4561	8,894	0.4371	8,523
6	13,000	0.3898	5,067	0.3704	4,815
7	23,500	0.3332	7,830	0.3139	7,377
NPV			348		(1,763)

Year 7 cash flow includes the scrap value of £10,500.

Note: You could have started with a different discount rate. The lowest multiple choice option is 15.4%, so 15% or 16% would also have been sensible starting points.

Image

9.4

Topic 2 - Discount rates to use for interpolation and extrapolation

Topic content

Topic 3 of 3

Advantages and disadvantages of IRR

Advantages of IRR

• •

  When considering one project with typical net cash flow patterns, the IRR technique will give the same conclusion as NPV, but the result is often more easily understood by non-accountants since it generates a relative measure.

• •

  The IRR technique gives due consideration to the time value of money.

Disadvantages of IRR

• •

  The calculation is more difficult to understand than other techniques such as ARR. 

• •

  If there are changes in the direction of cash flows over a project’s life (ie if there are negative net cash flows for a period), more than one IRR may be possible. 

• •

  Comparing IRRs for two projects of different sizes (ie different initial investments) may give different project ranking results compared to the NPV technique (the NPV technique should always be used where this conflict occurs).

Identify which of the following statements in relation to capital investment appraisal is/are TRUE: 

• a) When looking at more than one project, internal rate of return may give different project ranking results compared to net present value (NPV).  
  

• b) One of the advantages of the NPV technique is that it exactly measures the increase in shareholders’ wealth.
  

• c) If the accounting rate of return is calculated as being higher than a company’s weighted average cost of capital, the project should be accepted.  

9.4

The correct answers are a and b.

Companies set their target ARR subjectively so ARR cannot be compared meaningfully to the cost of capital.

A company has a budget of £275,000 to improve its production capacity.  The company’s production director has devised a number of proposals to do this, as follows:

Project	Cost of project £	NPV £
1	95,000	6,750
2	85,000	5,750
3	125,000	7,500
4	175,000	8,100
5	45,000	3,250

 

The projects are non-divisible.  

Calculate which combination of projects the company should undertake:  

a) 1 and 4

b) 1, 2 and 5

c) 1, 3 and 5

d) 3 and 4

9.5

The correct answer is c.

As projects are non-divisible, trial and error is required to find the optimal combination of projects. However, a quicker approach for this question is to calculate the return from each of the possible combinations of projects, ensuring that the total investment does not cost more than the £275,000 available.  

 

The returns for each combination are shown below: 

 

a) 1 and 4                  £14,850 

b) 1, 2 and 5             £15,750 

c) 1, 3 and 5             £17,500 

d) 3 and 4                 £15,600 

 

The highest overall NPV comes from option c and this combination requires a total investment of £265,000, which is within the £275,000 available.  

Note: Investing in both 3 and 4 will not be possible as this will exceed the available budget: £175,000 + £125,000 = £300,000.

A company is considering the following non-divisible projects but can only undertake two out of the four. Projects 1 and 3 require the same building and staff, so only one of these can be chosen, while projects 2 and 4 require the same site to be developed in different ways so cannot both be chosen.  

Project	Cost of project £	NPV £
1	600,000	65,000
2	800,000	29,000
3	400,000	68,000
4	280,000	30,000

Calculate the combination of projects the firm should undertake: 

a) 1 and 2

b) 1 and 4

c) 2 and 3

d) 3 and 4

9.5

The correct answer is d.

The returns for each combination are shown below: 

a) 1 and 2             £94,000 

b) 1 and 4             £95,000

c) 2 and 3             £97,000

d) 3 and 4             £98,000

Zeus plc (Zeus) has a capital budget of £220,000 for the coming year. A number of proposals for using this money are set out below: 

Project	Initial investment £	NPV £
A	80,000	8,000
B	40,000	32,000
C	100,000	60,000
D	60,000	30,000
E	120,000	84,000

 

Calculate which of them should be selected by Zeus, assuming that the projects are divisible: 

a) Projects A, B and C only

b) Projects D, E and two fifths of project C

c) Projects C, D and one half of project E

d) Projects B, E and three fifths of project C

9.5

The correct answer is d.

As the projects are divisible, the optimal combination can be selected by ranking projects according to their NPV per £1 of initial investment. 

Project	Initial outlay £	NPV of cash flows £	Benefit/ cost ratio	Ranking
A	80,000	8,000	0.1	5
B	40,000	32,000	0.8	1
C	100,000	60,000	0.6	3
D	60,000	30,000	0.5	4
E	120,000	84,000	0.7	2

On a divisible basis, the following would be selected: 

Project	Outlay £	NPV £
B	40,000	32,000
E	120,000	84,000
⅗ of project C	60,000	36,000
	220,000	152,000

Zeus plc (Zeus) has a capital budget of £220,000 for the coming year. A number of proposals for using this money are set out below: 

Project	Initial investment £	NPV £
A	80,000	8,000
B	40,000	32,000
C	100,000	60,000
D	60,000	30,000
E	120,000	84,000

 

Calculate which of them should be selected by Zeus, assuming that the projects are NOT divisible: 

a) Projects B, D and E

b) Projects A, C and E

c) Projects B, C and D

d) Projects A and E

9.5

The correct answer is a.

On a non-divisible basis, trial and error is required to select the optimal combination of projects.  

	Total investment £	Total NPV £
a) B, D and E	220,000	146,000
b) A, C and E	300,000	152,000
c) B, C and D	200,000	122,000
d) A and E	200,000	92,000

 

The highest NPV comes from undertaking projects A, C and E but this combination requires more than the £220,000 available for investment. The next highest NPV comes from B, D and E, which requires an investment possible from the available budget.