Cornell CS 2110 Flashcards

help me

static vs dynamically typed languages

static vs dynamically typed languages

Static typed languages require values to have specified types and functions to have return types to be declared before compilation (compile-time), while dynamically typed languages determine types during runtime.

final keyword

In programming, a final keyword used to declare constants that cannot be changed, classes that cannot be extended, or methods that cannot be overridden.

final int x = 5
//this x cannot be modified anymore
// x = 6 will give you an error

list the primitive types for prelim 1 (four) and define primitive types

boolean int double char

Primitive types are basic data types in programming that are not composed of other types and represent simple values directly.

references types

Reference types are data types in programming that store references to the memory location of an object rather than the actual data. Examples include classes, interfaces and arrays.

null

A term used to represent a missing or unknown value in a dataset, often denoted as "null" or "NaN" in programming languages.

casting (widening, casting an object’s static type to dynamic type)

we can assign new types of a value through widening

byte → short → int → long → float → double

so an int can be widened into a double, but a double cannot be widened into an int.

int num1 = 10;
double num2 = (double) num1;
System.out.println(num2); // Output: 10.0

• if you know an object’s dynami type, can cast an expression to recover access to additional behavior.

• however, if wrong, you will get a runtime error ClassCastException

King k = (King) p;

static methods

Static methods are functions in a class that can be called without creating an instance of the class. They are accessed using the class name.

Static type vs dynamic type

Static type: types declared for variables and return values (compile-time)

Dynamic type: the type of an object being referenced (runtime)

Dynamic Dispatch

The behavior (method) of an object is determined by the dynamic type. If the method exists in both the static type and dynamic type, then the object takes the behavior of the dynamic type.

class Piece(){
   ....
   void legalMove(){ 
       ....
   }
}

class King() extends Piece{
  ...
  @Override
  void legalMove(){ //some code
  }
  void canCastle(){...}
}

Piece p = new King();
p.legalMove(); //will take the method legalMove from KING, not Piece

Compile-time reference rule

client can only request behavior supported by the target’s static type

class Piece(){
   ....
   void legalMove(){ 
       ....
   }
}

class King() extends Piece{
  ...
  @Override
  void legalMove(){ //some code
  }
  void canCastle(){...}
}

Piece p = new King();
p.canCastle() //GIVE AN ERROR because canCastle does not exist in class Piece. 

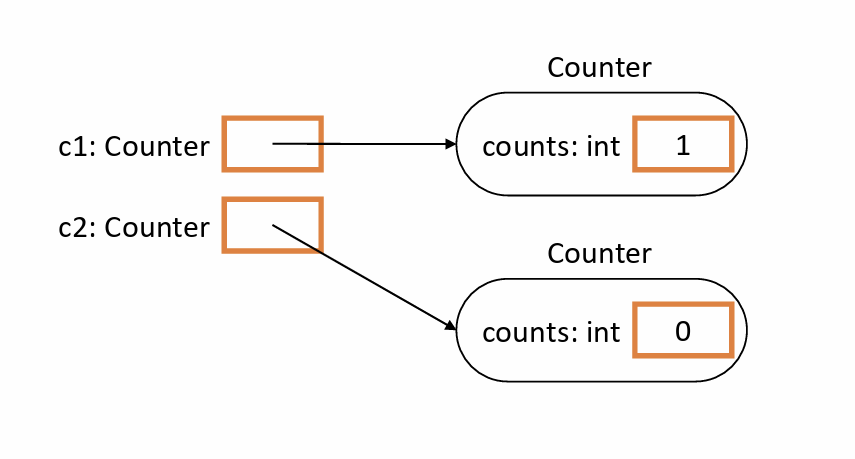
Object Mapping Diagram for this Counter class (Lec 2)

image

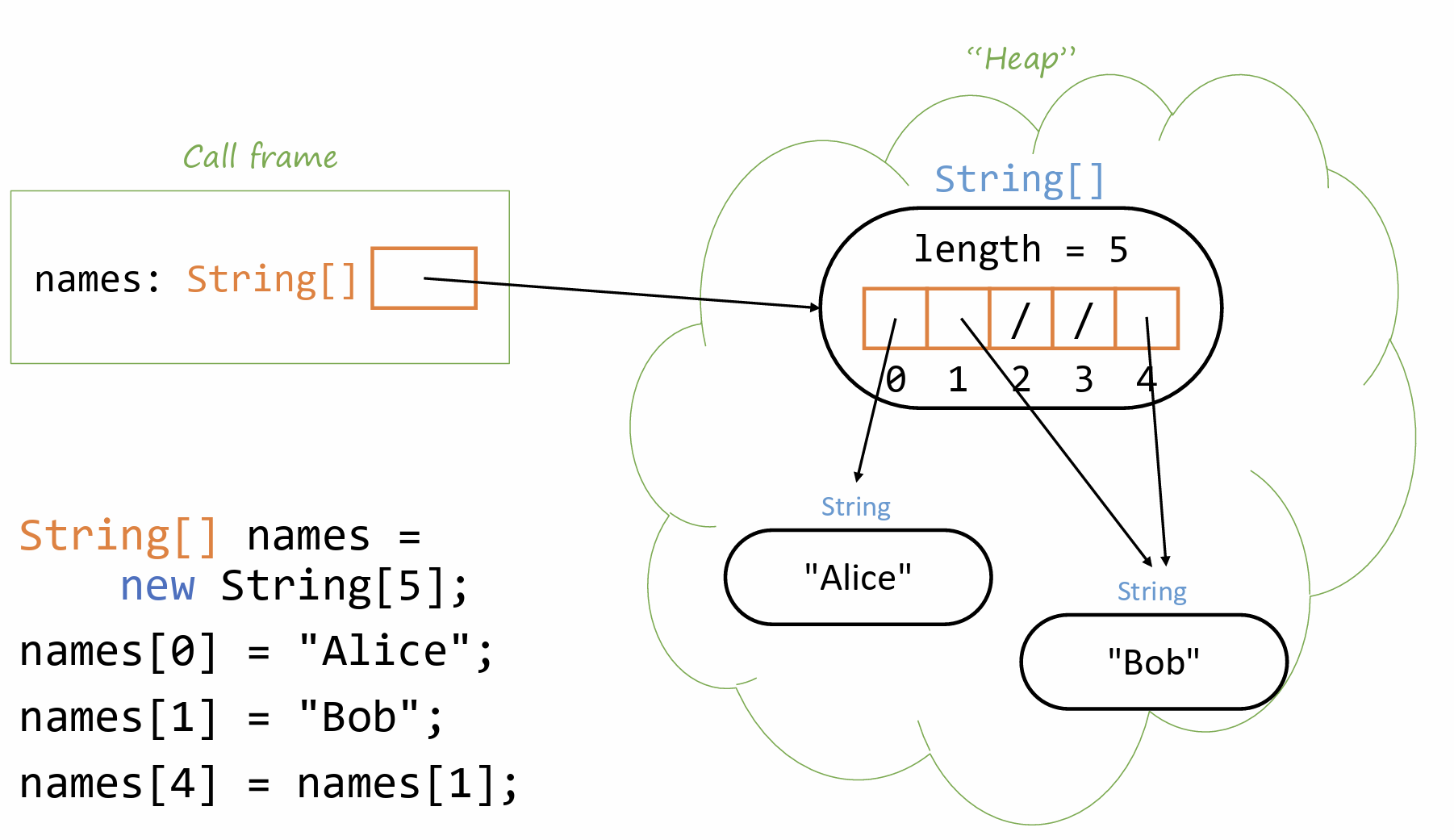
Object Mapping Diagram for arrays (Lec 3)

image

wrapper classes and autoboxing

Wrapper classes are classes that allow primitive data types to be used as objects. Autoboxing is the automatic conversion of primitive data types to their corresponding wrapper class objects.

For example, int → Integer

practice writing code for Exception

1. try/catch statement

2. check vs unchecked exceptions

3. throw and throws clause

try/catch:

• respond to a problem

try{
  //some sick code
}catch (Exception_name e){
 System.out.println("Exception caught");
}

throws clause

• disclose that problems MIGHT arise

• goes in method declarations

• is not needed when we have a try catch block (prelim 1 misconceptions)

public String readString() throws IOException

throw statement:

• report a problem

throw new IOException();

checked exceptions must be handled, while unchcked exceptions don’t have to be

Checked exceptions are required to be handled by the code, while unchecked exceptions do not need to be handled. Checked exceptions are checked at compile time.

class invariants

Class invariants are conditions that must always be true for an object of a class. They help ensure the integrity of the object's data and behavior.

• truthfulness not affected by methods

preconditions vs postconditions

Preconditions: Specify conditions that must be true at the start of a method.

Postconditions: Specify conditions that must be true at the end of a method.

method specifications

Method specifications in Java are a set of rules that define the behavior and requirements of a method, including parameters, return type, and exceptions.

immutable vs mutable (vs final variable)

immutable types cannot change their state

mutable types can change their state

a final variable can only be assigned to once.

final int serialNum = sn;
serialNum = 2; //not allowed

note that variables change value through assignment, so you can re-assign immutable types.

abstraction: client vs implementer roles

implementer:

• must maintain class invariant

• provide correct behavior

• may use defensive programming

• follow postconditions

• returns, modifies/effects

client:

• should be able to use class for any purpose and never get incorrect behavior.

• follow preconditions

• requires

notice how CLASS INVARIANTS ARE ALWAYS TRUE

encapsulation

The concept of bundling data and methods within a class, where the data is hidden from outside access and can only be modified through the class's methods. only class implementer can access 100% of the data within the class.

• create an abstraction barrier

public, private, protected modifiers

public: anyone can access fields / invoke methods

private: only the clss implemeentation can access fields/ invoke methods

protected : allows a class to restrict access to its fields, methods, and constructors within the same package or by any subclass of that class, regardless of the package.

black box testing vs glass box testing

black box testing:

• verify method postconditions against their pec, BUT WE DON’T KNOW THE METHOD IMPLEMENTATION

glass box testing:

• LOOK AT IMPLEMENTATION!

• can measure it through “line coverage”

• disadvantage: breaks abstraction barrier

interfaces (def, subtype relationship)

• guarantee to clients what a type CAN DO, without committing to details.

  • method signatures

  • method return types

  • method specs

• method declarations are implicitly public

subtype:

• implementing an interface establishes a subtype relationship

• TwoPtInterval <: Interval

• CenterINterval <: Interval

Object Diagram practice:

umm sory just go on lecture

instanceof vs getClass()

expr instanceof T is true if the dynamic type of expr is a subtype of T.]

get cl

Array bag (fixed capacity)

runtime for add() and frequencyOf() ?

add(): independent of size O(1)

frequencyOf(): dependent of size O(n)

Linked Bag (unbounded capacity)

add()

frequencyOf()

add(): worse case dependent, best case independent O(n)

frequencyOf(): always dependent O(n)

Linked List

addAt()

hasDuplicates()

addAt(): best case independent, worse case dependent O(n)

hasDuplicates: not only dependent, but much slower O(n²)

subclasses

subclasses allow a derived class to inherit fields and method bodies from a parent class.

class Derived extends Parent {...}

Type Hierarchy for Exceptions

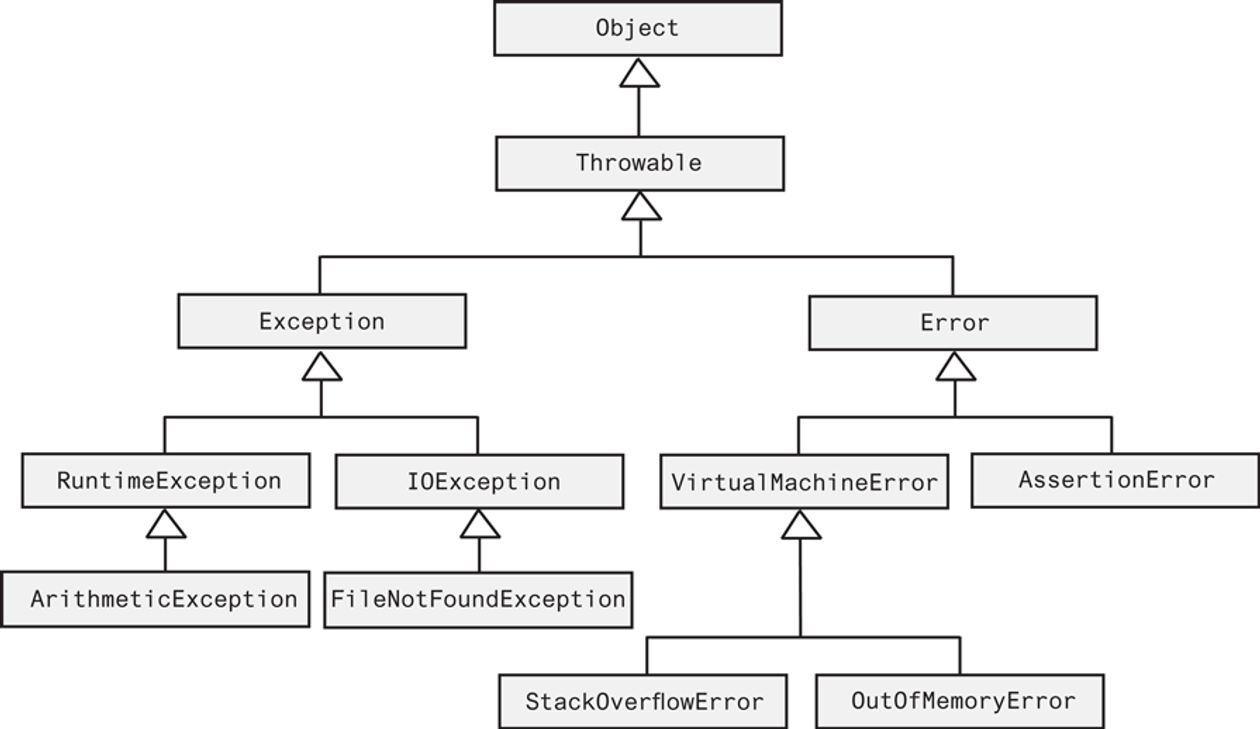
Bags (simple definition, at least four operations)

• finite collection of objects in no particular order

1. size(): in

2. empty(): boolean

3. add(newItem)

4. remove(anItem)

5. contains(anItem): boolean

6. frequencyOf(anItem)

Generic Types/parametric polymorphism

classes and interfaces can be parameterized on a generic type

interface Bag<T> {}

class ArrayBag<T> implements Bag<T>{}

efficiency of ArrayBag, Resizable ArrayBag and LinkedBag for add() and frequency Of()

• in terms of items in ba

ArrayBag:

• add(): independent of size;

• frequencyOf(): dependent on size

Resizable Array Bag:

• add(): sometimes dependent of size (APPEND)

• frequencyOf(): dependent on size

LinkedBag:

• add(): independent of size (PREPEND)

• frequencyOf(): dependent on size

efficiency of LinkedList.addAt()

best case

worst case

best case: insert at head or tail. independent of size of list

worst case: insert at middle and even worse: insert right before tail; dependent on the size of list

Match the big Oh notation to the vocab word

O(1),

O(logn)

O(n)

O(n²)

O(2^n)

constant, logarithmic, linear, quadratic, exponential

What are the efficiencies of these methods in Big O Notation?

Yeah slayyyyy

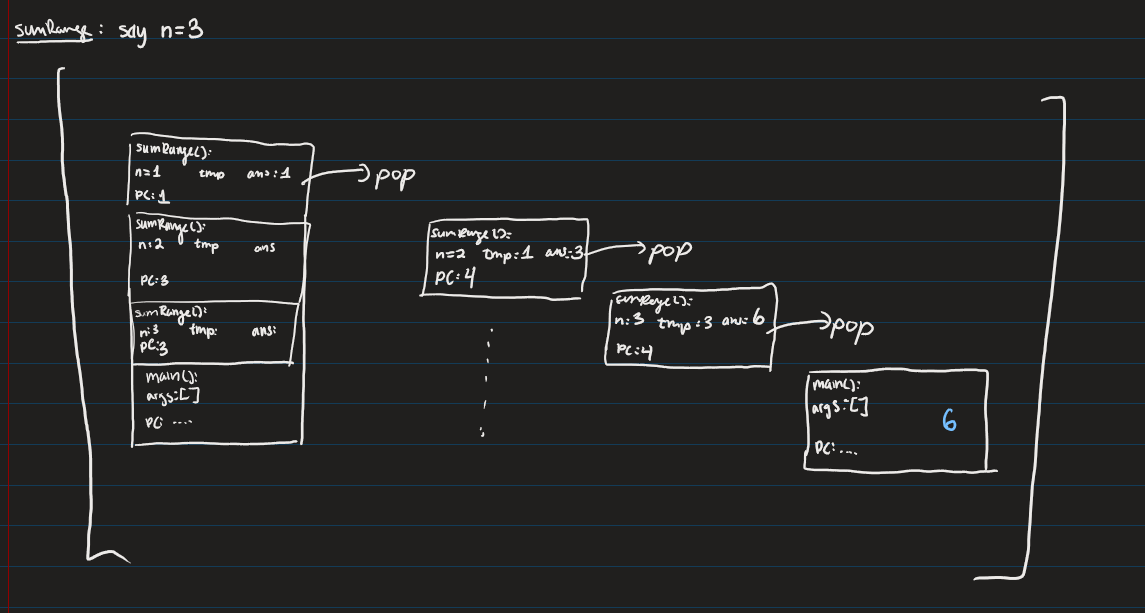
Recursive Call Stack Object Diagram notatioin, what should the elements be made of

A function’s parameters

• A function’s local variables • The instruction the function is currently executing

• PC: “Program Counter

Recursive Call Stack Object Diagram Example:

t

img

final answer is 6

Time complexity and space complexity for recursion

Time complexity: proportional to the # of recursive calls

Space complexity: proportional to max depth. of the call stack (can be less than the # of recursive calls)

turning a static recursive function into an instance recursive method

usually instead of calling fields, or the class name (so like ClassName.methodName) , we can just use this

Recursion with quotient remainder thingy

for example:

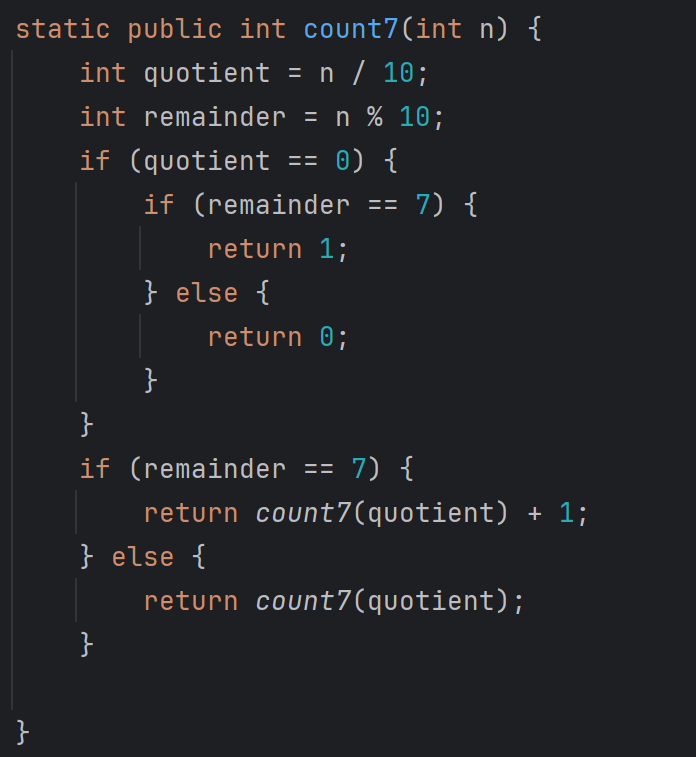
• Implement a specified function using recursion. The problem to be solved can be broken into identical but smaller problems. Example: determine the number of ‘7’ digits in a number’s decimal form, leveraging the quotient and remainder when the number is divided by 10.

• so `1456787` the answer will be 2, because there are two ‘7’ digits.

my ans for it

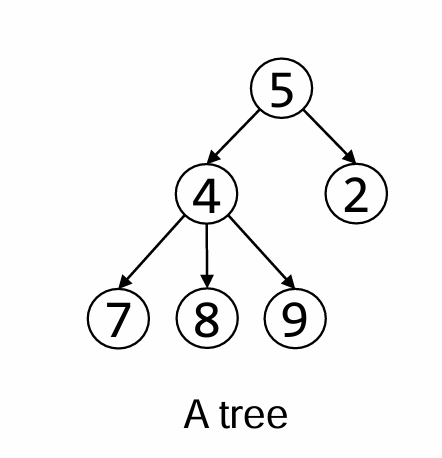
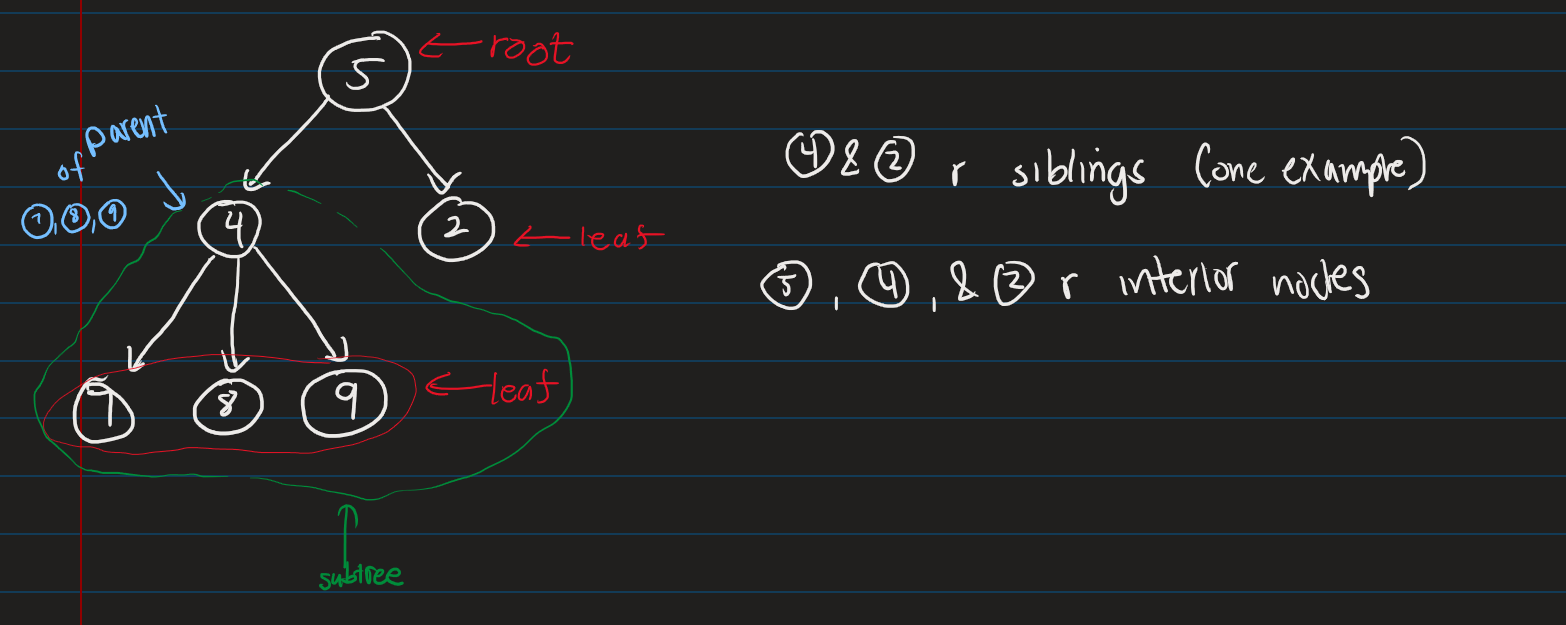
Tree terminology:

• Given a diagram of a tree, circle examples of the following: leaf, parent and child, subtree, root, interior node, siblings and descendants and ancestors of a given node.

• What is the height and width of the tree in the image?

• What is the time and space complexity of size() and height()? (not in terms of n, but in terms of size and height)

height max at 2 (0-based), depth is 3 (1-based)

size is 6

so in really simple terms it would be O(n) but usually isn’t good enough

time complexity:

• size(): O(size)

• height(): O(size)

space complexity:

• size(): O(height)

• height(): O(height)

General Tree vs Binary Tree

General Tree: Each node may have any number of children; might not be ordered

Binary Tree: Each node has at most 2 children, distinguished as “left” and “right

Binary Search Tree (BST), what is the BST invariant (so what defines the BST)

Which of the following is not a BSTs?

1. All values in left subtree are less than this node’s value

2. All values in right subtree are greater than this node’s value

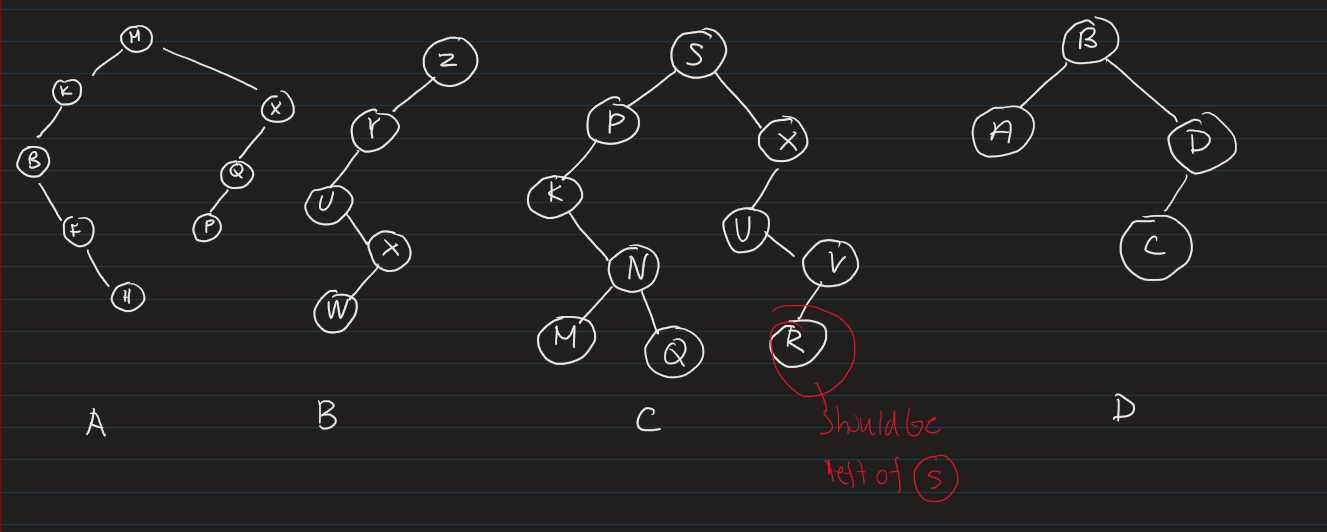
Code snippets:

Given a declaration of a tree node class for a general tree, how would one create a recursive function to find

1. size()

2. height()

3. height the depth of a node containing a given value.

1. the return function would be something along the lines of

   return left.size() + right.size() + 1;

   for the base case, if the curr node is null (or something along those lines in OOP), then you return 0

   here is the iterative code from the lecture

       /**
        * Return the number of nodes in the tree rooted at this node.
        */
       int size() {
           int nodeCount = 1;
           for (TreeNode<T> child : children) {
               nodeCount += child.size();
           }
           return nodeCount;
       }
   

   here is the recursive code from the lecture (although for BST… can work on a normal tree too)

       /**
        * Return the number of nodes in the tree rooted at this node.
        */
       int size() {
           int leftSize = (left == null) ? 0 : left.size();
           int rightSize = (right == null) ? 0 : right.size();
           return 1 + leftSize + rightSize;
       }

2. the return function would be something along the lines of

   max(left.height(), right.height()) + 1

   for the base case, if the curr node is null (or something along those lines in OOP), then you return 0

   here is the iterative code from the lecture

       /**
        * Return the number of nodes in the longest path from this node to a leaf.  The height of a
        * leaf is 1.
        */
       int height() {
           int maxChildHeight = 0;
           for (TreeNode<T> child : children) {
               maxChildHeight = Math.max(maxChildHeight, child.height());
           }
           return 1 + maxChildHeight;
       }

   here is the recursive code from the lecture (for BST, but prob. work for binary tree, too)

       /**
        * Return the number of nodes in the longest path from this node to a leaf.  The height of a
        * leaf is 1.
        */
       int height() {
           int leftHeight = (left == null) ? 0 : left.height();
           int rightHeight = (right == null) ? 0 : right.height();
           return 1 + Math.max(leftHeight, rightHeight);
       }

3. Basically we have to go through ALL NODES of the tree (similar traversal as size()), but we some sort of condition that we have to succeed in order to increment our count.

   Here is the code from this tree3binary.pdf (cornell.edu)

   /** = number of nodes of t that contain v. 
   * Note: t can be null. */ 
   public int ct(TreeNode t, T v) { 
   } 
   if (t == null) return 0; 
   int c=  v.equals(t.data) ? 1 : 0; 
   return c + ct(t.left, v) + ct(t.right, v);

Code snippets:

• Given the declaration of a BST node class, implement a recursive or iterative method for a specified operation. The operation might be familiar from the textbook or lecture, or it might be new.

• contains(), add(), find minimun value in tree, find max. value in tree

• for now this are all instance() methods (not static… can do static but im not putting the answers down here)

Can declare a charBST, subtype comparable BST, or comparator BST.

charBST

• contains()

      // Instance method
      /**
       * Return whether the tree rooted at this node contains the value `target`.
       */
      boolean contains(char target) {
          if (data == target) {
              return true;
          }
          if (target < data) {
              return (left == null) ? false : left.contains(target);
          } else {
              return (right == null) ? false : right.contains(target);
          }
      }
  

• add()

  has a special precondition…sometimes can add

      /**
       * Insert value `c` into the tree rooted at this node.  Requires `c` is not contained in the
       * tree.
       */
      void insert(char c) {
          // TODO: relax precondition
          assert c != data;
  
          if (c < data) {
              if (left == null) {
                  left = new BstCharNode(c);
              } else {
                  left.insert(c);
              }
          } else {
              if (right == null) {
                  right = new BstCharNode(c);
              } else {
                  right.insert(c);
              }
          }
      }
  

• find smallest value

  i think will be something like this

  char min(){
     if(left == null) return data; //this is the smallest value
     return left.min(); 
  }

• find biggest value

  char max(){
    if (right == null) return data;
    return right.max();
  }
  

BST with subtype Comparable

for the following functions, they are basically the same, but instead of using ==, <, and >, we have to use a.compareTo(b) == 0, > 0, < 0 instead.

we can also use a.equals(b)

How to write the class that uses subtype Comparable (i.e: String and Trees)

How to write an instance using lambda expression that uses Comparator

class String implements Comparable

class BSTComparableNode<T extends Comparable<T>>

create an instance of something, and the parameter will have one argument, the interface Comparable, where the method compareTo is defined.

example lambda expression:

• note that compareTo is from Comparable, since netid() returns a String,which implements Comparable.

 (a, b) -> {
 return a.netid().compareTo(b.netid());
 })

without lambda expression example:

new Comparator<T>() { //T will be replaced with something specific, like maybe a Student, or Point class. 
                @Override
                public int compare(T e1,
                       T e2) { 
                    return e1.getValue().compareTo(e2.getValue());
                }
            });

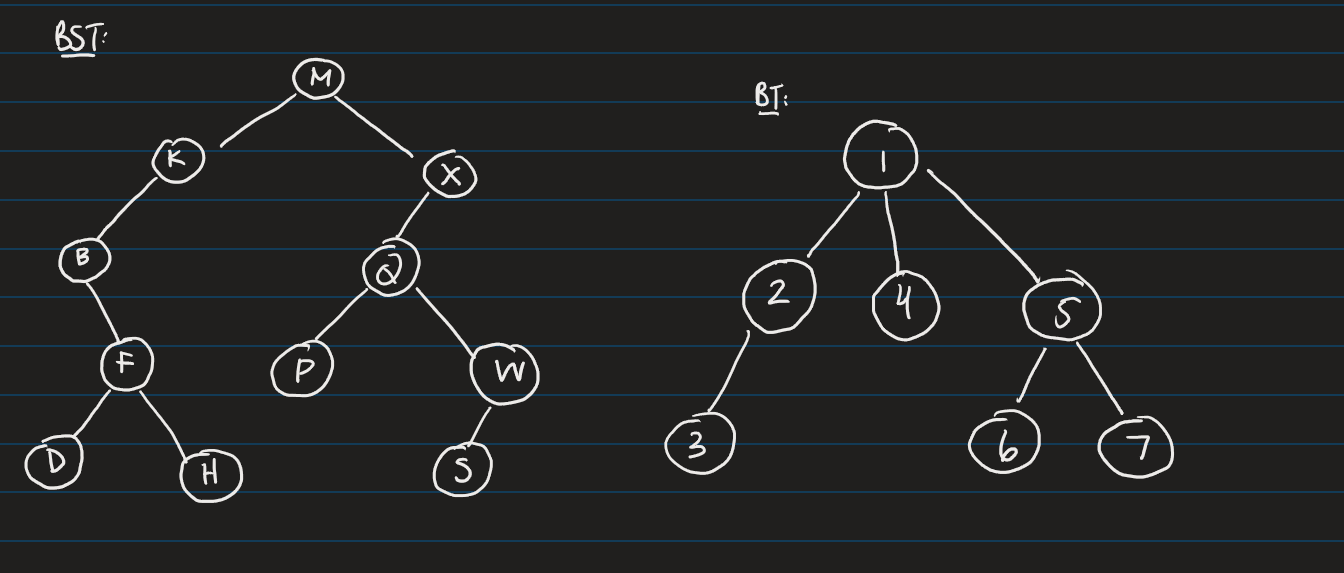
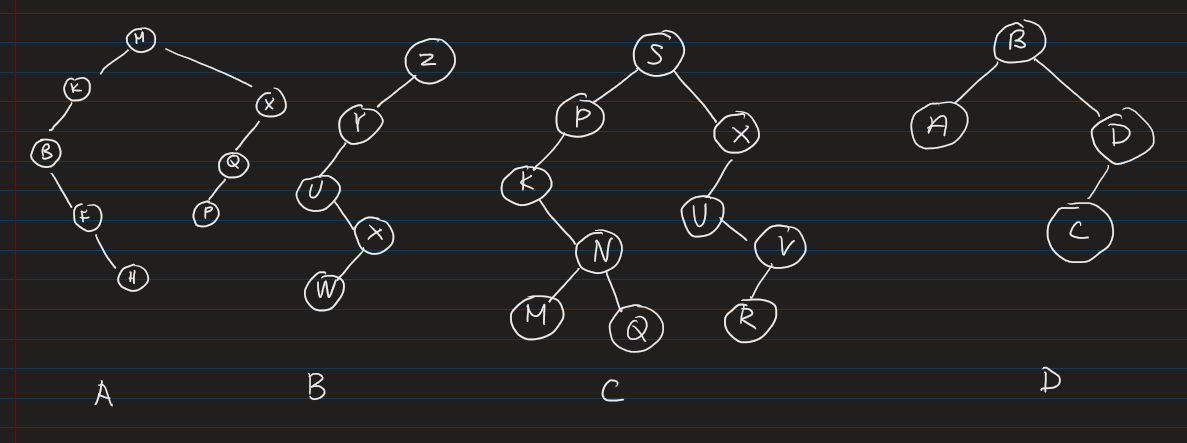
What is preorder, postorder of the given binary tree, and inorder traversal of the given BST.

PreOrder:

1. Visit self

2. Traverse left subtree

3. Traverse right subtree

   ANS: M, K, B, F, D, H, X, Q, P, W, S.

General trees

1. Visit self

2. Traverse child subtrees (in order)

   Ans: 1,2,3,4,5,6,7

Postorder:

1. Traverse left subtree

2. Traverse right subtree

3. Visit self

   Ans: D, H, F, B, K, P, S, W, Q, X, M

General Tree

1. Traverse child subtrees (in order)

2. Visit self

   Ans: 3, 2, 4, 6, 7, 5, 1

Inorder Traversal:

1. Traverse left subtree

2. Visit self

3. Traverse right subtree

   Ans: B, D, F, H, K, M, P, Q, S, W, X

Look CheckList/Four Loopy Questions

What does each question mean?

1. Does it start right? (establishment/initialization)

   Loop invariant must be true just before while • Aka establishment or initialization

   Accomplished by assigning to loop variables to truthify invariant

2. Does it maintain the invariant? (preservation)

   Body must maintain invariant: • Invariant must be true after body

   In reasoning about that, we get to assume that invariant is true before body • We also get to assume guard holds before body executes (“precondition” of loop body)

3. Does it end right? (postcondition)

   Loop invariant must be true just after while

   And postcondition must be met when loop invariant is true guard just became false

4. (Does it make progress?) (termination)

   Body must make progress toward termination

   ususally by decreasing something to zero, to where guard becomes false. this is called the decrementing function.

Loop Invariant

1. Definition

2. When it should hold true (i.e: While loop)

3. Explain the loop invariant of the given example

Defintion:

A specification. Just as functions need them, so do loops. It’s a comment that describes what is always true before and after loop body.

WHen hold true: check image

Loop Invariant:

something along the lines of, // inv: count is freq of item in first i elements of items

Explain linear search algorithm

1. What is the invariant?

v is not in [0,i). v is in [i..]

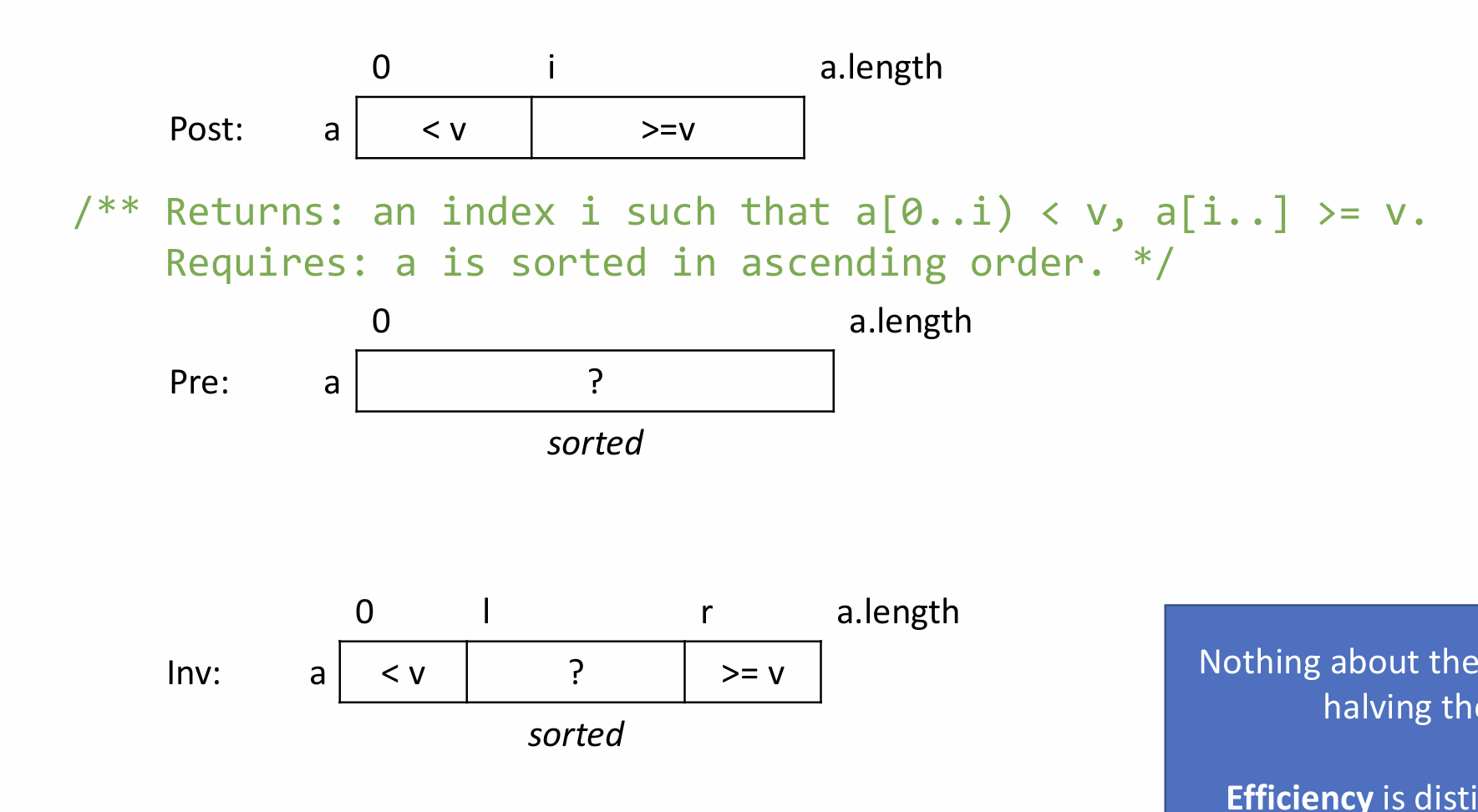
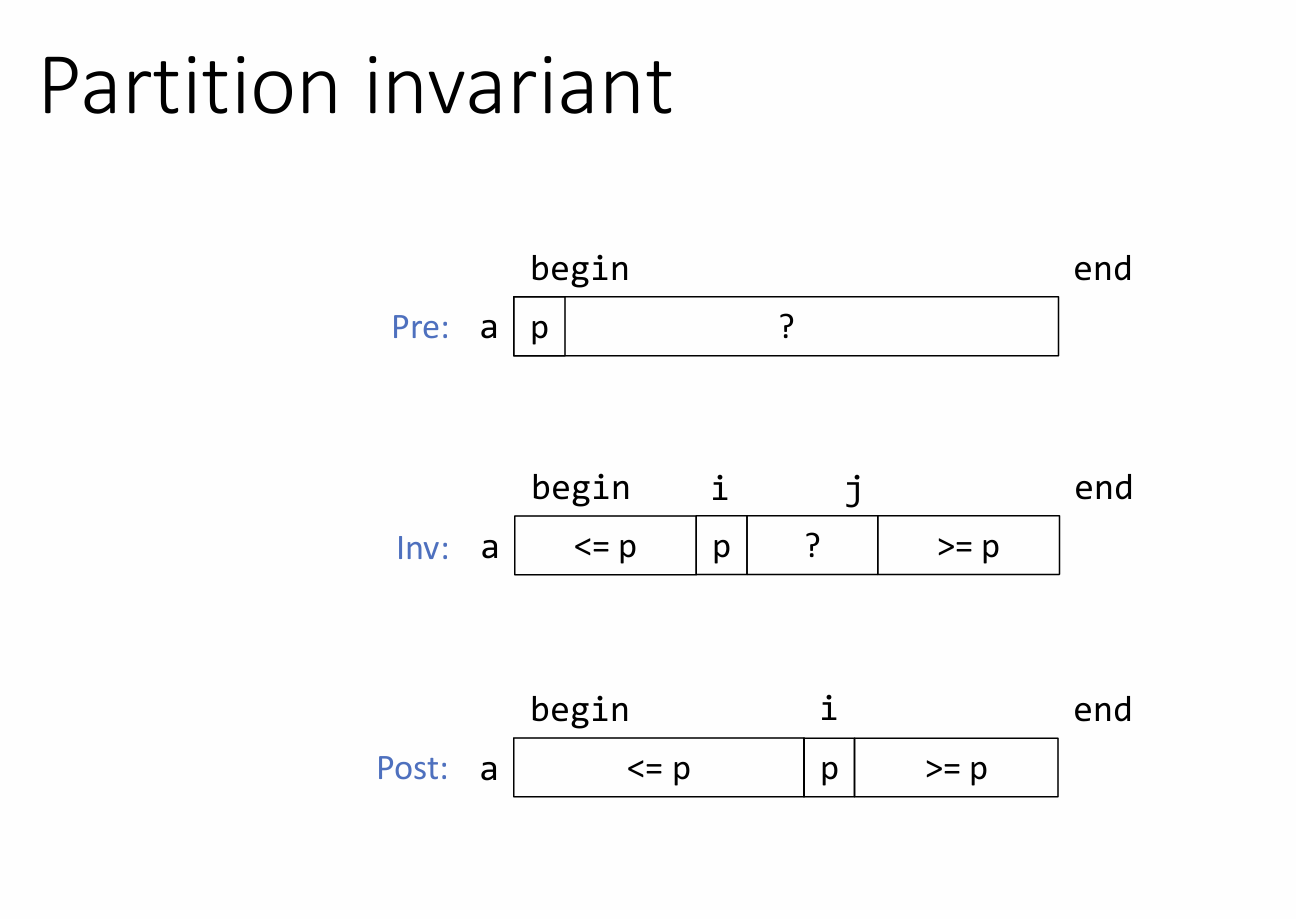
Explain binary search algorithm

Write the post, pre, and invariant in the array notation

image

so for the pre, seems like the array is just all unknown (unless there is some precondition using the variables, but in case all we know its sorted). for the invariant, some part is still unknown because we aren’t done.

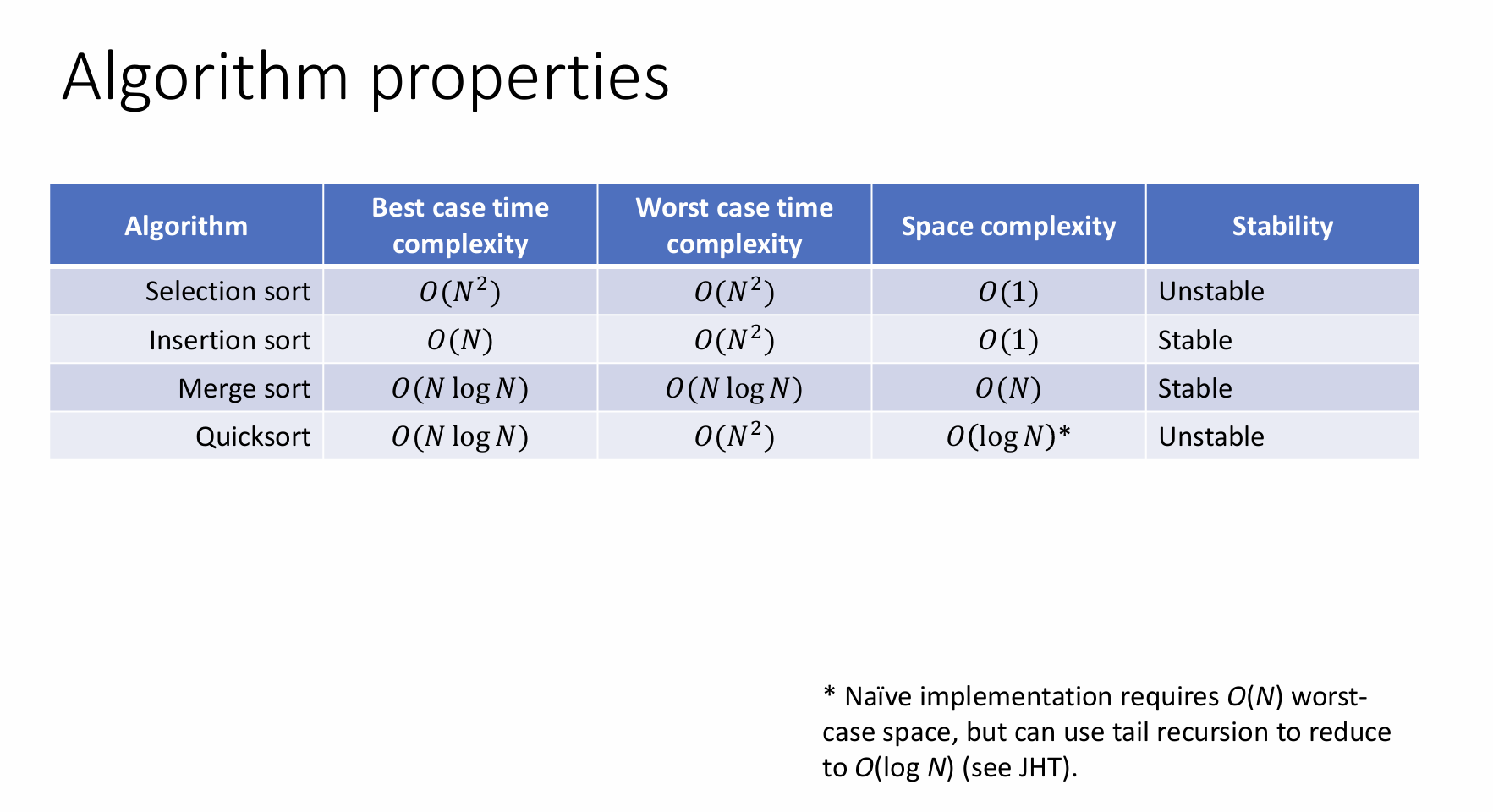
Among selection sort, insertion sort, merge sort, and quicksort, identify which algorithms are stable, and explain why.

Stable: insertion sort, merge sort

Unstable: selection sort, quicksort

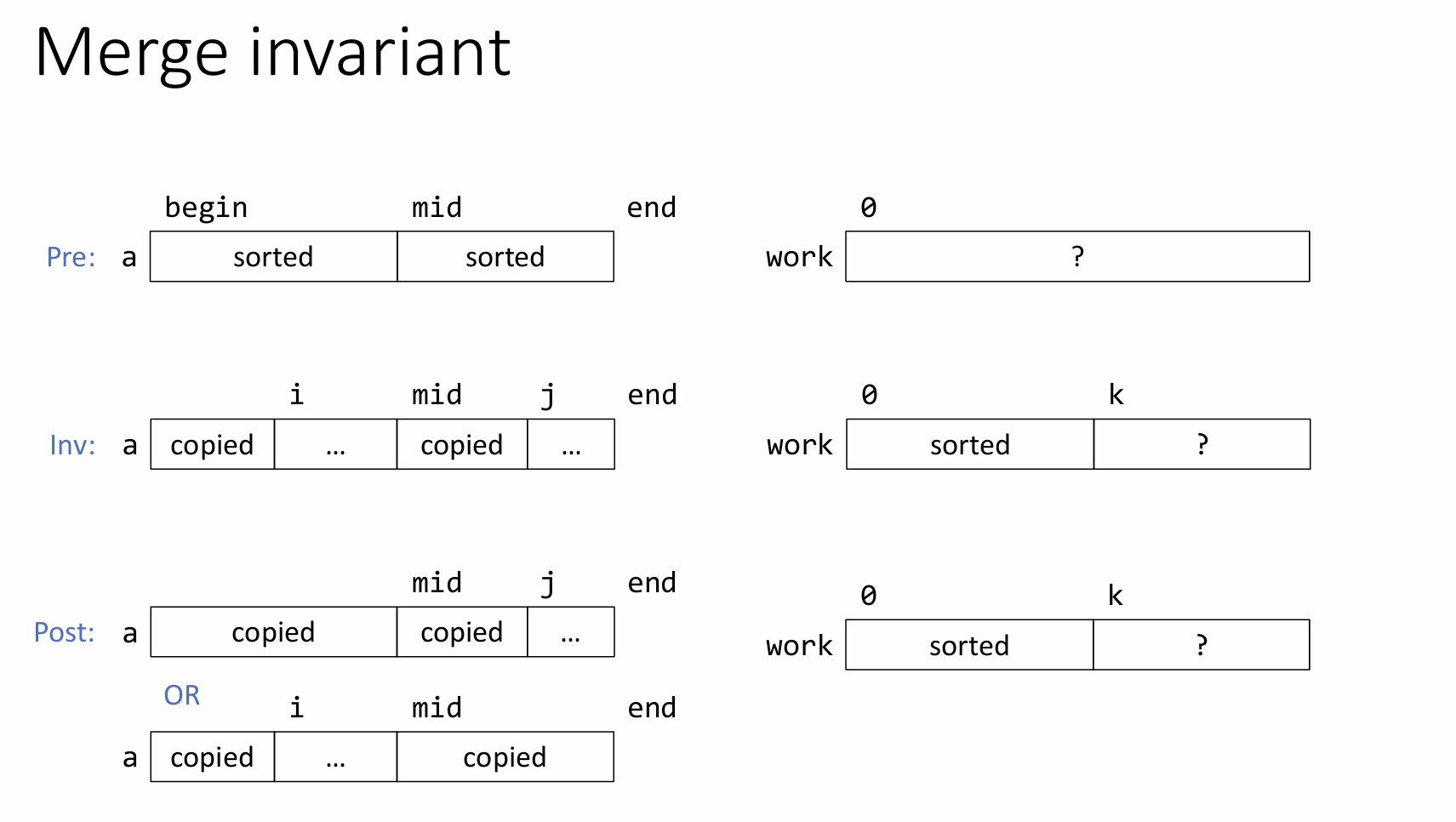
what is mergesort (stable, unstable), what is the loop invariant?

in english words: so usually theres like two functions

1. Sort left half of array (using merge sort)

2. Sort right half of array (using merge sort)

3. Mergeleft and right subarrays

This is recursive, until merge into the array with the same size of the original array.

loop invariant for the function merge, not mergeSort: image

stable: since when there’s duplicate elements, the most left one is picked as the ‘smaller’ one in the output ordering.

what is quicksort (stable, unstable), what is the loop invariant?

In english:

1. Partition array about a “pivot”

2. Sort the subarray of values less than the pivot

3. Sort the subarray of values greater than the pivot'

loop invariant: image (not that there is now i and j, so important distinction)

unstable: During this partitioning step, elements that compare as equal may be swapped, potentially altering their order from the original array.

(this card doesn’t actually have answers. just to let you know that the other flashcards on each sorting method has this information)

Given a loop invariant in array range or array diagram notation, state whether it is consistent with the outer loop of selection sort, the outer loop of insertion sort, an insertion procedure for insertion sort, or a partitioning algorithm for quicksort.

n/a

what is insertion sort (stable, unstable?), what is the loop invariant(s)?

in english words: 1. Move next unsorted into sorted position

in more mathy words:

elements from [0,i) are sorted.

pick element a[i], and go through [0,i) and insert it in the proper order

loop invariant: image

stable: because elements only move right-to-left and stop when they hit a duplicate

what is selection sort (stable, unstable?), what is the loop invariant(s)?

in english words: 1. Find smallest unsorted 2. Swap with first unsorted

in more mathy words:

Elements left of i (exclusive) are sorted. elements right of i (inclusive) are in unsorted order.

pick the smallest element to the right of i (inclusive), swap the position of that smallest element and a[i].

loop invariants: (image)

why is it unstable?

• swapping cant preserver ordering when there are duplicates(so differet names, but same years, the input ordering may not be the same as the output ordering)

• State the best-case time complexity for insertion sort and quicksort and describe the conditions in which it is achieved.

• State the worst-case time complexity for selection sort, insertion sort, merge sort, and quicksort.

• State the best-case space complexity for selection sort, insertion sort, merge sort, and quicksort.

  
  (just memorize at this point)

Image

Implement selection sort, insertion sort, and a partition procedure for quicksort, given relevant loop invariants. Values may be primitive types or subtypes of Comparable, or a Comparator may be provided.

selection sort invariant:

• outer loop: a[0, i) is sorted, a[i…] >= a[0..i)

• inner loop: (i made this myself) //invariant: a[jSmallest] <= a[i..]

insertion sort invariant:

• outer loop: Invariant: a[0..i) is sorted, a[i..] is unchanged

• inner loop: Invariant: a[j] < a[j+1..i]

quicksort partition procedure invariant:

/**
     * Partition `a[begin..end)` about a selected pivot `a[i]` such that `a[begin..i) <= a[i]` and
     * `a[i+1..end) >= a[i]` (as determined by `cmp`), returning `i`.  Requires `end > begin`.
     */

check quicksort for how to use cmp 🙂

Selection sort:

 // Invariant: a[0..i) is sorted, a[i..] >= a[0..i)
 int i = 0;
 while (i < a.length- 1) { // (i < a.length) works too

   // Find index of smallest element in a[i..]
   int jSmallest = i;
   //invariant: a[jSmallest] <= a[i..]
   for (int j = i + 1; j < a.length; ++j) {
        if (a[j] < a[jSmallest]) {
           jSmallest = j;
       }
   }
 
   // Swap smallest element to extend sorted portion
   swap(a, i, jSmallest);
   i += 1;
 }

Insertion sort:

int i = 0;
// Invariant: a[0..i) is sorted, a[i..] is unchanged
while( i < a.length) {
   int j = i;
   // Invariant: a[j] < a[j+1..i]
   while( j > 0 && a[j-1] > a[j]){
       swap(a, j-1, j);]
       j-=1;
   }
   i++;
}

Partition Procedure for quicksort:

 /**
     * Partition `a[begin..end)` about a selected pivot `a[i]` such that `a[begin..i) <= a[i]` and
     * `a[i+1..end) >= a[i]` (as determined by `cmp`), returning `i`.  Requires `end > begin`.
     */
    static <T> int partition(T[] a, int begin, int end, Comparator<T> cmp) {
        // Choose pivot and swap to beginning of array view
        int iPivot = begin;  // FIXME: bad choice - leads to worst-case behavior for sorted input
        swap(a, begin, iPivot);

        // Invariant: a[begin..i) <= a[i], a(j..end) >= a[i]
        int i = begin;
        int j = end - 1;
        while (i < j) {
            // FIXME: pivot will be first among duplicates - leads to worst-base behavior for
            // duplicated input.
            if (cmp.compare(a[i], a[i + 1]) > 0) {
                swap(a, i, i + 1);
                i += 1;
            } else {
                swap(a, i + 1, j);
                j -= 1;
            }
        }
        return i;
    }

Implement merge sort and quicksort, given the specifications for “merge” and “partition” methods (which you do not need to implement).

mergesort:

    /**
     * Sort `a[begin..end)` in ascending order (as determined by `cmp`).  Will overwrite values in
     * scratch array `work`.  Scratch array must be at least as long as the view being sorted.
     */
    static <T> void mergeSort(T[] a, int begin, int end, Comparator<T> cmp, T[] work) {
        // Base case: an array of 0 or 1 element is already sorted
        if (end - begin <= 1) {
            return;
        }

        int mid = begin + (end - begin) / 2;
        mergeSort(a, begin, mid, cmp, work);
        mergeSort(a, mid, end, cmp, work);
        merge(a, begin, mid, end, cmp, work);
    }

quicksort:

• NVM I GUESS WE NEED TO KNOW TAIL RECURSION

/**
     * Sort `a[begin..end)` in ascending order (as determined by `cmp`).
     */
    static <T> void quickSort(T[] a, int begin, int end, Comparator<T> cmp) {
        // Fully recursive
        // Base case: an array of 0 or 1 element is already sorted
        if (end - begin <= 1) {
            return;
        }

        int iPivot = partition(a, begin, end, cmp);
        quickSort(a, begin, iPivot, cmp);
        quickSort(a, iPivot + 1, end, cmp);

        // Tail recursion optimized
        /*
        while (end - begin > 1) {
            int iPivot = partition(a, begin, end, cmp);
            if (iPivot - begin < end - iPivot + 1) {
                quickSort(a, begin, iPivot, cmp);
                begin = iPivot + 1;
            } else {
                quickSort(a, iPivot + 1, end, cmp);
                end = iPivot;
            }
        }
        */
    }

Given an “entry” class, implement a dictionary’s “put” and “get” operations using a binary search tree data structure.

Lecture: Dictionary & Hashing

• Um hopefully this is just a binary sesarch tree add() and get() that another flashcard talked about.

State the worst-case time complexity of a dictionary’s “put” and “get” operations if entries are stored in a sorted or unsorted list.

Lecture: Dictionary & Hashing

Unsorted List:

put: O(1)

get: O(n)

Sorted List:

put: O(n)

get: O(log n)

Evaluate a proposed hashCode() method in terms of collision avoidance and consistency with equals().

Two step process:

1. Hash a key into an int (“hash code”)

2. Turn a hash code into an array index (“index derivation”)

• Depends on array length!

We can use the Object method hashCode() in order to do this. We have to make sure that we pick a good mthod so that the function returns values distributed over the ENTIRE range of ints, eve for inputs that seem very similar, so we can avoid as many collisions as possible.

An implementer must ensure hash code is consistent with equality

• If overriding equals(), must override hashCode() too!

Goal: two non-equal objects should be unlikely to share a hash code (unlikely to have a collision)

• Should depend on all of an object’s state

• Should depend on ordering of any sequential state (e.g. arrays)

• Should span whole range of integers

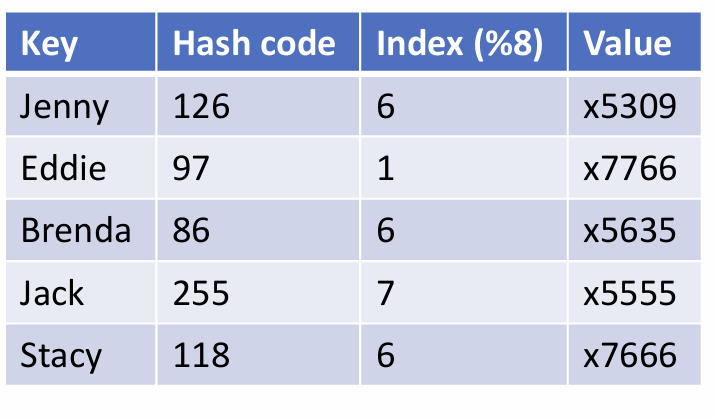
Given a key’s hash code and the length of a hash table array, state which element of the array the key should be stored under if indices are derived by taking the positive remainder mod the table length.

Let say h(“Hopper”) -> -95141326;

The size of the array is 8.

index in the hash table should be

abs(-95141326 % a.length)

(-95141326 % 8 ) = 6

should be in index 6

Linear probing vs Chaining

best and worse time complexity for chaining

Chaining:

• Treat array elements as “buckets” storing a collection of entries (e.g. a linked list)

• Finding the right bucket is O(1), but searching it will be slower

• Best: O(1): .hashCode() is O(1), derive index: O(1), value is empty, so just put it in O(1).

• Worse: collisions every where, and there are n elements already in the bucket. O(n).

Linear Probing:

• Array elements point directly to entries

• If desired element is occupied, pick the next element to try according to a probing sequence

Given a key’s hash code and the contents of a hash table array, state which element an entry with that key would be stored in if linear probing is used to resolve collisions.

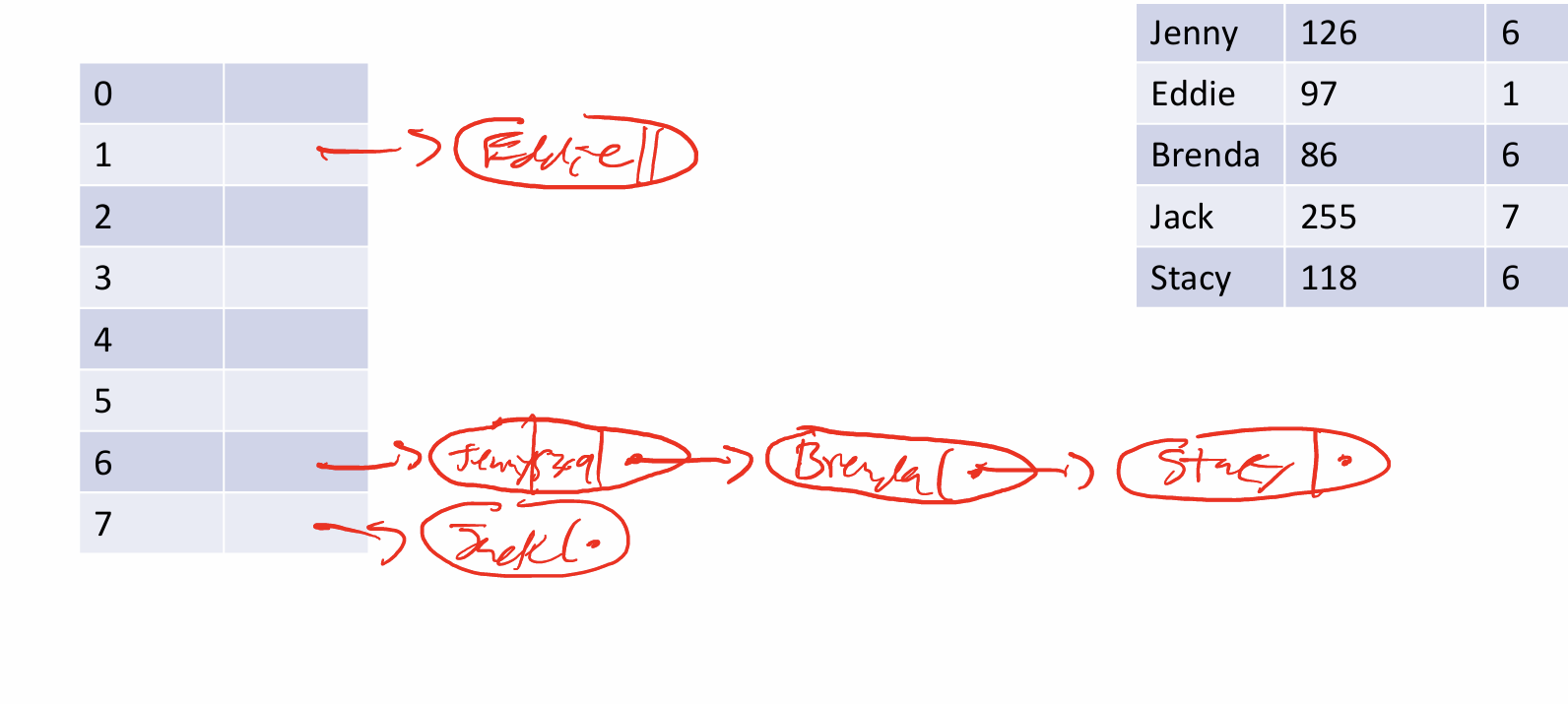
Given the contents of the buckets of a hash table using chaining and the hash codes of all keys stored in it, draw the table and its buckets’ contents after the table is resized to a given new size, assuming indices are derived by taking the positive remainder mod the table length.

ans: image

ans2: just redo the whole thing, just mod but the new array length!!!!!

What is load factor!

What is the cost of lookup with chaining

What is lambda when array size is fixed?

what is lambda wen array size is proportional to N, the number of elements?

What is the cost of resizing array of N, what is the cost of amortized cost of resizing array of N?

lambda = #of elements (keys) / # of buckets

1. O(lambda)

2. O(N), only numerator grows

3. O(1), both numerator and denominator grow, so constant

4. O(n), cost of resizing since its linear putting elements into new indexes

5. O(1), averages out if we don’t resize array every single time a new element is added, but once every (multiple of array length, which is n) amount of elements are added.

Given an interface, state whether a lambda expression could be used to provide that interface.

Example: if ActionListener which only declares one abstract method named actionPerformed()

Topic: graphical user interfaces and lambda expressions

If an interface only declares a single method, then a lambda expression can be used wherever that interface is expected.

Example: yes we can!

Write a JUnit assertion to check that a given expression results in an exception being thrown.

From A4:

@Test
@DisplayName("Parsing an empty expression should throw an IncompleteRpnException")
void testParseEmpty() {
   //to parse an empty expression, we have to call RpnParser.parse("", Map.of())
}

@Test
@DisplayName("Parsing an empty expression should throw an IncompleteRpnException")
void testParseEmpty() {
    assertThrows(IncompleteRpnException.class, () -> RpnParser.parse("", Map.of()));
}

assertThrows(nameOfException.class, (param1, param2, …) - > method);

Write a lambda expression to be passed as an argument to a method expecting a functional interface.

1. write an expression for an ActionListener to print a message when a button is pressed.

   Information: ActionListener is a interface that has only one method: actionPerformed(Action Event e).

   You can print whatever you want.

2. write an expression for a Comparator to order students by age when sorting them.

b.addActionListener( e -> System.out.println("button clicked!");

• so the method addActionListener needs a listener, so we create an anonymous class that implements ActionListener.

• the interface ActionListener declare one method called actionPerformed. It needs an argument of type ActionEvent, so in the parenthesis we added a variable e that stands for the ActionEvent argument (type not needed to be explicity written).

• We put the - >

• The other side is the like the anonymous function. we negated the { } since its just one line.

(a,b) -> a.netId().compareTo(b.netId())

• can omit return since… actually i dunno i think java is just smart enough.

• the context is a bit effy, so this is just an expression to declare a functional interface (in this case, Comparator).

• note that compareTo is actually from Comparable :), this is because a.netId() returns Strings, which are Comparable.

Match a picture of a standard GUI widget to its name. Widgets could include labels, buttons, text fields, sliders, radio buttons, progress bars, and scroll bars.

All widgets extends JComponent

What is the structure of GUI? What is the root. What is each compoent object (in terms of JSwing)? What does it extend? What can we use in JSwing to group related controls?

(TODO somehow combine it with this bullet point:) Given a picture of a window containing bordered panels and standard widgets, sketch a hierarchy of how the components could be contained within one another (the frame will be at the root).

GUI is built from component objects with a tree structure.

• Root of tree = JFrame

each component object is a JComponent, this has its own data.

• JComponents extends Container. So think of this relationship as the parent (Container) and its children nodes (JComponents). These children are ordered.

we can group related controls into panels, which some sort of title-border.

• we can use JPanel

• Jframe does come with its own JPanel, but we can add more

• Default layout is all in one row

Given a snippet of Swing code that registers an event listener, identify the the event source, the event object, and the listener.

The event object is usually the parameter for a method.

The event source is usually like a JComponent thingy (like a Button) where we call .addNameListener on.

The event listener is whatever we call the method implements NameListener, (in some examples, its literally just JFrame)

Given a desired outcome (example: notify Swing that a component’s appearance needs to change), circle which painting-related method (e.g. repaint(), paintComponent()) should be called or overridden.

Topic: GUI and Lambda Expression

repaint(): CLIENT CALLS IT

• Request that this component be redrawn at the next opportunity, SO THIS WONT GET PAINTED RIGHT AWAY

• Most of your GUI code runs in event handlers – you are not in control

• so a bunch of event handles will call repaint(), and the program will bundle all these repaint()s and do then all at once at some point. Multiple events might necessitate repainting before the next screen refresh – don’t do redundant work

paint(): LET’S ACTUALLY PAINT! AND HOW TO PAINT!

• “Event handler” for “it’s time to draw yourself” events

• Declared in java.awt.Component

• Overridden by JComponent:

  • paintComponent: for custom components!

  • paintBorder()

  • paintChildren()

paintComponent() FOR CUSTOM COMPONENTS!!!

• Start with super.paintComponent()

there is somewhat of a difference between paint() and paintComponent(), but this isn’t something we are tested on. just treat them as the same.

race condition

Topic: Concurrrency

When a (mutable) object is shared between threads, its state (values of its fields) may change unexpectedly

• May change between lines of code

• May change while executing a single line of code

Sequential logic no longer guarantees correctness

• Invariants can be violated by someone else’s actions

Given an abbreviated reference for the API of Java’s Thread class, write code to execute a function on a new thread.

Topic: Concurrrency

So you have to use lambda function.

//as many param2 as the teask needs
Thread blah = new Thread( () -> nameOfTask(param1, param2));

//you need to start the thread at some point!
blah.start();

Mutex

Mututal Exclusion Locks

Only one thread may hold lock at a time

Other threads will block at the start of their synchronized block until the lock is available

so whatever is argument in synchronized(lock), is the mutex

Given a sequence of addition and removal operations made to a circular buffer with a specified capacity, draw the contents of its backing array after those operations have completed.

um… i kinda remembre from the lecture

• remember that get() take the first element, and removes it! FIFO!!! the next element in the ringbuffer is the new iHead!

Given a specification for the desired behavior of a class, and a partial implementation of the class, add code that uses condition variables (i.e., wait and notifyAll) to complete the implementation. The code you add causes threads to correctly synchronize by making some threads block and wait for others. Example: Barrier from DIS.

Think of the producer of fries, and the cusotmer who wants the fries!!

Ordered a fry but there aren’t any in the queue? call wait() and release and important locks. this needs to be in a while loop because there could be multiple customers asking for fries!

Produce a new fry! notifyAll() about the change!

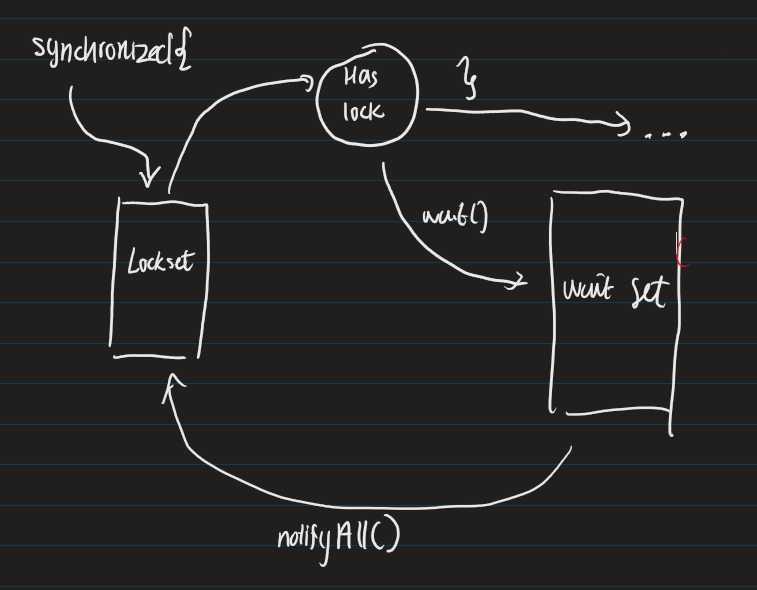
The Synchronized, lockset waitset diagram.

(I don’t think it’s necessary to memorize, but it’s really helpful for me for concurrency)

image

this is only for one thread though…. this could break if another thread 2 is concurrently accessing the same mutex, but it doesn’t have the synchronized block.

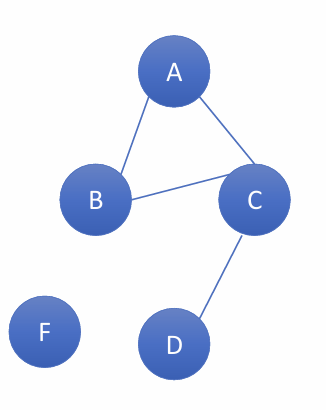
Example 1:

Given a drawing of a graph:

• write set of vertices, set of edges, state whether graph is directed or undirected (or the other way around)

topic: graphs

V = {A, B, C, F, D} (use curly brackets)

E = { {A,B}, {A,C}, {B, C}, {C,D} }

Undirected: order doesn’t matter

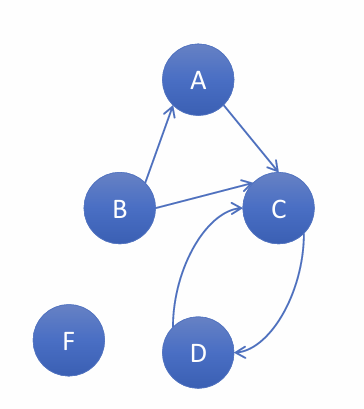
Example 2:

Given a drawing of a graph:

• write set of vertices, set of edges, state whether graph is directed or undirected (or the other way around)

topic: graphs

V = {A, B, C, D, F}

E = {(A,C), (B,A), (B,C), (C,D), (D,C)}

directed: order matters so use parenthesis ( )

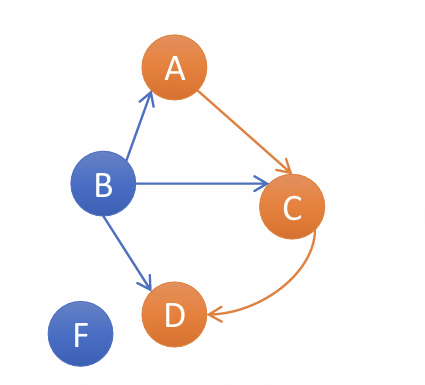
Given a drawing of a graph:

State whether a given sequence of vertices is a legal path in the graph. Or, write down all the paths in the (small) graph, and their lengths.

(A, C, D) ?

• note for directed its (v1, v2) and undirected its {v1, v2}

legal path

the length is the number of edges, so 3.

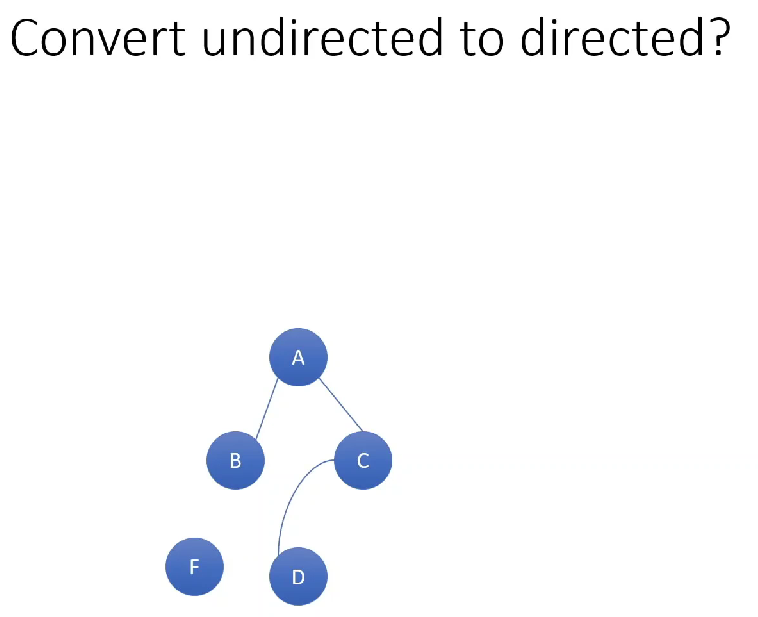
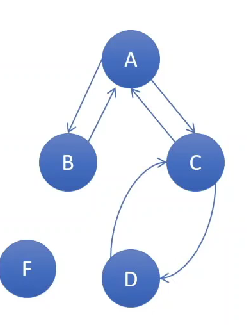
Given a drawing of a graph:

Redraw the graph, which now must be undirected, as a directed graph with the same set of vertices and paths.

Note: take each edge in undirected graph {u,v} and turn it in to 2 distinct pairs (u, v) and (v, u).

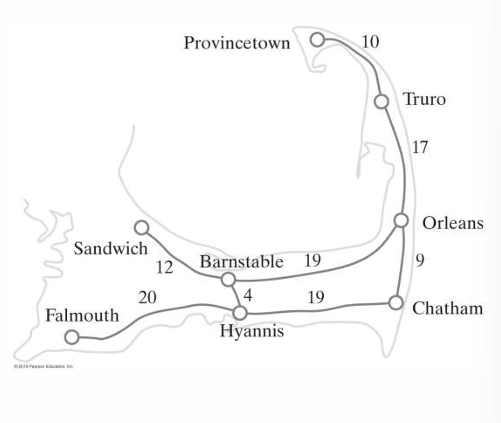
Given a drawing of a graph:

State the length and/or weight of a given path in the graph.

What is the length of the shortest path from Provincetown to Chatham?

What is the weight of the shortest path from Provincetown to Chatham?

length: number of edges; 3

weight: sum of all labels in a given path; 36

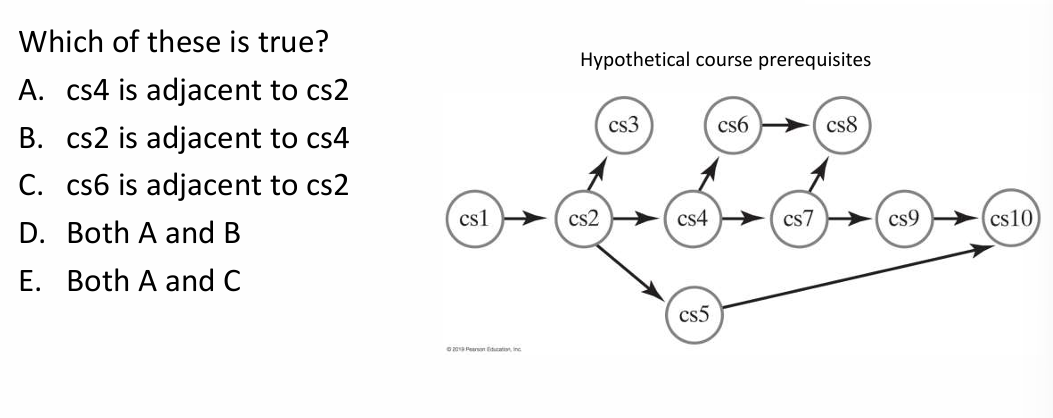
Example 1:

Given a drawing of a graph:

Circle which of several adjacency list representations corresponds to the drawing. Or vice-versa, given a representation, draw the graph, or circle which drawing is correct. Likewise, do the same for adjacency matrix representations.

Answer is A: cs4 is adjacent to cs2.

Example 2:

Given a drawing of a graph:

Circle which of several adjacency list representations corresponds to the drawing. Or vice-versa, given a representation, draw the graph, or circle which drawing is correct. Likewise, do the same for adjacency matrix representations.

(just read arrow from left to right)

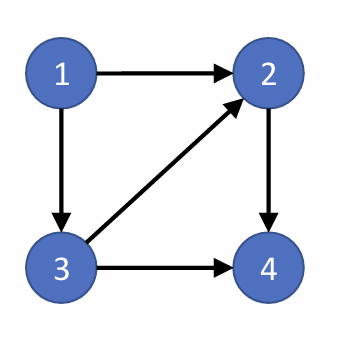
Example 3:

Given a drawing of a graph:

Circle which of several adjacency list representations corresponds to the drawing. Or vice-versa, given a representation, draw the graph, or circle which drawing is correct. Likewise, do the same for adjacency matrix representations.

A: B, C, D

B: None

C: None

D: A, C

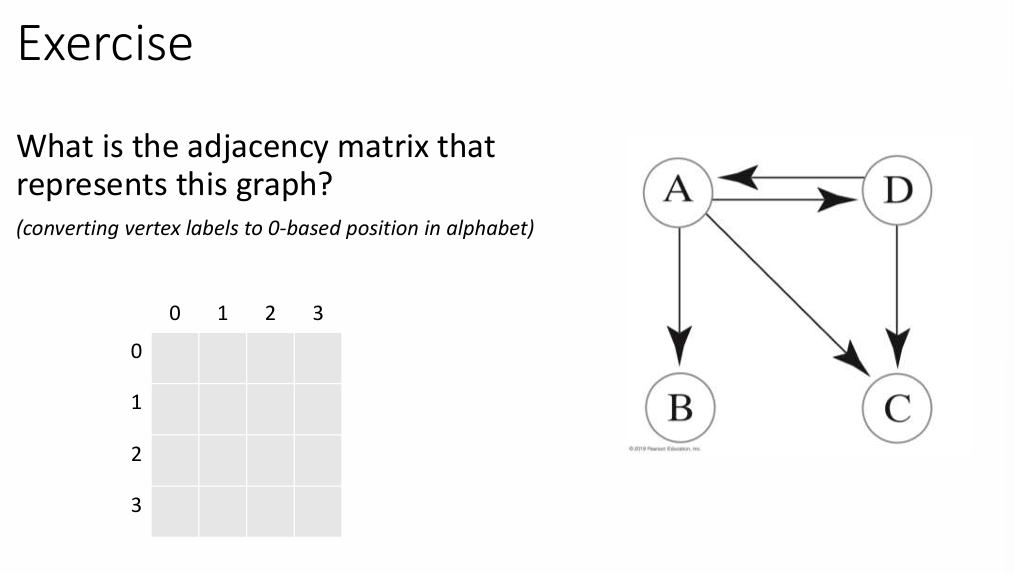
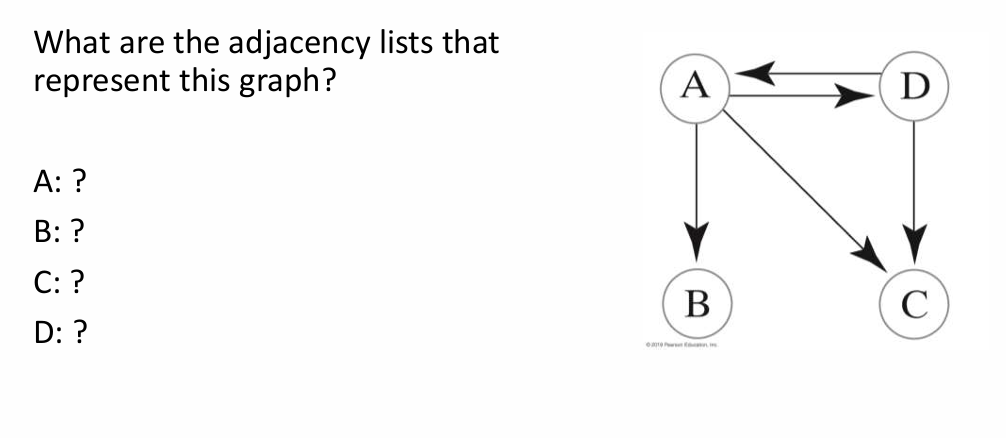
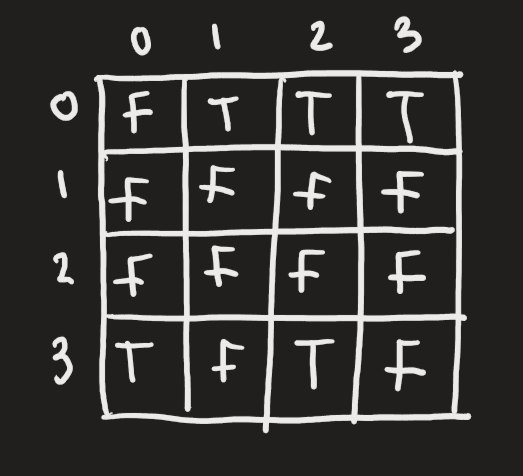
Example 4:

Given a drawing of a graph:

Circle which of several adjacency list representations corresponds to the drawing. Or vice-versa, given a representation, draw the graph, or circle which drawing is correct. Likewise, do the same for adjacency matrix representations.

remember that if there are labels, then instead of T/F, we put in the labels as the value in the 2d adjacency matrix.

Vertex u is adjacent to vertex v if ….

• u is adjacent to v: there is edge (undirect or directed) from v to u

v → u , this DOES NOT MEAN u → v !!!

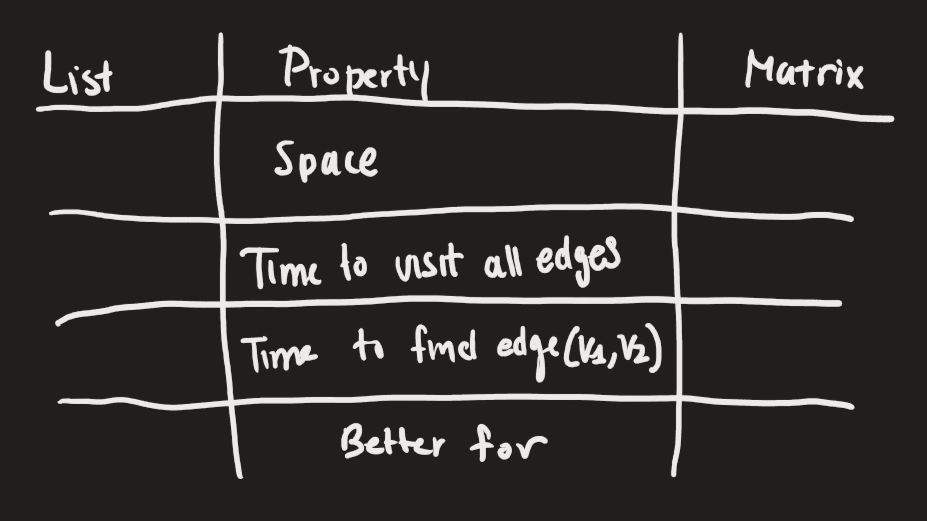
Given a representation (adjacency list or matrix), perform the following tasks:

• State in Big Oh notation the space requirements to store a graph using that representation, based on the number of vertices and edges

• Given some criteria—for example, about the size and density of the graph, and about which operations will be most frequent—choose the most suitable data structures to represent a graph. (If an adjacency list representation is most suitable, that could include choosing data structures for the vertex set and adjacency lists. → another flash card)

Okay for this just fill out this table

• Note that for matrix, we never use the edges in our calculations

• If are points are disconnected, then for the adjacency list, the big oh will eliminate E.

Example 1:

Given a representation (adjacency list or matrix), perform the following tasks:

• State the time and/or space complexity of an operation on the graph based on an English description of the operation, or on Java (pseudo)code implementing the operation. The operation might be one we studied, or it might be new. Your answer must be in the form of a Big Oh tightest bound.

Note that it says “there is an edge between every pair (u,v) of stops.”, so this is clearly a dense graph. we should use an adjacency matrix.

Given a representation (adjacency list or matrix), perform the following tasks:

• Given the fields and class invariant for implementing the representation, and given a specification for an operation, write the Java code for that. The operation might be one we studied, or it might be new.

Adjacency Lists:

i) Normal Graphs: usually consists of a Graph with Vertex. Each Vertex has a field (most likely LinkedList of Edge s . Each Edge has a starting vertex and a ending vertex.

usually when we want to traverse through the graph, we use an enhanced for-loop

//something like this
for( Edge e : v.outgoingEdges()){
   
}

Adjacency Matrix

Normal Graphs: usually consist of a Graph with a Set<Vertices>. Also a field that is 2d Edge[][].

For OOP Graphs:

• usually represent Vertex as its own objects and stored in a Map structure to quickly connect labels and vertexes.

• The Vertex object ITSELF holds the itereable sequences of Edges.

Given a representation (adjacency list or matrix), perform the following tasks:

• Given some criteria—for example, about the size and density of the graph, and about which operations will be most frequent—choose the most suitable data structures to represent a graph. If an adjacency list representation is most suitable, that could include choosing data structures for the vertex set and adjacency lists.

Sparsh graphs: adjacency lists

Dense graphs: adjacency matrix

Choices for adjacency lists:

• vertices(): Set<Vertices> and edges(): Set<Pair<V>> kinda sucks

• OOP: Each Vertex contains a Set of the vertices that are adjacent to it (adj). The Graph contains a Map of labels to Vertices (vertices) • "Object graph" resembles represented graph!

• Linked List (Easy to understand): a list of nodes, where each node has a label and an adjacency list of vertex labels.

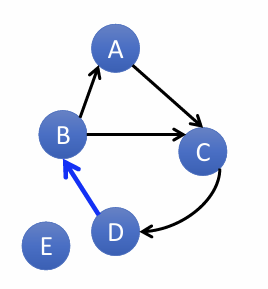
Given a diagram of a graph, state whether it is acyclic. If not, trace a path that forms a cycle.

I mean this is kinda easy

acyclic: never returns a visited node

this is CYCLIC, for example (D,B,C,D) is a cycle.

to check a more complicated graph, we can use topological sorting algorithm. find a vertex has has no incoming edges, remove that vertex and all of its outgoing edges. if in the end, there are no edges remaining among the vertices, then the thing is acyclic, i think.

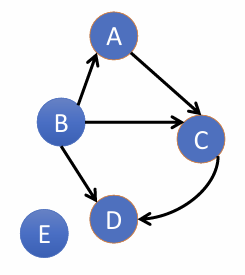
Example 1:

Given a diagram of a directed acyclic graph, state a topological ordering of its vertices. Or, circle which of several sequences of vertices correspond to a topological ordering.

E, B, A, C, D ← one example

note: if the topological sorting doesn’t include ALL the vertices in the graph, then it automatically isn’t valid.

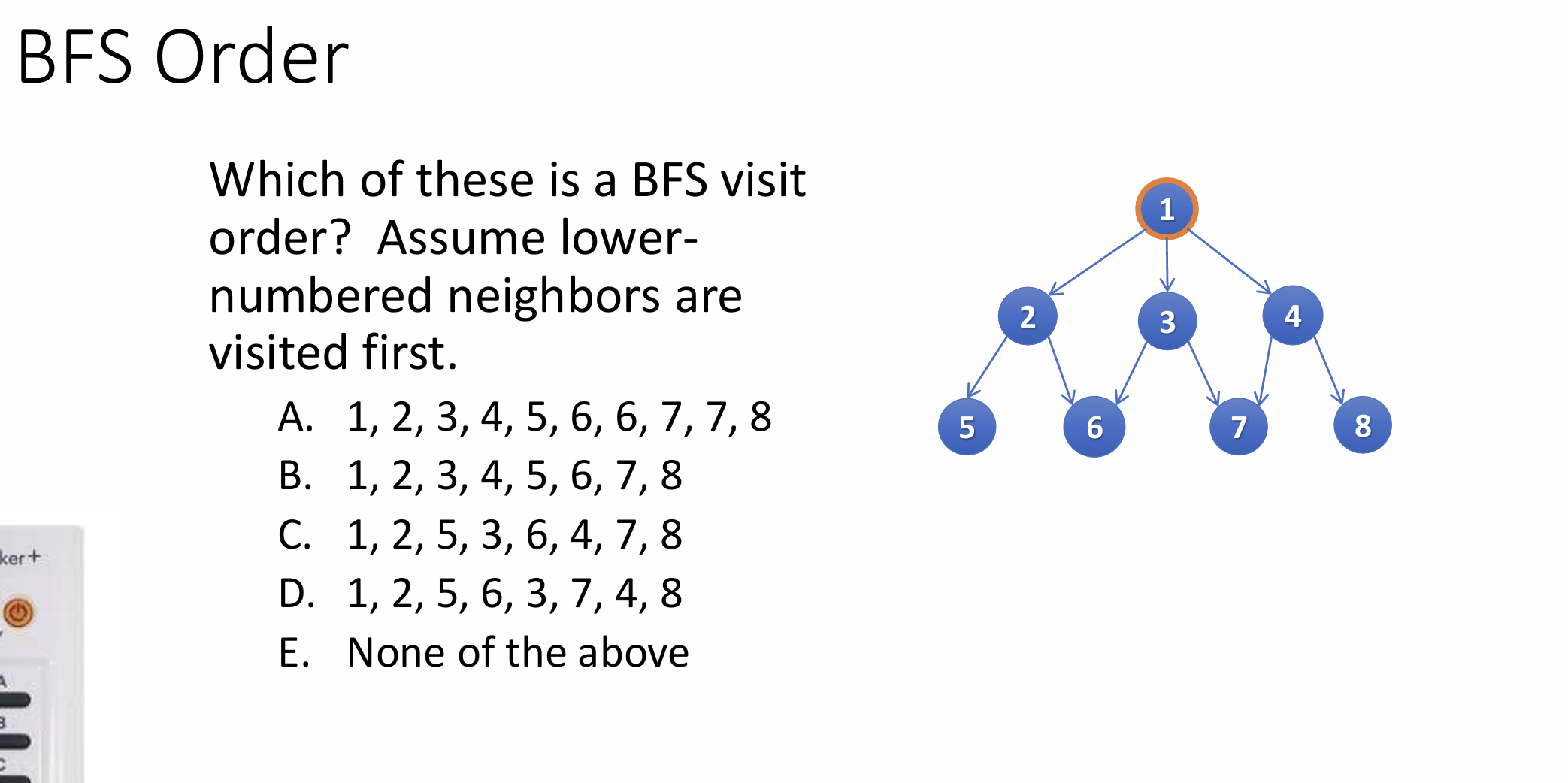
Example 1:

Given a diagram of a graph, a starting node, and a rule for the order in which neighbors are iterated (for example, alphabetical order by vertex label), state the order in which nodes are visited during a breadth-first or depth-first traversal. Or, state the order in which nodes are settled during a depth-first traversal.

Answer is B

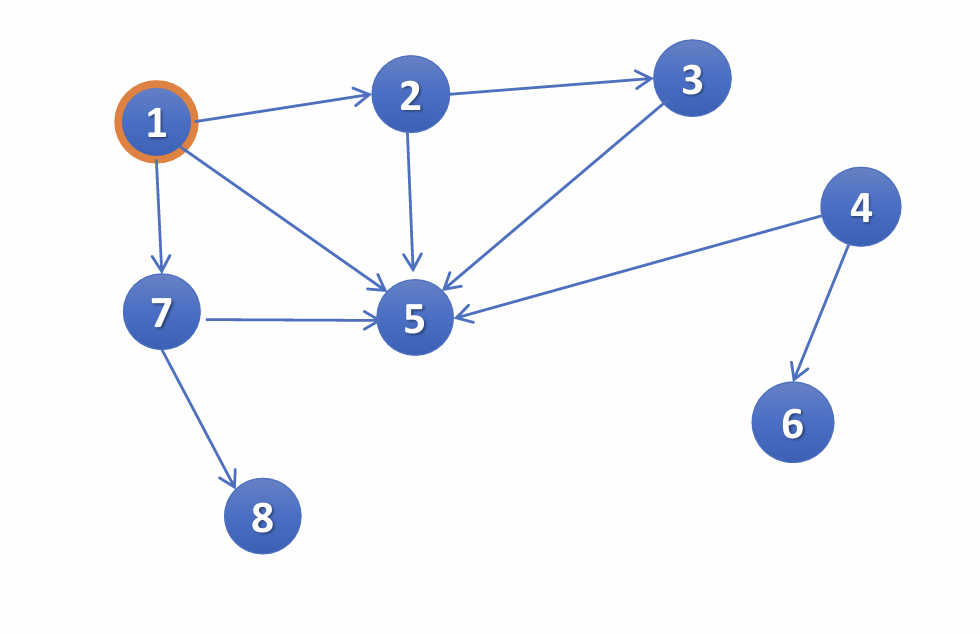
Example 2:

Given a diagram of a graph, a starting node, and a rule for the order in which neighbors are iterated (for example, alphabetical order by vertex label), state the order in which nodes are visited during a breadth-first or depth-first traversal. Or, state the order in which nodes are settled during a depth-first traversal.

State the order in which nodes are visited in this case… draw out the frontier and layers for each node.

we never reached 4 and 6 starting from 1.

if we want to continue until all nodes are reached, then 4 has layer 1, and 6 has layer 2.

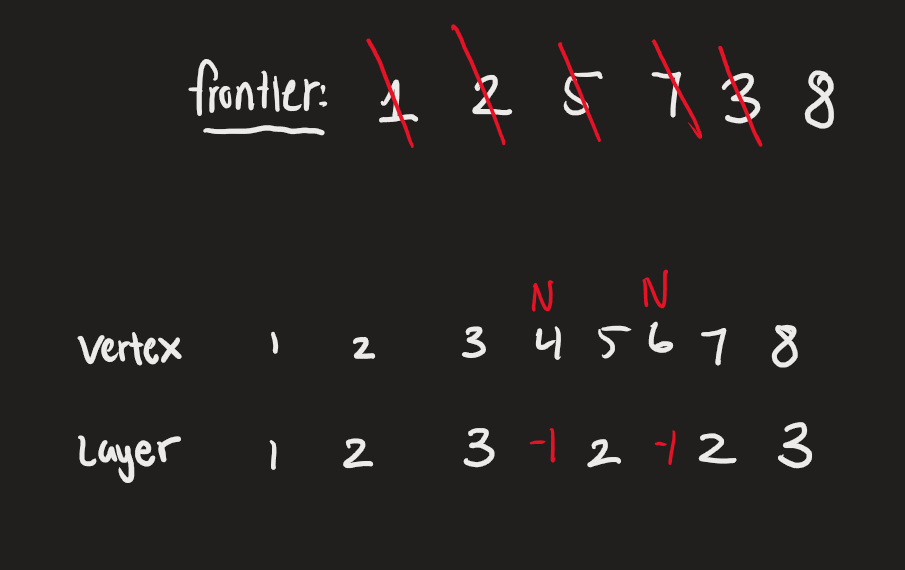
Example 3:

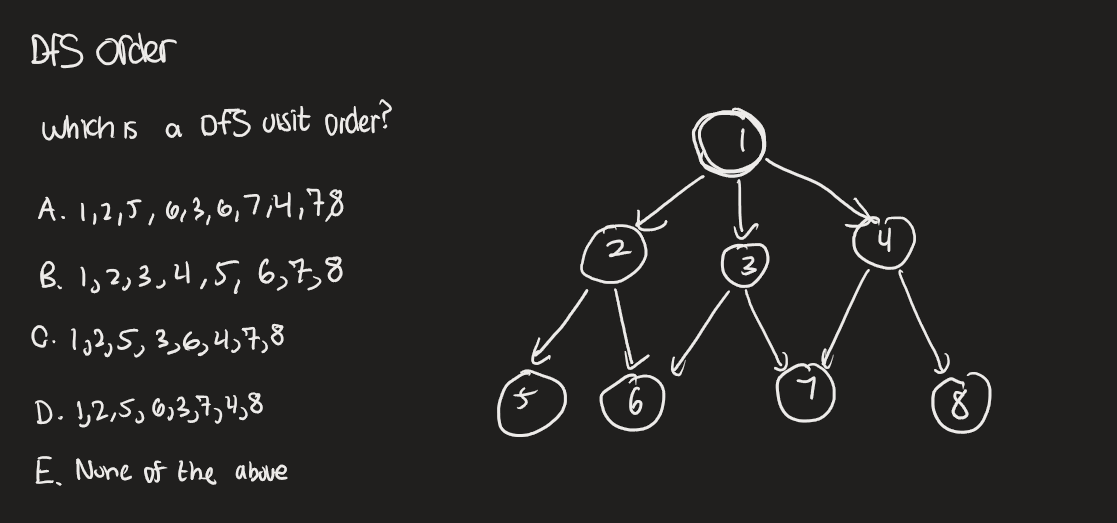
Given a diagram of a graph, a starting node, and a rule for the order in which neighbors are iterated (for example, alphabetical order by vertex label), state the order in which nodes are visited during a breadth-first or depth-first traversal. Or, state the order in which nodes are settled during a depth-first traversal.

D. 1, 2, 5, 6, 3, 7, 4, 8