Chap 6 Linear correlation, linear regression and organisation of data with more than one variable

Linear correlation, linear regression and organisation of data with more than one variable

Correlation

When the values of one variable vary systematically with respect to the values of the other (mutual

relationship).

Graphical representation of a relationship

Two-dimensional graphical representation

Two-dimensional graphical representation

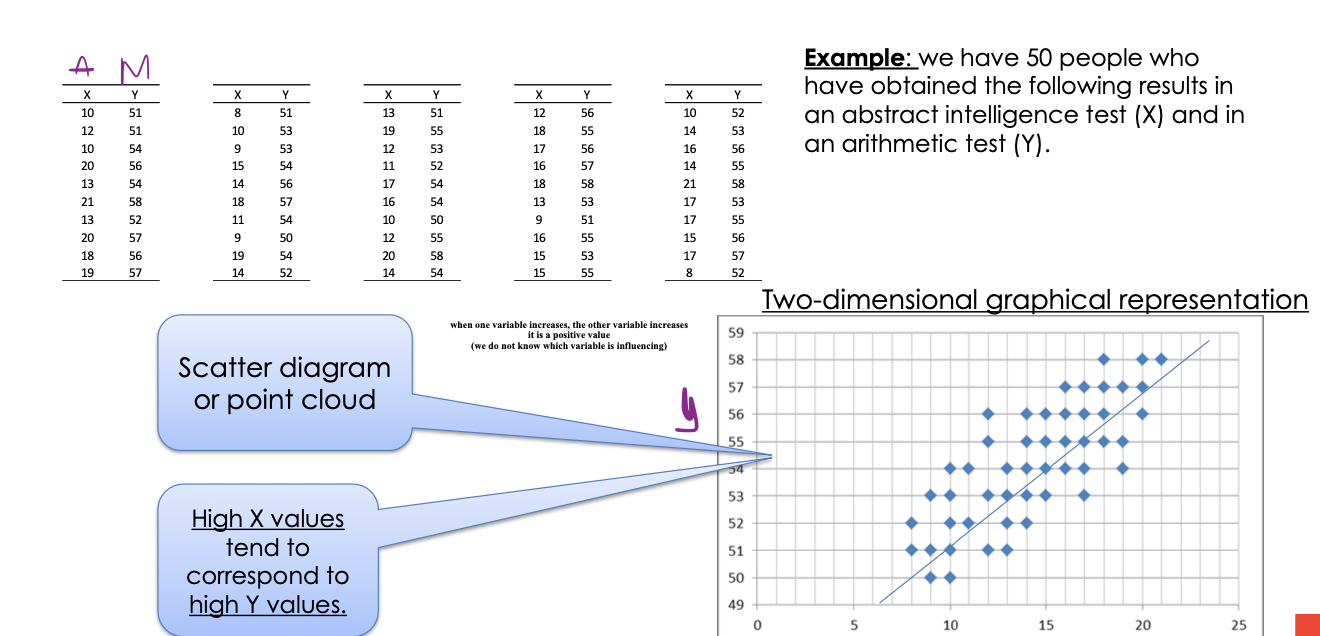
The simplest way to describe a two-dimensional distribution of a ratio is to represent the pairs of values in the Cartesian plane.

Graph of Linear correlation is called

point cloud or scatter plot

scatter plot

Graph of Linear correlation

Two-dimensional distributions

• The set of pairs of values corresponding to each individual when we study simultaneously the values of two variables in a population.

• Defined by two values (x,y)

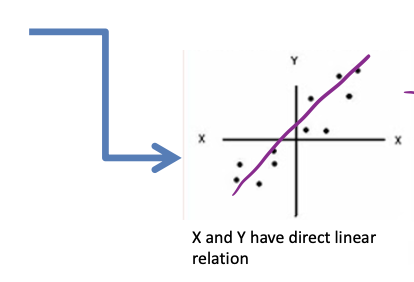
direct linear relationship

Two variables X and Y have a direct linear relationship when high values of X correspond to high values of Y and low values in X correspond to low values of Y.

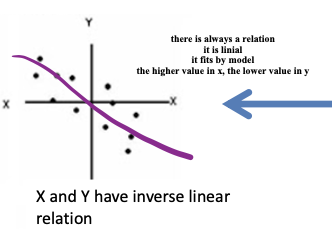
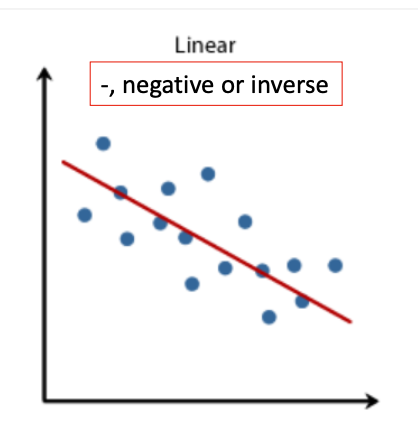
inverse linear relationship 

Two variables X and Y have an inverse linear relationship when high values of X correspond to low values of Y and low values of X correspond to high values of Y.

Two-dimensional graphical representation example

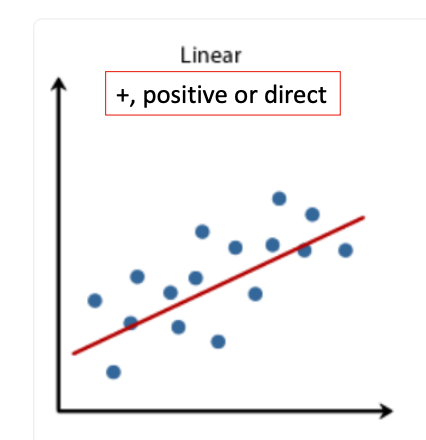
Scatter plots or point clouds are a tool for correlation analysis. (POSITIVE OR DIRECT)

Scatter plots or point clouds are a tool for correlation analysis. (NEGATIVE OR INVERSE)

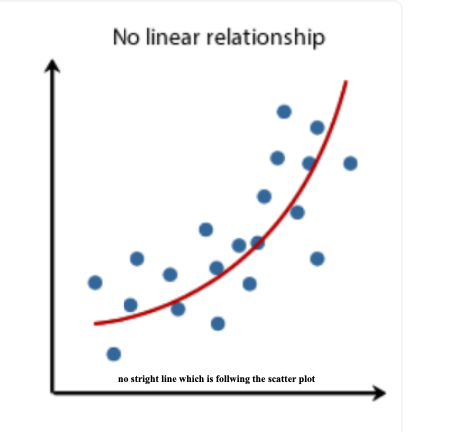
Scatter plots or point clouds are a tool for correlation analysis. (NO LINEAR RELATIONSHIP)

Quantification of a linear relationshi

Correlation analysis

Simple correlation analysis

Correlation coefficient

Correlation analysis

It measures and indicates the degree to which the values of one variable are related to the values of another.

Simple correlation analysis

Measures and indicates the degree of relationship between an independent variable and a dependent variable.

Correlation coefficient

• The value that quantifies the degree of correlation.

• The result of the correlation analysis.

formula for the correlation coefficient

we use something called the covariance.

covariance

This is almost exactly the same as the formula for variance, but instead of

multiplying scores by themselves we multiply the score on one variable (X) by the

score on the second variable (Y)

Sxy

Formula of coefficient

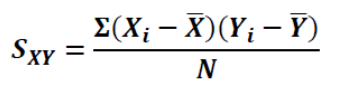
Covariance →

Sxy

• It indicates the degree of joint variation of two variables with respect to their mean

• → how much one variable moves when the other moves by the same amount.

Covariance → Sxy determines

• whether there is dependence between the two variables

Covariance → Sxy is necessary

• to stimate the regression line and the linear correlation coefficient.

Interpretation of covariance between X and Y

• If sxy > 0

• If sxy = 0

• If sxy < 0

sxy > 0,

• there is a direct (positive) covariance or relation

• therefore large values of x correspond to large values of y.

sxy = 0

• There is a no linear relation between the two studied variables.

• Lacks maximum and minimum values

If sxy < 0

• there is an inverse (negative) covariance or relation

• Therefore large values of x correspond to small values of y

rxy

• Pearson correlation coefficient

• Values between -1 and 1

Pearson Correlation Coeficient

• Is an index of how close the points on the scattergram fit the best-fitting straight line.

• A value near to 1.00 means that the points of the scattergram all lie exactly on the best-fitting straight line, or direct/positive linear relation.

• A value of 0.00 means that the points of the scattergram are randomly scattered around the straight line.

• To summarize: the closer the relationship between the two variables, the higher is the correlation coefficient, up to a maximum value of 1.00.

• value near to 1.00 means that the points

• means that the points of the scattergram all lie exactly on the best-fitting straight line, or direct/positive linear relation.

• A value of 0.00 means

• that the points of the scattergram are randomly scattered around the straight line.

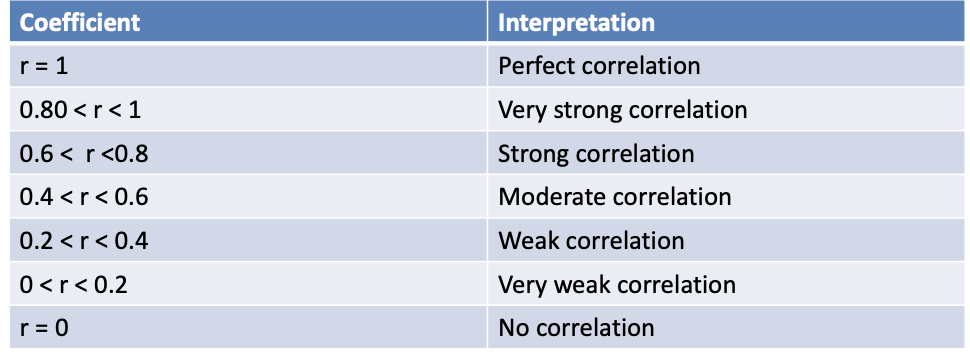
photo which indicates how strong or weak the correlation is

COEFFICIENT OF DETERMINATION:

The percentage of the variance of Y explained by X

rxy2

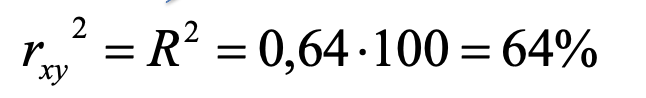
COEFFICIENT OF DETERMINATION

• Is an index of how much variance two variables have in common.

• The correlation coefficient is an index of how much variance two variables have in common

Why do we need to square the correlation coefficient?

• you need to square the correlation coefficient in order to know precisely how much variance is shared.

• The squared correlation coefficient is also known as the coefficient of determination.

A correlation coefficient of 0.64 means

that 64% of the variance is shared.

A correlation coefficient of 1.00 means

 100% of the variance is shared.

Some clarifications on the interpretation of the linear correlation coefficient

• It is recommended that it be interpreted together with the scatter diagram.

• The values it offers have to be interpreted according to the field of study (i.e. intelligence, personality, etc.) therefore relate with the field of study.

• Correlation coefficients are not sufficient to establish cause-consequence relationships between variables.

Correlation and variance and covariance matrices

• Useful for representing sets of variables and the quantification of their relationships

• The correlations/covariances of each variable with itself is always 1 (they do not appear in the matrix because they are redundant information).

• The matrix is symmetric with respect to the main diagonal; all values appearing above it are repeated again below it.

  • The reason is that, necessarily, rxy = ryx

Correlation and variance and covariance matrices (photo)

Interpreting the results

Reporting the results