Fluid transport KNW 2

force types in fluid mech

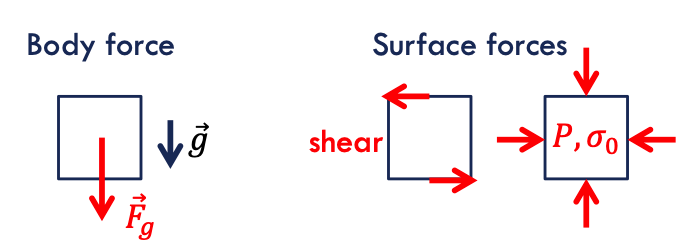
• body forces → associated with the presence of external fields acting equally on all fluid elements

• surface forces → acting on the surface of the control volume

reference systems

• Lagrange → development of a fluid package of constant mass

• Euler → mass flux through fixed volume

  • require local derivatives ads the property changes w/ time

• navier stokes eq → consider the velocity field that changes as function of time and space

fluid types

• inviscid = ideal fluids w/ no internal friction

• viscous = fluids w/ friction (resistance to shear)

  • newtonian → µ = const

  • non-newtonian → shear rate dependant t viscosity

equations of motion

• Euler equation: for ideal fluids considering gravity and normal stresses (pressure)

• Navier-Stokes equation: considers in addition viscous forces for Newtonian fluids.

• Stokes equation: derived from NS for stationary (steady state) flow.

hooks law

The force that is needed to extend or compress a spring is linear to the distance of elongation or compressions

stress types

• static → amount of deformation

  𝜎 = 𝑐 𝜀

  𝜎 = 𝑁/𝑚2

  𝜀 = 1

  𝑐 = stiffness tensor

• dynamic → rate of deformation

  𝜏 = 𝜇 𝜀

  𝜏 = 𝑁/𝑚2

  𝜀 = 1/𝑠

viscous stress force types

• Viscous forces with linear or volumetric dilation of fluid elements.

• Apparent viscous forces associated with dissipation during 1. → related to bulk viscosity of a compressible fluid.

• Surface forces associated with thermodynamic pressure

normal stress application cond

• Static conditions → thermodynamic pressure → 𝜎_𝑥 = 𝜎_𝑦 = 𝜎_𝑧

  (arithmetic average)

• Dynamic conditions → mechanical pressure → 𝝈_𝒙 = 𝒑 + 𝝉_𝒙𝒙

normal stress importance

• they can occur under static conditions – isotropic (thermodynamic) pressure

• They can occur under dynamic conditions:

  • In a deviatoric but purely non-deformable way (the principal shape is conserved) if the stresses are isotropic → bulk or volumetric viscosity

  • In a purely deformable way if the stresses are purely anisotropic → shear viscosity 𝜇.

heat capacity, C

the heat 𝑄 that is required to change the temperature by ∆𝑇

thermal diffusivity

measures the ability of a material to conduct thermal energy relative to its ability to store thermal energy

newtons 1st law of motion

an object either remains at rest or continues to move at a constant velocity 𝑢, unless acted upon by a force (constant momentum).

newtons 2nd law of motion

that rate of change of momentum of an object (body) is proportional to the net force applied to the object – the change is in direction of the applied force.

peclet number

dimensionless number describing the relative importance of advective to diffusive transport