Calculability and Complexity

This set of flashcards covers key concepts from calculability and complexity, including an intoduction, infinites sets, Turing machines, the lambda calculus and an introduction of complexity. It's designed to help review fundamental definitions, theorems, and relationships within the field of theoretical computer science.

Algorithme

un ensemble d’opérations de calcul élémentaires, organisées selon des règles précises dans le but de résoudre un problème donné.

Problème

une question générale dont la formulation contient typiquement plusieurs valeurs non spécifiées appelées paramètres.

Instance (d’un problème)

un problème dont on fixe les valeurs des paramètres.

Problème de décision

Un problème dont la réponse sera toujours soit oui soit non

Solution à un problème

Pour un problème particulier, soit A l’alphabet utilisé pour représenter les instances du problème, et B l’alphabet utilisé pour représenter leur solutions. La … au … est une fonction (éventuellement partielle) de A^{\ast}\to B^{\ast} .

Solution à une instance

Une valeur particulière lié au problème donné.

Calculable

Soit deux alphabets A et B. Une fonction (partielle) f:A^*→B^* est dite … s’il existe un algorithme qui, pour tout x∈A^*,

— s’arrête et produit f(x)∈B^* si f(x)↓;

— ne s’arrête pas si f(x)↑.

Modèle de calcul

Tout formalisme bien défini tant sur le plan syntaxique que sémantique dans lequel on peut décrire un algorithme.

Thèse de Church-Turing

Quel que soit le modèle de calcul (raisonnable) considéré, l’ensemble des fonctions calculables est le même.

Modèle de calcul universel

Un modèle de calcul dans lequel on peut calculer toutes les fonctions calculables.

Ensemble décidable

Soit X un ensemble et A⊆X. On dit que l’ensemble A est … (ou …) si il existe un algorithme qui, recevant en entrée un objet x∈X, s’arrête (tôt ou tard) et produit comme résultat « oui » si x∈A et « non » si x∉A.

Ensemble semi-décidable

Soit X un ensemble et A⊆X. On dit que l’ensemble A est … (ou …) si il existe un algorithme qui, recevant en entrée un objet x∈X, produit comme résultat « oui » si x∈A. Si x∉A, l’algorithme produit comme résultat « non » ou ne s’arrête pas.

Fonction caractéristique

Soit X un ensemble et A⊆X. La … … de A est une

fonction \chi_{A}\left(x\right):X\to\left\lbrace0,1\right\rbrace tel que

\chi_{A}\left(x\right)=\left\lbrace1\right.si x\in A et 0 si x\notin A

Soit X un ensemble, A ⊆ X et \chi_{A} : X → {0, 1} la fonction caractéristique de A. Alors

• A est décidable si et seulement si \chi_{A} est calculable et totale.

• A est semi-décidable si et seulement si \chi_{A} est calculable et dom(\chi_{A}) = A

Théorie de la calculabilité

L’étude de ce que l’on peut calculer par moyen algorithmique sans tenir compte des limites dues aux ressources disponibles.

Théorie de la complexité

L’étude de ce que l’on peut effectivement calculer en présence de ressources limitées, telles que le temps d’exécution et l’espace mémoire.

Complexité en temps (worst-case complexity)

Soit A un algorithme calculant une fonction L^*_1→L^*_2 pour des alphabets L_1 et L_2. La … en … de A est une fonction f:\mathbb{N}\to\mathbb{R} où

f(n)=max(\{T(w)|w∈L^*_1∧|w|=n\})

Complexité en espace (worst-case complexity)

La … en … de A est une fonction f^{\prime}:\mathbb{N}\to\mathbb{R} où

f^{\prime}(n)=max(\{E(w)|w\in L_1^{*}\land|w|=n\})

Complexité en temps (average-case complexity)

Soit A un algorithme calculant une fonction L^*_1→L^*_2 pour des alphabets L_1 et L_2. La … … en … de A est une fonction f^{}:\mathbb{N}\to\mathbb{R} où

f(n)=\sum_{w \in S}p(w)\cdot T(w)

avec S=\{w|w∈L∧|w|=n\} et p(w) représente la probabilité que l’entrée w soit choisie.

Complexité en espace (average-case complexity)

Soit A un algorithme calculant une fonction L^{\ast}_1\to L^{\ast}_2 pour des alphabets L_1 et L_2. La … … en … de A est une fonction f^{\prime}:\mathbb{N}\to\mathbb{R} où

f^{\prime}(n)=\sum_{w\in S}p(w)\cdot E(w)

avec S=\{w|w∈L∧|w|=n\} et p(w) représente la probabilité que l’entrée w soit choisie.

Complexité intrinsèque d’un problème

La complexité de l’algorithme le plus efficace connu pour résoudre ce problème.

Comportement asymptomatique de la complexité d’un algorithme

Soit T\left(n\right):\mathbb{N}\rightarrow\mathbb{R}^{+}

T(n)\in\mathcal{O}(f(n))\lrArr T(n) est asymptomatiquement bornée, par le dessus, par f(n) (à un facteur c près) :

\exists k\in\mathbb{N}:n\geq k\Rightarrow T(n)\leq cf(n)

T(n)\in\Omega(f(n))\lrArr T(n) est asymptomatiquement bornée, par le dessous, par f(n) (à un facteur c près) :

\exists k\in\mathbb{N}:n\geq k\Rightarrow T(n)_{}\geq cf(n)

T(n)\in\Theta(f(n))\lrArr T(n)\in\mathcal{O}(f(n))\land T(n)\in\Omega(f(n))

Problème efficacement soluble

Tout problème pour lequel il existe un algorithme de complexité polynomiale.

Problème intrinsèquement complexe

Tout problème pour lequel il n’existe pas d’algorithme de complexité polynomiale.

Relation d’ordre entre cardinaux d’ensemble

Soit deux ensembles A et B. Le cardinal de l’ensemble A est inférieur ou égal au cardinal de l’ensemble B, noté |A|≤|B| ssi il existe une fonction injective f:A→B.

Les ensembles A et B ont le même cardinal, noté |A|=|B| ssi il existe une fonction bijective f:A→B.

Ensemble dénombrable

Soit A un ensemble. A est dit … si A est un ensemble fini ou si |A|=|\mathbb{N}|.

Ensemble infini

Un ensemble A est dit …s’il a un sous-ensemble propre B ⊂ A tel que |B| = |A|.

Démonstration : Soit A un ensemble. A est dénombrable ssi il existe une fonction injective g : A → \mathbb{N}.

Démonstration

Démonstration : Soit A un ensemble. A est dénombrable ssi il existe une fonction surjective g : \mathbb{N} → A.

Démonstration

Démonstration : L’ensemble F = {f | f : \mathbb{N} → \mathbb{N} } est non-dénombrable.

Démonstration

Démonstration : Soit A un ensemble quelconque. On a

\left|A\right|\neq\left|P\left(A\right)\left|\right.\right.

Démonstration

Hypothèse du continu (de Cantor)

Hypothèse qui déclare qu'il n'existe pas d'ensemble infini dont la cardinalité est strictement comprise entre celle des entiers et celle des réels.

Soit \aleph_0=\left|\mathbb{N}\right| et \aleph_{}=\left|\mathbb{R}\right|. Soit \aleph_1 le plus petit cardinal strictement supérieur à \aleph_0 . Alors, on a : \aleph_1=\aleph .

Soit A, B des ensembles et g : A → B une fonction injective. Alors

1. si B est dénombrable, alors A est dénombrable

2. si A est non-dénombrable, alors B est non-dénombrable

   (+démonstration)

Soit A et B des ensembles tels que A ⊆ B.

1. si B est dénombrable, alors A est dénombrable

2. si A est non-dénombrable, alors B est non-dénombrable

Démonstration : L’ensemble \mathbb{N} × \mathbb{N} est dénombrable.

Démonstration

Fonction de couplage

Une fonction bijective qui mappe \mathbb{N} × \mathbb{N} vers \mathbb{N}, permettant d'encoder des paires d'entiers en un seul entier.

Projections

Étant donné une fonction de couplage \pi , on appelle … associées à \pi les fonctions \pi_0:\mathbb{N}\to\mathbb{N} et \pi_1:\mathbb{N}\to\mathbb{N} définies de façon que \pi_0\left(\pi\left(x,y\right)\right)=x et \pi_1\left(\pi\left(x,y\right)\right)=y

pour x,y\in\mathbb{N} .

Soit \pi une fonction de couplage et soit k\in\mathbb{N},k\ge1. On définit \pi^{k}:\mathbb{N}^{k}\to\mathbb{N} par induction :

\pi^1\left(x\right)=x
\pi^{k}\left(x_0,\ldots,x_{k-1}\right)=\pi\left(\pi^{k-1}\left(x_0,\ldots,x_{k-2}\right),x_{k-1}\right) pour k>1

Soit \pi une fonction de couplage et soit i,k\in\mathbb{N},k\ge1 et 0\le i\le k . On définit \pi_{i}^{k}:\mathbb{N}^{}\to\mathbb{N} par induction :

1. \pi_0^1\left(x\right)=x

2. \pi_{i}^{k}\left(x_{}\right)=\pi_{i}^{k-1}\left(\pi_0\left(x\right)\right) pour k>1 et i<k-1

3. \pi_{i}^{k}\left(x_{}\right)=\pi_1\left(x\right) pour k>1 et i=k-1

Relation formelle couplage-projections à k dimensions

Soit \left(x_0,\ldots,x_{k-1}\right)\in\mathbb{N}^{k}. On a

1. x_{i}=\pi_{i}^{k}\left(\pi^{k}\left(x_0,\ldots,x_{k-1}\right)\right) pour i<k

2. x=\pi^{k}\left(\pi_0^{k}\left(x\right),\ldots,\pi_{k-1}^{k}\left(x\right)\right) pour x\in\mathbb{N}

Etant donnée une fonction de couplage \pi, on définit la fonction \varphi_{\pi}:\mathbb{N}^{\ast}\to\mathbb{N}

\varphi_{\pi}\left(\epsilon\right)=0

\varphi_{\pi}\left(x_0,\ldots,x_{k-1}\right)=1+\pi\left(k,\pi^{k}\left(x_0,\ldots,x_{k-1}\right)\right)

Démonstration : Soit A un ensemble dénombrable. Alors A^{k} est dénombrable (pour k\in\mathbb{N} ) et A^{\ast} est dénombrable

Démonstration

Codage

Soit A, B des ensembles. Un … de A en B est une fonction injective c : A → B telle que

\forall a\in A:c^{-1}\left(c\left(a\right)\right)=a

Réalisation selon un codage

Une fonction g : B → B réalise une fonction f : A → A selon c si \forall a\in A on a

f\left(a\right)=\bot\Rightarrow g\left(c\left(a\right)\right)=\bot

f\left(a\right)\ne\bot\Rightarrow g\left(c\left(a\right)\right)=c\left(f\left(a\right)\right)

Encodage dans \mathbb{N}

Soit f:A^{\ast}\to A^{\ast} une fonction calculable pour un alphabet A.

Alors il existe un encodage c:A^{\ast}\to\mathbb{N} et une fonction calculable f^{\prime}:\mathbb{N}\to\mathbb{N} tel que f’ réalise f selon c.

Ensemble effectivement énumérable

Soit L un langage sur un alphabet \Sigma , donc L\subseteq\Sigma^{\ast}. L est dit … ssi il existe un algorithme qui énumère, de façon structurée et exhaustive, tous les éléments de L .

Enumération de L

Suite \langle w_1,w_2,w_3...\rangle comprenant tous les mots de L.

Démonstration : Soit L\subseteq\Sigma^{\ast}un langage quelconque sur l’alphabet \Sigma. Alors L est effectivement énumérable ssi Lest semi-décidable.

Démonstration

Langage de programmation

Un … L comprend

• un couple d’ensembles (P_{L},D_{L} ) où P_{L} représente l’ensemble de tous les programmes écrits en L et D_{L} l’ensemble de tous les objets qu’un programme de P_{L} peut manipuler

• une fonction [[.]]^{L}:P_{L}\to\left(D_{L}\to D_{L}\right) qui représente la sémantique du langage.

Couplage

Soit L un langage de programmation et D_{L} le domaine de données manipulées par L. Le langage permet le … si et seulement si D_{L}\times D_{L}\subseteq D_{L}

Syntaxe concrète

Soit L=\left(P_{L},D_{L}\right) un langage de programmation. L admet une … … si et seulement si P_{L}\subseteq D_{L}

Fonction calculable (pour langage de programmation)

Soit L=\left(P_{L},D_{L}\right) un langage de programmation. Une fonction (partielle) f:D_{L}\to D_{L} est dite … par L s’il existe un programme P\in P_{L} tel que pour tout t\in D_{L} :

• si f\left(t\right)=t^{\prime} alors [[P]]^{L}t\downarrow et [[P]]^{L}t=t^{\prime}.

• si f\left(t\right)\uparrow alors [[P]]^{L}t\uparrow.

Ensemble décidable (pour langage de programmation)

Soit L un langage de programmation et soit A\subseteq D_{L}.

On appelle l’ensemble A … (ou …) relatif à L si il existe un programme P\in P_{L} tel que [[P]]^{L}(x)\downarrow pour tout x\in D_{L} et [[P]]^{L}(x)=true ssi x\in A .

Ensemble semi-décidable (pour langage de programmation)

Soit L un langage de programmation et soit A\subseteq D_{L}.

On appelle l’ensemble A … (ou … …) relatif à L si il existe un programme P\in P_{L} tel que [[P]]^{L}(x)=true ssi x\in A .

Fonction d’interprétation

Soit L=\left(P_{L},D_{L}\right)et M=\left(P_{M},D_{M}\right) deux langages de programmation. En supposant que L permette le couplage et que \left(P_{M}\cup D_{M}\right)\subseteq D_{L}.

On appelle … d’… de M par L une fonction partielle i:D_{L}\to D_{L} telle que \forall P\in P_{M}:\forall t\in D_{M}:[[P]]^{M}t=i(P,t)

Interpréteur

Soit L=\left(P_{L},D_{L}\right)et M=\left(P_{M},D_{M}\right) deux langages de programmation. En supposant que L permette le couplage et que \left(P_{M}\cup D_{M}\right)\subseteq D_{L}.

On appelle … de M par L un programme int \in P_{L} tel que [[int]]^{L} est une fonction d’interprétation de M par L.

Fonction de compilation

Soit L=\left(P_{L},D_{L}\right), M=\left(P_{M},D_{M}\right) et T=\left(P_{T},D_{T}\right) trois langages de programmation et soit c un codage de D_{M} en D_{T}. En supposant que \left(P_{M}\cup D_{M}\right)\subseteq D_{L}.

On appelle … de … de M en T selon c une fonction totale t:D_{L}\to D_{L} telle que \forall P\in P_{M}:[[f\left(P\right)]]^{T} réalise [[P]]^{M} selon c

Compilateur

Soit L=\left(P_{L},D_{L}\right), M=\left(P_{M},D_{M}\right) et T=\left(P_{T},D_{T}\right) trois langages de programmation et soit c un codage de D_{M} en D_{T}. En supposant que \left(P_{M}\cup D_{M}\right)\subseteq D_{L}.

On appelle … de M en T selon c un programme comp\in P_{L} tel que [[comp]]^{L} est une fonction de compilation selon c.

Simulation d’un langage

Soit L=\left(P_{L},D_{L}\right), M=\left(P_{M},D_{M}\right) des langages de programmation. On dit que L peut … M s’il existe un codage c de D_M en D_L tel que \forall P\in P_{M}:\exists Q\in P_{L} tel que [[Q]]^L réalise [[P]]^M relativement à c

Programme universel

Soit L=\left(P_{L},D_{L}\right) un langage de programmation. On appelle … … pour L un interpréteur de L en L (noté sint).

Démonstration : Soit L=\left(P_{L},D_{L}\right) un langage de programmation non-trivial. Soit sint un interpréteur de L en L. Alors [[sint]]^L est une fonction partielle.

Démonstration

Démonstration : Problème de l’arrêt

Soit L=\left(P_{L},D_{L}\right) un langage de programmation non-trivial qui admet le couplage et une syntaxe concrète. La fonction totale h:D_L→{true,false} définie comme h(p,t)={true\cdot si\cdot[[p]]^{L}(t)\downarrow};false\cdot sinon n’est pas calculable en L

Démonstration

Propriété de programmes

Soit L=\left(P_{L},D_{L}\right) un langage de programmation. On appelle … des programmes en L un sous-ensemble A\subseteq P_{L}.

Propriété non-triviale existentielle

Soit L un langage de programmation. Soit A une propriété des programmes en L. On dit que A est … si A\ne\varnothing et A\ne P_{L}.

On dit que A est … si pour P,Q\in P_{L} tel que [[P]]=[[Q]] on a P\in A ssi Q\in A.

Démonstration : Théorème de Rice

Soit L un langage de programmation et A une proriété non-triviale et existentielle des programmes en L. Alors A est indécidable.

Démonstration

Fonction de spécialisation

L=\left(P_{L},D_{L}\right) avec couplage et syntaxe concrète. Une … de … pour L est une fonction m:D_L→D_L tel que pour tout programme P\in P_L et s\in D_L,m(P,s)\in P_L et \forall d\in D_{L}:[[m(P,s)]]d=[[P]](s,d)

Spécialisateur

Un programme spec est un … si [[spec]] est une fonction de spécialisation

Démonstration : Soit S=\left(P_{S},D_{S}\right) , T=\left(P_{T},D_{T}\right) deux langages de programmation. Soit int_S un interpréteur pour S écrit en T, et soit spec_T un spécialisateur pour T. Alors comp=[[spec_T]]^T(spec_T,int_S) est un compilateur de S en T.

Démonstration

Théorème du point fixe

Soit L=\left(P_{L},D_{L}\right) un langage de programmation universel et f:P_L→P_L totale et calculable. Il existe un programme P\in P_L tel que [[P]]^L=[[f(P)]]^L

Théorème du point fixe (bis)

Soit L=\left(P_{L},D_{L}\right) un langage de programmation. Pour tout programme P,\exists Q tel que \forall t\in D_{L}

[[Q]]t=[[P]](Q,t)

Démonstration : Théorème de Rice (sur base du point fixe)

Soit L un langage de programmation et A une proriété non-triviale et existentielle des programmes en L. Alors A est indécidable.

Démonstration

Syntaxe du lambda calcul

⟨expression⟩ ::= ⟨var⟩∣⟨abstraction⟩∣⟨application⟩∣(⟨expression⟩)

⟨abstraction⟩ ::= λ⟨var⟩.⟨expression⟩

⟨application⟩ ::= ⟨expression⟩⟨expression⟩

où ⟨var⟩ = x,y,z,…

Variable liée

Une occurrence d’une variable x dans une expression est … quand elle figure dans le corps e d’une abstraction \lambda x.e.

Variable libre

Une occurrence d’une variable x dans une expression est … au sein d’une expression si elle ne fait pas partie du corps e d’une abstraction \lambda x.e.

\alpha-conversion

Une abstraction (\lambda x.e) est équivalente à (\lambda x.e_0) ssi les conditions suivantes sont vérifiées :

• il n’y pas d’occurrences libres de y dans e , ni de x dans e_0.

• e se transforme en e_0 en remplaçant chaque occurrence liée de x par y, et vice-versa.

Rédex

On appelle … d’une expression toute sous-expression ayant la forme (\lambda x.e)e_0, c’est-à-dire une application dont la première partie est une abstraction.

\beta-réduction

Le rédex se réduit à l’expression que l’on obtient en remplaçant dans e toutes les occurrences liées de x par e’.

De façon générale, on dit qu’une expression e_1 se réduit à e_2, noté e_1 \xrightarrow{\beta} e_2

si on obtient e_2 à partir de e_1 en remplaçant dans cette dernière expression l’un de ses rédex par le résultat de réduction. On appelle … ce type de réduction.

Théorème de Church-Rosser

Soit e une expression. Si e\xrightarrow{\beta^{\ast}}e_1 et e\xrightarrow{\beta^{\ast}}e_2 et e_1\neq e_2 alors il existe une expression e’ telle que e_1\xrightarrow{\beta^{\ast}}e^{\prime} et e_2\xrightarrow{\beta^{\ast}}e^{\prime}

Entiers naturels (redex)

0\equiv\lambda sz.z

1\equiv\lambda sz.sz

2\equiv\lambda sz.\left(s\left(sz\right)\right)

3\equiv\lambda sz.\left(s\left(s\left(sz\right)\right)\right)

Successeur (redex)

S\equiv\lambda wyx.y\left(wyx\right)

Addition (redex)

Add\equiv\lambda xy.xSy

Multiplication (redex)

Mul\equiv\lambda xy.x\left(Addy\right)0

Exponentiation (redex)

Exp\equiv\lambda mntq.m\left(Muln\right)1

Exp\equiv\lambda mntq.nmtq=\lambda mn.nm

Valeurs booléennes (redex)

T\equiv\lambda xy.x

F\equiv\lambda xy.y

L’opération ET (redex)

\land\equiv\lambda xy.xyF

L’opération OU (redex)

∨ ≡ λxy. x T y

La négation (redex)

\lnot\equiv\lambda x.xFT

If Then Else (redex)

IfThenElse\equiv\lambda pab.pab

Structures de données (redex)

Cons ≡ λxy. (λz. z x y)

Head ≡ λp. p T

Tail ≡ λp. p F

Comparaison avec zéro (redex)

Z ≡ λx. x F ¬ F

Z\equiv\lambda x.x\left(\lambda y.F\right)T

Prédécesseur (redex)

Φ ≡ λp.(λz.z(S(p T ))(p T ))

P red ≡ λn.n Φ (Cons 0 0) F

Opérateur point fixe (redex)

Y ≡ λy.(λx.y(xx))(λx.y(xx))

Représentation des données (syntaxe concrète)

Soit \char"0190 l’ensemble des expressions en lambda calcul. On définit la fonction de représentation \lceil\rceil:\char"0190 \to\char"0190 comme suit :

\lceil x\rceil\equiv\lambda abc.ax

\lceil mn\rceil\equiv\lambda abc.b\lceil m\rceil\lceil n\rceil

\lceil\lambda x.m\rceil\equiv\lambda abc.c\left(\lambda x.\lceil m\rceil\right)

Interpréteur sint (lambda calcul)

sint\equiv YE

E\equiv\lambda rp.pfgh où

• f=\lambda x.x

• g=\lambda xy.\left(rx\right)\left(ry\right)

• h=\lambda z.\lambda v.r\left(zv\right)

Automate fini déterministe

M=(Q,\Sigma,\delta,q_0,F) où

• Q est un ensemble fini d’états

• \Sigma est un alphabet

• \delta:Q\times\Sigma\to Q est la fonction de transition

• q_0\in Q est l’état initial

• F\subseteq Q est l’ensemble des états finaux

Automate à pile

M=(Q,\Sigma,\Gamma,\Delta,Z,q_0,F) où

• Q est un ensemble fini d’états

• \Sigma est l’alphabet du ruban

• \Gamma est l’alphabet de la pile

• \Delta:\left(Q\times\Sigma^{*}\times\Gamma^{*}\right)\to\left(Q\times\Gamma^{*}\right) est la fonction de transition

• Z est le symbole de fin de pile

• q_0\in Q est l’état initial

• F\subseteq Q est l’ensemble des états finaux

Machine de Turing

M=(Q,\Gamma,\Sigma,\delta,q_0,B,F) où

• Q est un ensemble fini d’états

• \Gamma est l’alphabet du ruban

• \Sigma\subseteq\Gamma est l’alphabet d’entrée

• q_0\in Q est l’état initial

• F\subseteq Q est l’ensemble des états finaux

• B \in (\Gamma \setminus \Sigma) est le «blanc» que l’on dénote le plus souvent par #

• \delta:\left(Q\times\Gamma\right)\to\left(Q\times\Gamma\times\left\lbrace L,R^{}\right\rbrace\right) est la fonction de transition

Dérivable en une étape (MdT)

(q,w,v)\vdash_{M}(q’,w’,v’)

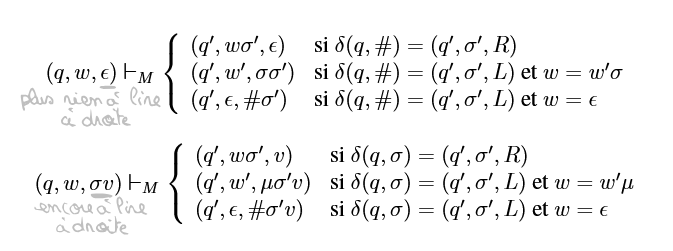
Dérivable en plusieurs étapes

(q,w,v)\vdash^{\ast}_{M}(q’,w’,v’)

s’il existe k>0 configurations {(qi, wi, vi) | 1 ≤ i ≤ k} tels que (q_0,w_0,p_0)=(q,w,v), (q_{k},w_{k},p_{k})=(q^{\prime},w^{\prime},v^{\prime}) et (q_{i},w_{i},v_{i})\vdash_{M}^{\ast}(q_{i+1},w_{i+1},v_{i+1}) pour tout 0\le i\le k.

Langage accepté

L(M)={w\in\Sigma^{*}|(q_0,\epsilon,w)\vdash^{\ast}_{M}(q,v,v^{\prime})} avec q\in F et v,v’\in\Gamma^{\ast}\rbrace