Chapter 10: Correlation and Regression

Correlation Analysis

Statistical study of the strength and direction of the relationship between two quantitative variables.

Scatterplot (Scatter Diagram)

A two-dimensional graph that plots individual paired observations to visualize the possible relationships between two variables.

Positive Linear Correlation

Relationship in which an increase in one variable corresponds to increases in the other variable.

Negative Linear Correlation

Relationship in which an increase in one variable correspond to decreases in the other variable.

No Linear Correlation

Situation where an increase in one variable has no consistent impact on the other variable.

Linear Correlation Coefficient (ρ)

A summary measure that denotes the strength of the linear relationship existing between two variables (say X and Y), that is independent of the respective scales of measurement

• denoted by 𝜌 (lowercase Greek letter rho

Formula of the Linear Correlation Coefficient

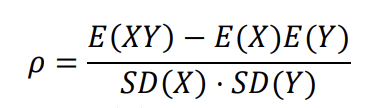
Properties of the linear correlation coefficient

• −1 ≤ ρ ≤ 1

  • positive value means that the line slopes upward (to the right)

  • negative value means that the line slopes downward (to the right)

• ρ = 0 → no linear coefficient

• p = -1 or +1 → perfect linear relationship

• p close to 1 or -1 → strong linear relationship

Pearson Product-Moment Correlation Coefficient (r)

Sample statistic that estimates ρ; calculated from paired data to quantify linear association.

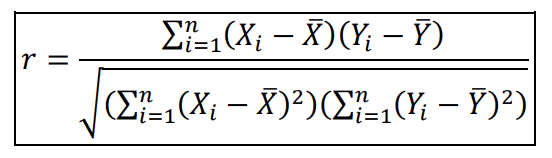
Computational formula for r

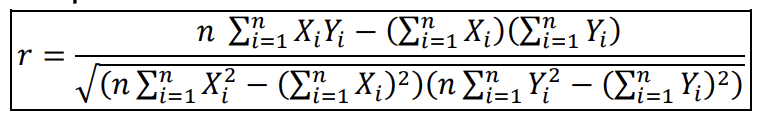
Perfect Linear Correlation

Case where ρ = ±1 and every data point falls exactly on a straight line.

Hypothesis Test for ρ

Uses test statistic T = (r − ρ₀) / √[(1 − r²)/(n − 2)] with t-distribution (n − 2 df) to assess a specified population correlation.

Correlation Does Not Imply Causation

Strong association alone cannot establish that one variable causes changes in another; third factors or coincidence may exist.

Simple Linear Regression Model (SLRM)

A probabilistic model that relates a response variable Y to an explanatory variable X via a linear function plus random error. → Yᵢ = β₀ + β₁Xᵢ + εᵢ

Response Variable (Y)

Outcome being predicted or explained in regression analysis.

Explanatory Variable (Predictor, X)

Variable used to predict or explain changes in the response variable.

Regression Coefficient β₀

Y-intercept of the regression line → expected value of Y when X = 0 (may be uninterpretable if 0 is outside data range).

Regression Coefficient β₁

Slope of the line; expected change in mean Y for a one-unit increase in X.

Random Error Term (εᵢ)

A representation of the effect of unobserved factors that affect the response variable to some extent; assumed:

• independent,

• normally distributed

• mean 0

• constant variance σ²

Random distribution of Y variable in the simple linear regression model

𝑌_𝑖 = 𝛽₀ + 𝛽₁𝑋_i + 𝜀_i, where 𝜀_i~Normal(0, 𝜎²)

Regression Equation

E(Y) = 𝛽₀ + 𝛽₁x_i

Least Squares Method

Estimation technique that chooses β̂₀ and β̂₁ to minimize the sum of squares of the deviations of the observed value of Y from its expected value (choosing the “best-fitting” line that fits all data points as much as possible).

Least of Squares Estimators

𝑏₁ = 𝛽̂₁ and 𝑏₀ = 𝛽̂₀ are given as follows:

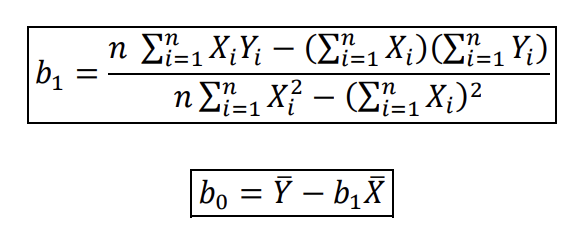
On Extrapolation of the Regression Model

The estimated regression equation is appropriate only for the relevant range of X.

Testing if there is no linear relationship between Y and X

Hypothesis Test → Ho: 𝛽1 = 0 versus Ha: 𝛽1 ≠ 0.

Confidence Interval → construct a confidence interval for 𝛽1 and check if it contains 0

Residual (dᵢ)

Difference between observed and predicted response: dᵢ = Yᵢ − Ŷᵢ.

Coefficient of Determination (R²)

Proportion of the variability in the observed values of the response variable Y that can be explained by the explanatory variable X through their linear relationship

Purpose of the Coefficient of Determination

Used to assess the goodness-of-fit of the linear regression model

Range of the Coefficient of Determination (R²)

R² = r² (0 ≤ R² ≤ 1)

• Perfect probability = 1

• No predictive capability = 0

Interpretation of the Coefficient of Determination

An R² of __ means that __% of the variance/variability in Y can be predicted/explained by X