PHIL150 - Syllogisms

Syllogisms

deductive argument with 3 propositions

Categorical Propositions

something is something; a statement that asserts a relationship between two categories/classes/groups of things

1. two terms: a subject (first) and a predicate (second), which explixitly name classes of things

2. copula: “to be” (is, are, was, were)

3. quantity: universal (all, no) or particular (some = at least one)

4. quality: affirmative or negative (not, no)

Distribution

a feature of the terms in categorical propositions, referring to everything in a given term or only some things

• Subject is distributed if the proposition is universal and undistributed if the proposition is particular

• Predicate is distributed if the proposition is negative and undistributed if the proposition is affirmative.

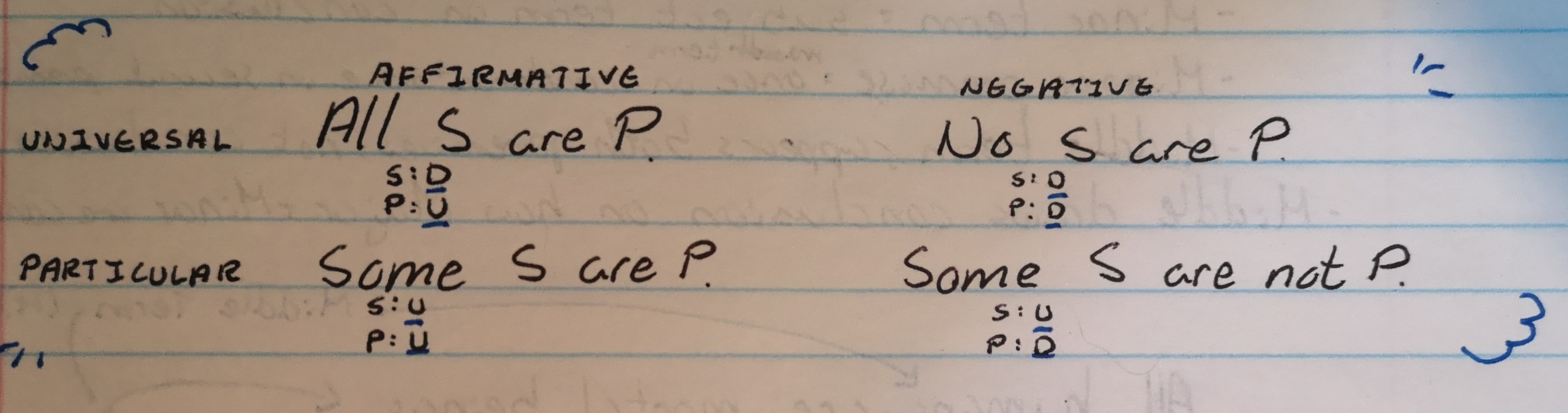
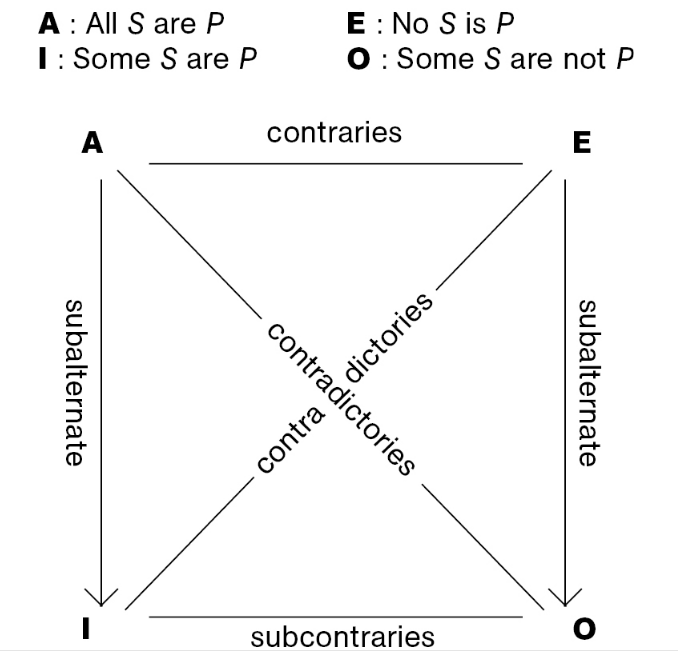
Traditional Square of Opposition

contradictories: they can’t both be false/true; if one is true, the other is false
contraries: can both be false, can’t both be true
subcontraries: can both be true, can’t both be false
subalternates: if the universal is true, the particular is true

existential import

If you have a true claim about a subject, it’s assumed that at least one of the subject actually exists.

If all S are P, conclude some (at least one) S are P, therefore, one S must exist.

Categorical Syllogisms

has 3 categorical propositions, 2 premises, and 1 conclusion,
has a grand total of 3 terms that each only appears twice

Structure of Categorical Syllogisms

Major term (P): predicate term in the conclusion, appears once in conclusion, once in first premise (Major premise)

Minor term (S): subject term in the conclusion, appears once in conclusion, once in second premise (Minor premise)

Middle term (M): appears in both premises, not conclusion, draws conclusion on how major + minor are connected

validity

strength of a deductive argument;
valid when if premises are to be true, then the conclusion is true.
whether an argument is valid depends on what terms are there and where the terms appear in the propositions

any argument with this structure will be valid:
All P are M
No S are M
= No S are P

deductive argument: only works (valid) or doesn’t (invalid), no degree
inductive argument: by degrees (moderately true, etc)
sound argument: valid argument that also has true premises, therefore true conclusion

Rules of Validity

1. Middle term must be distributed at least once

2. If any term is distributed in the conclusion, it must also be distributed in the premise

3. There can’t be two negative premises

4. If the conclusion is negative, a premise must be negative; and if a premise is negative, the conclusion must be negative.