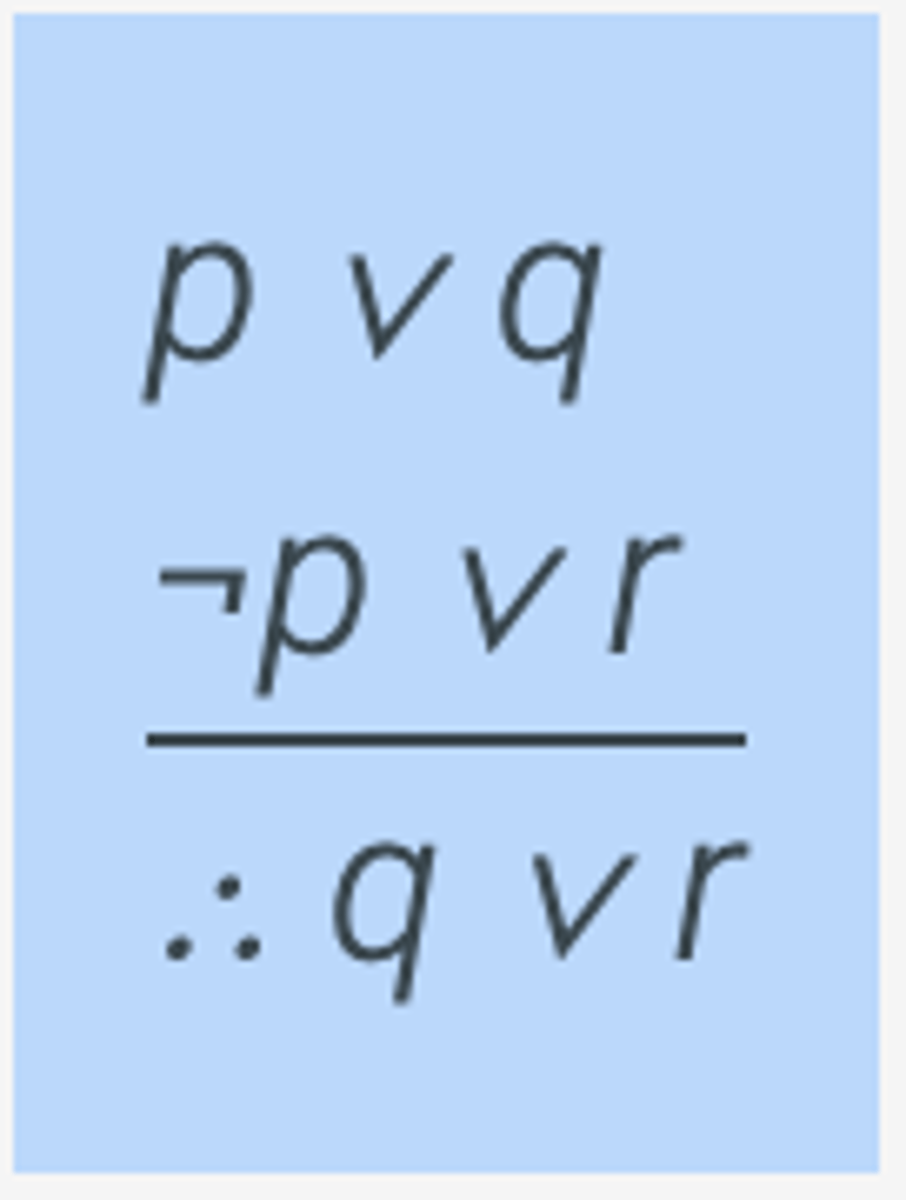C959 Discrete Mathematics I

Conjunction

"and" - symbol ∧ - for conjunction to be true, both sides must be true, think multiplication, 1x1, 0x1, 0x0

Disjunction

"or" - symbol ∨ - for disjunction to be true, one side must be true (said another way, either side can be true). Also true when both sides are true. Only false when both sides are false. This is "inclusive or". Think addition, 0+1, 1+0,

Not

"not" - symbol ¬ - the opposite of the proposition

Inclusive "or"

Inclusive "or" OR - ∨ - means that either side can be true for the proposition to be true AND BOTH sides can be true for the proposition to be true.

2^n

where n is the number of variables, 2^n represents the number of possible outcomes or combinations.

Truth table set up

The first variable should be half of 2^n T's in a row and half 2^n F's in a row. The next variable would be half of the first variable T's in a row (if the first variable had 4 T's in a row, the second variable will have 2 T's in a row), etc and so on until the last variable alternates every time, TFTFTFTF.

exclusive "or"

Exclusive "or" XOR - ⊕ - means that the proposition is ONLY true when either side is true, BUT NOT when both sides are true.

Implication

p → q "Conditional Statement". If p, then q. OR p implies q. However, if hypothesis p is False, it DOES NOT tell us anything about the conclusion q. So, a False hypothesis P will still be True proposition truth value regardless of the Q.

Inverse

Negates the operands. p → q becomes ¬p → ¬q.

Converse

Switches the order of the operands. The converse of p → q is q → p.

Contrapositive

Switches the operands and negates them. p → q becomes ¬q → ¬p. Has the same truth values as p → q.

Bi-conditional

p ⇔ q "p if and only if q" or "p iff q". To be true, both propositions must share the same truth value, ie must be TT or FF.

equivalency

≡

Bi-conditional can also be written as a compound proposition

(p ⇔ q) ≡ (p → q) ∧ (q → p)

compound proposition order of operations

not, and, or, if then, if and only if. Symbols: ¬, ∧, ∨, →, ⇔

∧ propositional operator

and, both propositions must be true for true result or else result is false

¬ propositional operator

not, produces the opposite of the input proposition, true changes to false and vice versa

∨ propositional operator

or, either of the propositions must be true for the result to be true AND if both are true the result is true as well

→ propositional operator

implication p implies q, conditional, if hypothesis is true conclusion must be true, if the hypothesis is false the conclusion is true

↔︎ conditional operator

biconditional, if and only if, iff

propositional order of operations

¬, ∧, ∨, →, ⇔

Hypothesis of a compound proposition

If p, then q. P is the hypothesis, the If proposition

Conclusion of a compound proposition

If p, then q. Q is the conclusion, the Then proposition.

In the words of logic, the only way for a conditional statement to be false is

if the hypothesis is true and the conclusion is false

If the hypothesis is false, then

the conditional statement is true regardless of the truth value of the conclusion.

Translations of p → q

If p, q

q, if p

p implies q

p only if q

p is sufficient for q

q is necessary for p

The proposition p ↔ q is true when p and q _________ and is false _________.

have the same truth value, when p and q have different truth values

tautology

when a compound proposition is always true, p ∨ ¬p

contradiction

when a compound proposition is always false, p ∧ ¬p

logically equivalent

when two compound propositions have the same truth tables regardless of the values of their individual propositions,
¬p ∨ ¬q ≡ ¬(p ∧ q)

De Morgan's law, first version, distributing negation inside a parenthesized expression

¬(p ∨ q) ≡ (¬p ∧ ¬q)

De Morgan's law, second version, distributing negation inside a parenthesized expression

¬(p ∧ q) ≡ (¬p ∨ ¬q)

Idempotent Laws

p ∨ p ≡ p

p ∧ p ≡ p

Associative Laws

( p ∨ q ) ∨ r ≡ p ∨ ( q ∨ r )

( p ∧ q ) ∧ r ≡ p ∧ ( q ∧ r )

arrangement of parentheses does not matter

Commutative Laws

p ∨ q ≡ q ∨ p

p ∧ q ≡ q ∧ p

order does not matter

Distributive Laws

p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r )

p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r )

sign w first variable remains w first variable & sign inside parentheses ends up between sets of parentheses

Identity Laws

p ∨ F ≡ p, where F = False, contradiction

p ∧ T ≡ p, where T = True, tautology

Domination Laws

p ∧ F ≡ F, where F = False, contradiction

p ∨ T ≡ T, where T = True, tautology

Double negation law

¬¬p ≡ p

Complement Laws

p ∧ ¬p ≡ F, ¬T ≡ F, contradiction

p ∨ ¬p ≡ T, ¬F ≡ T, tautology

De Morgan's Laws

¬( p ∨ q ) ≡ ¬p ∧ ¬q

¬( p ∧ q ) ≡ ¬p ∨ ¬q

Absorption Laws

p ∨ (p ∧ q) ≡ p

p ∧ (p ∨ q) ≡ p

Conditional Identities

p → q ≡ ¬p ∨ q

p ⇔ q ≡ ( p → q ) ∧ ( q → p )

Atomic Statement

Can not be divided into smaller statements

Molecular statement

Can be divided into smaller statements

Existential Qualifier

∃ - "there exists" or "there is", true when P(x) is true for a single x in the domain, false when P(x) is false for EVERY x in the domain, ∃xP(x) ≡ P(x1) OR P(x2) ∨ P(x3), etc. Provide counter example when FALSE.

Universal Quantifier

∀ - "for all" or "every", true when P(x) is true for EVERY x in the domain, false when P(x) is false for a single x in the domain, ∀xP(x) ≡ P(x1) AND P(x2) ∧ P(x3), etc. Provide counter example when FALSE.

Base 2 factors

2^0=1(byte), 2^1=2, 2^2=4, 2^3=8(bit), 2^4=16, 2^5=32, 2^6=64, 2^7=128, 2^8=256, 2^9=512, 2^10=1024(KB), 2^11=2048, 2^12=4096, 2^20=1,048,576(MB), 2^30=1,073,741,824(GB), 2^40=1,099,511,627,776(TB), 2^50(PB), 2^60(EB)

Convert base2 to base8 (octal)

Group binary digits into groups of 3 and convert each group to 0-7

Convert base2 to base16 (hexadecimal)

Group binary digits into groups of 4 and convert each group to 0-15 (0-F) (A=10, B=11, C=12, D=13, E=14, F=15

3 parts of predicate logic

1. Variables - x, y, z, these are the subjects of statements
2. Predicates - a property the variable can have
3. Quantifiers - Universal quantifier ∀ (for all), existential quantifier ∃ (there exists)

P(x)

Propositional function, can become a proposition (and have a truth value) when variable is defined or bound by a quantifier.

U

The domain, the universe

Uniqueness Quantifier

∃!x P(x) means that P(x) is true for one and only one x in the universe of discourse.

DeMorgan's Laws for Quantifiers

¬∀x P(x) ≡ ∃x ¬ P(x)
¬∃x Q(x) ≡ ∀x ¬ Q(x)

Quantifiers (∀, ∃, ∃!) are applied ...

before logical operators

A variable in the predicate, P(x) is called a

free variable, it is not bound

The variable in the statement ∀x P(x) is called a

bound variable, because it is bound by the quantifier

∀x∀y M(x,y)

For every pair of x and y, M(x,y) is true

∃x∃y M(x,y)

There exists at least one pari of x and y such that M(x,y) is true

∃x∀y M(x,y)

There exists at least one x that pairs with ALL y, such that M(x,y) is true

∀x∃y M(x,y

For each x, there is at least one y, such that M(x,y) is true

¬∀x ∀y P(x, y) ≡

∃x ∃y ¬P(x, y), De Morgan's law w nested quantifiers

¬∀x ∃y P(x, y) ≡

∃x ∀y ¬P(x, y), De Morgan's law w nested quantifiers

¬∃x ∀y P(x, y) ≡

∀x ∃y ¬P(x, y), De Morgan's law w nested quantifiers

¬∃x ∃y P(x, y) ≡

∀x ∀y ¬P(x, y), De Morgan's law w nested quantifiers

A proposition is true or false whereas an argument is ...

valid or invalid

An argument is valid if all the premises are true AND ...

the conclusion is true. It is invalid otherwise.

Modus Ponens

((p -> q) ∧ p) -> q

Modus Tollens

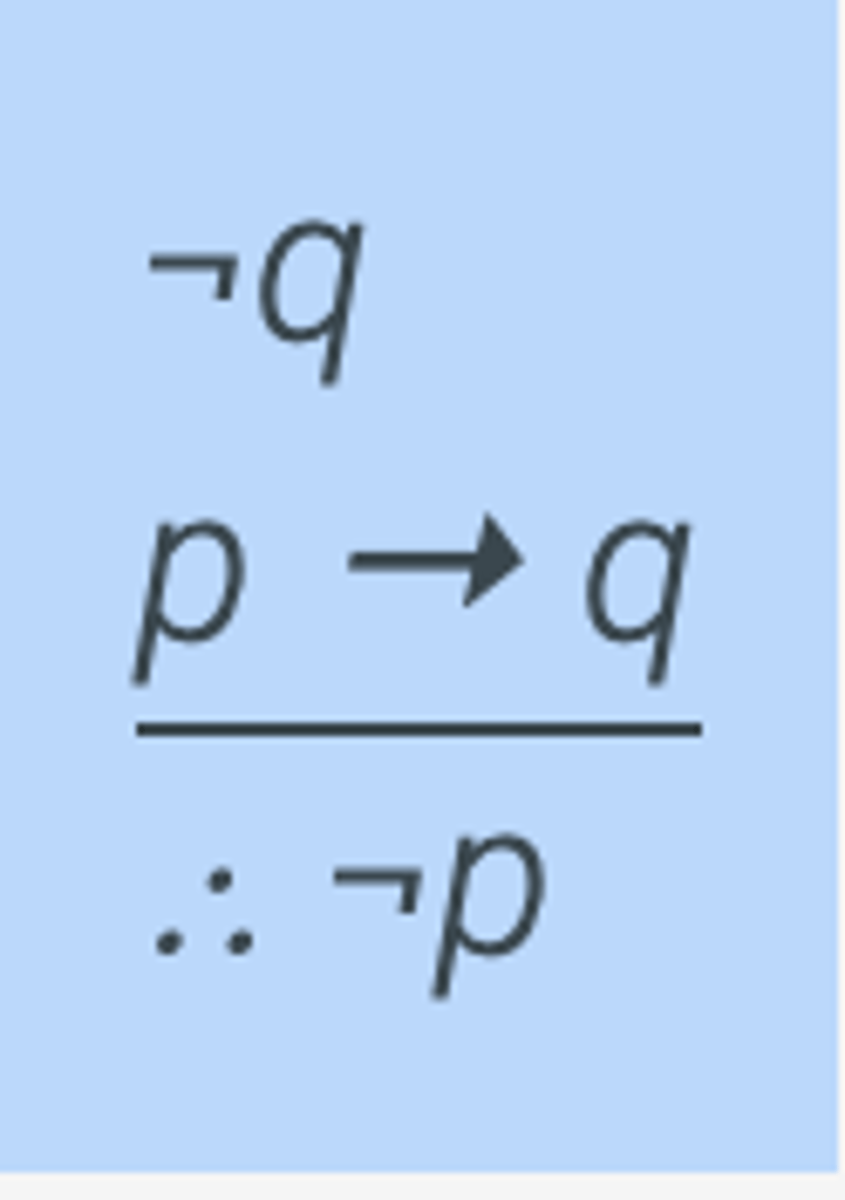
Addition

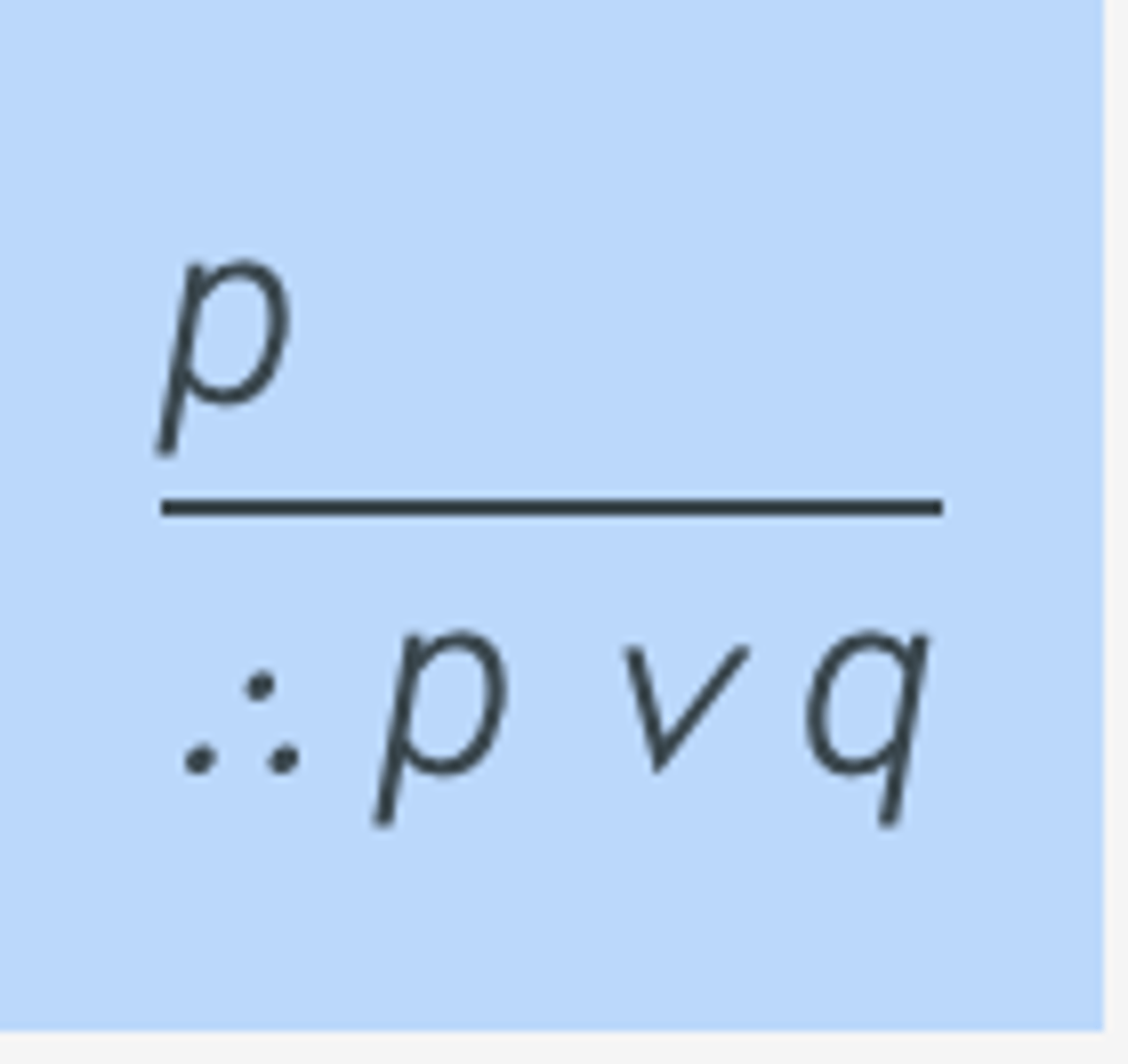
Simplification

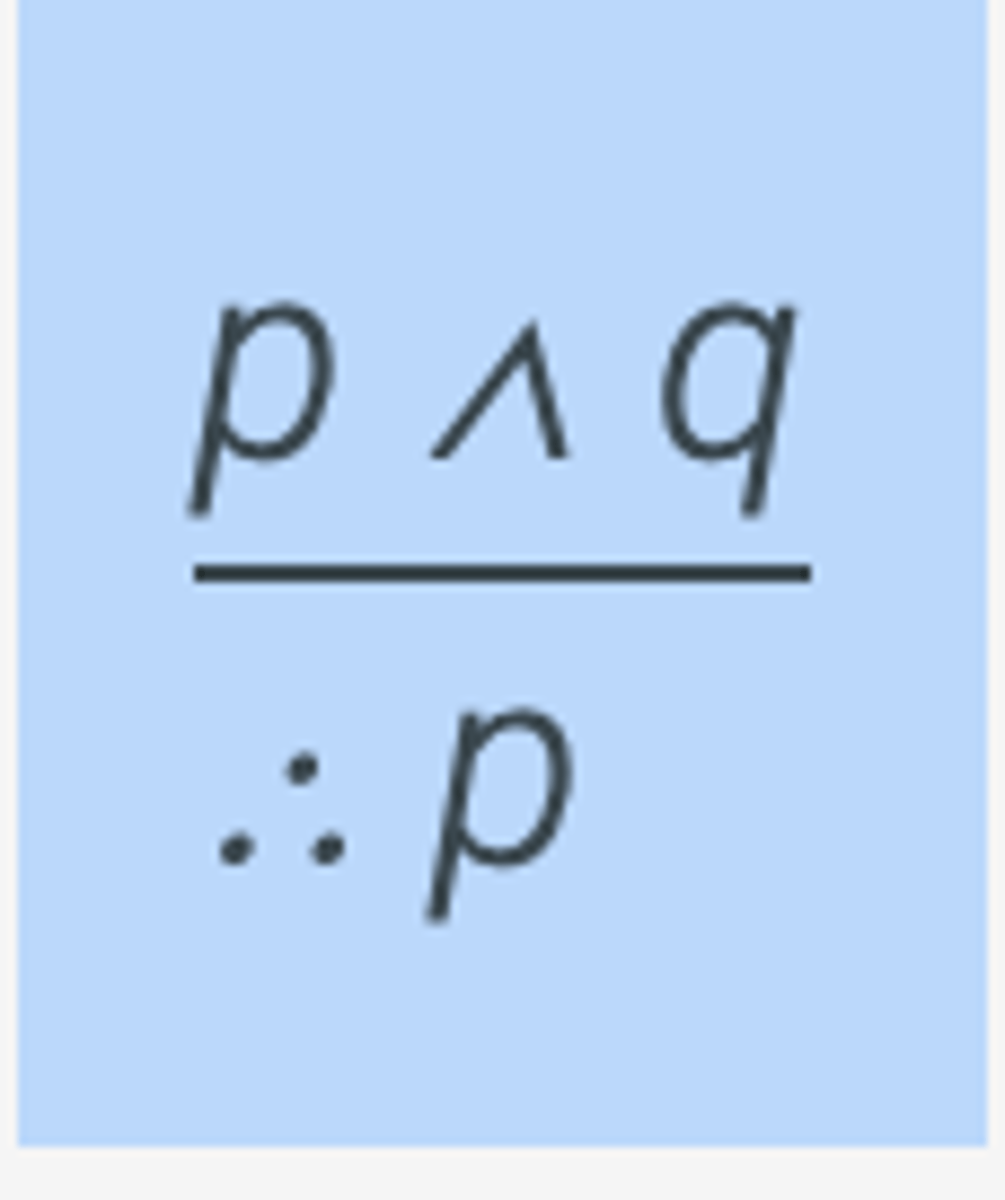
Conjunction

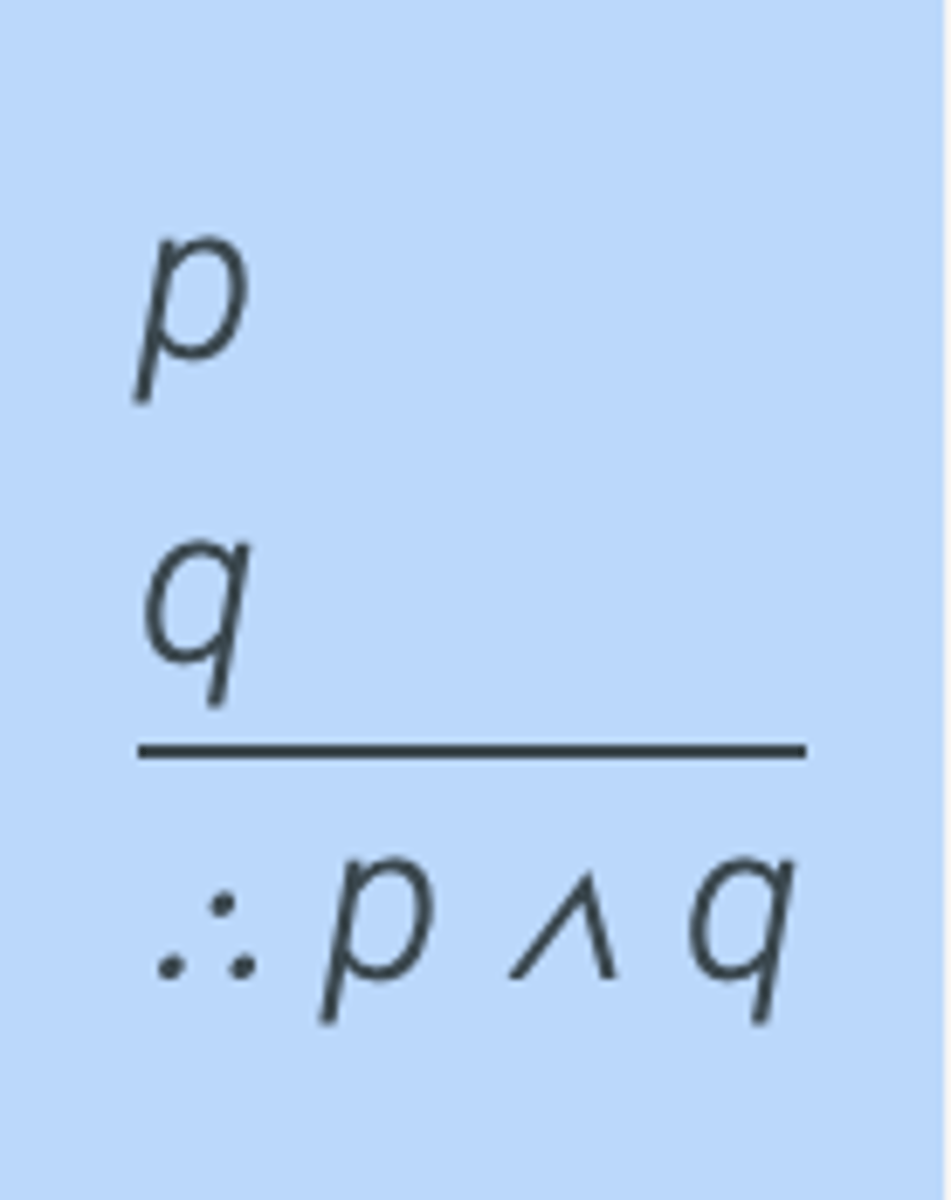
Hypothetical Syllogism

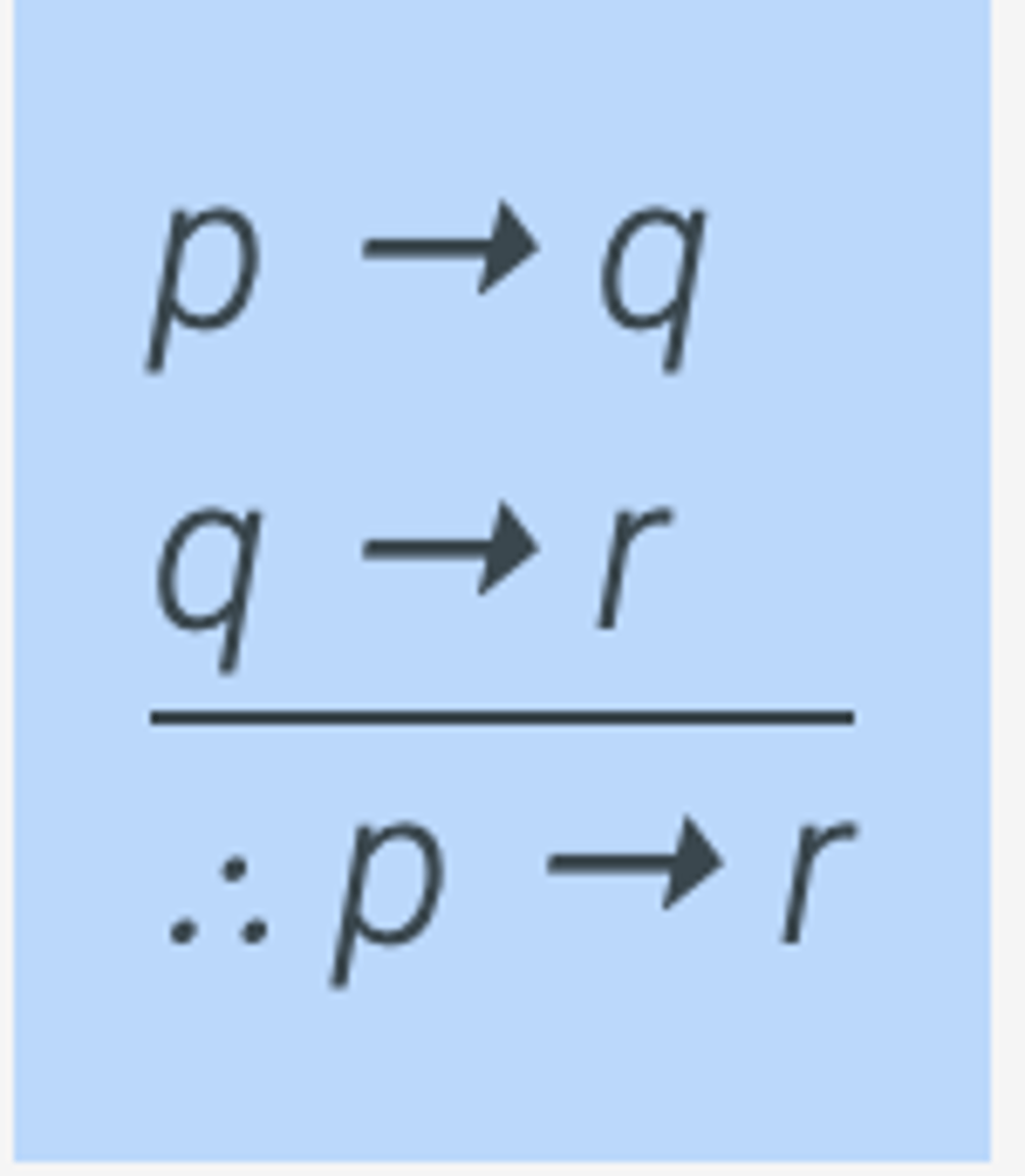
Disjunctive Syllogism

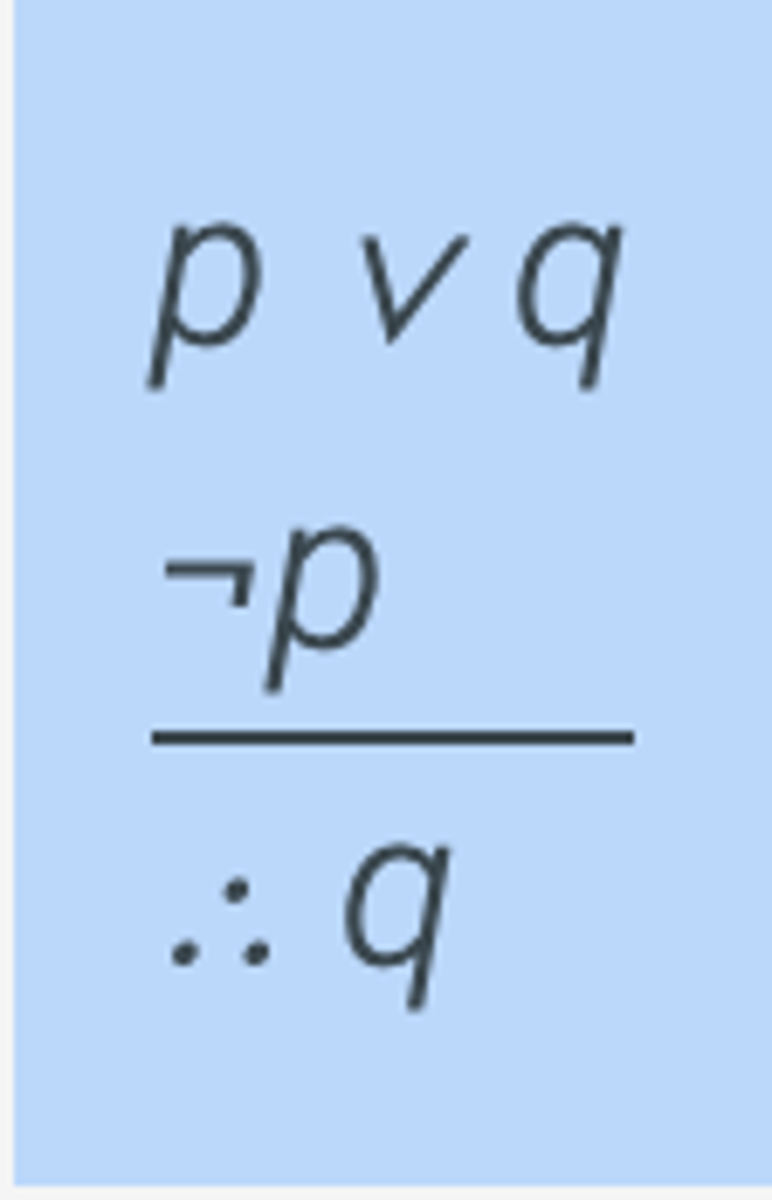
Resolution