Embedded Systems 1 - Flowcharts/Pseudocode & Numbers/Math

What are the advantages of flowcharts & pseudocode?

- validating algorithm & steps

- determining key functions

- dividing up larger complex into smaller jobs

- segregate programs for design teams

- communication tool between stakeholders

What are flowcharts and pseudocode for?

methods to provide structure to a program

Flowchart/ Pseudocode Characteristics - Representation

Flowchart - symbolic, pseudocode - natural text

Flowchart/ Pseudocode Characteristics - Detail

Flowchart - too much detail = bad, Pseudocode - flexible

Flowchart/ Pseudocode Characteristics - Modification

Flowchart - hard to modify for large/complex implementations, Pseudocode - easy

Flowchart/ Pseudocode Characteristics - Structure

Flowchart - specific structure, symbols, Pseudocode is open-world

Flowchart/ Pseudocode Characteristics - Understanding

Flowchart --> easy to understand

Pseudocode --> more complex to understand

When is it better to use flowcharts instead of pseudocode?

smaller code jobs

When is it better to use pseudocode instead of flowcharts?

larger code jobs

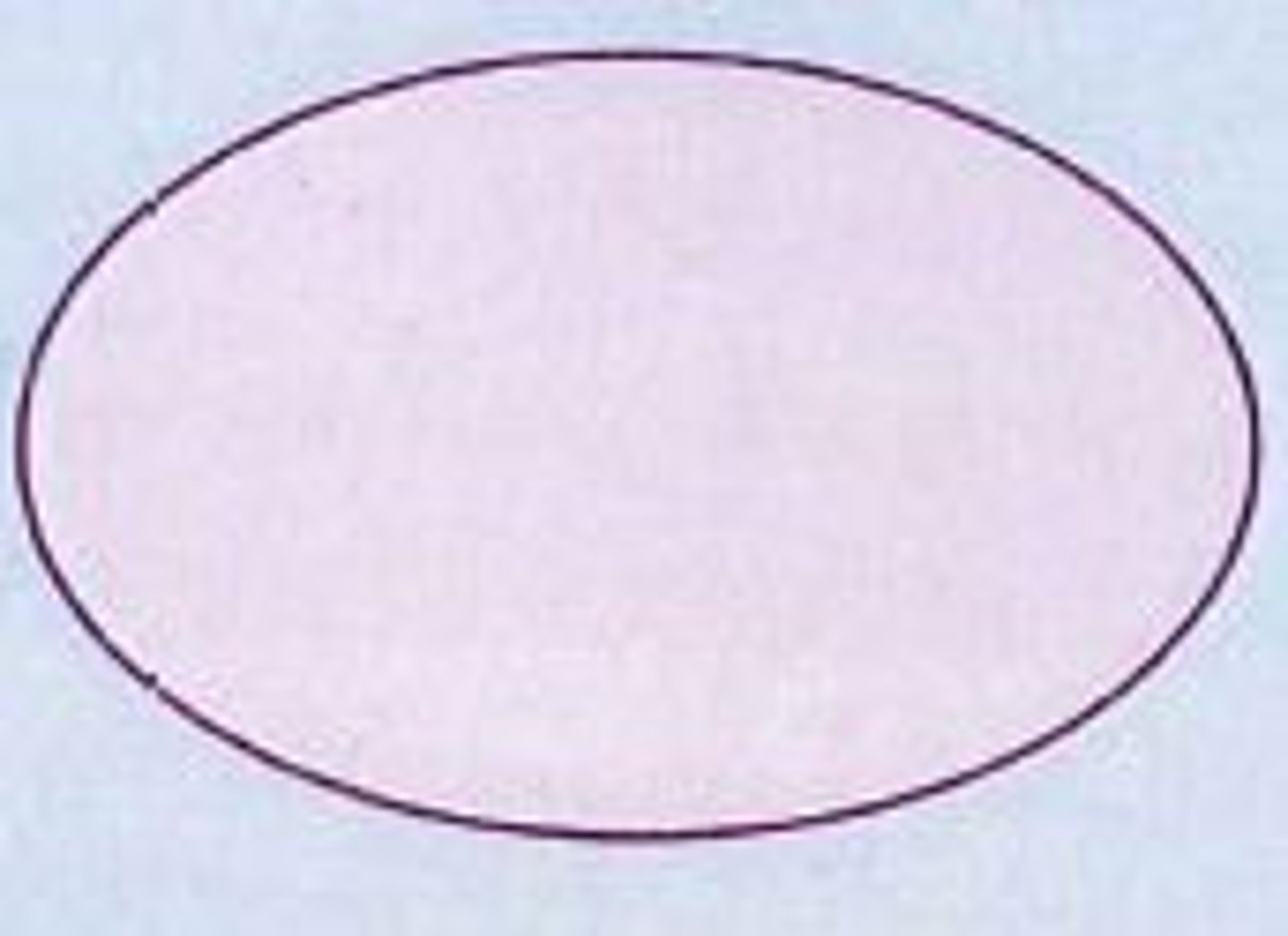
Flowchart symbol - Start/end

hotdog shape (long oval)

flowchart symbol - input/output

parallelogram

flowchart symbol - process

rectangle

flowchart symbol - decision/condition

diamond

flowchart symbol - delay

AND symbol [check slide 4]

In summary, flowcharts:

useful for planning stages or showing code graphically

In summary, pseudocode:

morphs along with code, mergeable to real code, but linear and does not give overall visual description

Convert #0b1011 to base 10

= 12^0 + 12^1 + 0 + 1*2^3 = 8 + 2 + 1 = 11

Base 16 (Hex) Digits

0-9, A= 10, B = 11, C=12, D=13, E=14, F=15

Convert 0xFE32 to decimal (base 10)

65044

Adding hex numbers: 0x0A + 0x08

0x12 = 18 (base 10)

Adding hex numbers

the same as decimal, except carry 16 instead of 10

Convert 0b110111 to decimal

55

Convert 170 to binary

0b10101010 (procedure: keep dividing by 2, first remainder is LSB, last remainder is MSB)

Convert 0b110101110010 to Hex and then to decimal

Hex = 0xD72

Decimal = 3442

Convert 65430 to Hex then to binary

Hex = 0xFF96 (keep dividing by 16 - procedure)

Binary = 0b1111 1111 1001 0110

Convert $ABCDEF to decimal

hex --> decimal

11,259,375

Convert %1010110 to decimal

86

Convert 120 decimal to binary

1111000

Convert %110101010010 to Hex then to decimal

Hex = 0xD52

Decimal = 3410

Convert 35210 to Hex then to binary

Hex = 0x898A

Binary = 0b00110101001000010000

Convert $AFCABE to decimal:

11,520,702

Convert $E4CFEA to binary:

9223372036854775807

Given n bits, how many values can you encode?

2^n -1

Byte

8 bits

Nibble

4 bits

kilobit (Kb)

2^10 bits = 1024 bits

kilobyte (KB)

2^10 bytes = 8192 bits

megabyte (MB)

2^20 bytes = 2^23 bits

Binary arithmetic - adding

Logically, adding is the XOR function per column, can also convert to decimal and add

0+0 = 0

1+0 = 1

0+ 1 = 1

1+1 = 10 (2)

Signed Numbers

- use MSB as the "sign" bit

0 = positive

1 = negative

- can think of subtractions as adds with a negative number

Signed Numbers 2's Complement (Represent a negative number as twos complement in binary)

Steps

1) Take the positive binary (MSB = 0)

2) Invert all bits

3) Add 1

Signed Numbers 2's Complement (twos complement --> negative number)

Steps

1) take twos complement number

2) subtract 1

3) invert all bits

ex) these steps give binary equal to 5, so you know the negative number is -5

2's complement range

8 bits: -128 to 127

general: (2^n-1)-1 positive numbers to 2^n-1 negative numbers, and the number 0

Twos complement: 8-3 = 8 + -3

0000 1000 (8)

1 1 1 1 1 101 (-3)

-----------------

0000 0101 (5)

Twos complement: 8-9 = 8+-9

0000 1000 (8)

1111 0111 (-9)

----------------

1111 1111 --> MSB is 1, so do reverse to find negative number (-1)

22+7 in binary, state if valid for signed and unsigned

00011101, valid for both

22-7 in binary, state if valid for signed and unsigned

00001111, valid for both

-22-7 in binary, state if valid for signed and unsigned

11100011, valid for signed only

-22+7 in binary, state if valid for signed and unsigned

11110001, valid for signed only

Before you start a math operation what two things must you know?

1) signed or unsigned

2) number of bits (8, 16, 32 etc)