P5 - Forces

Scalar quantities only have what?

Magnitude only.

Vector quantities have what?

Magnitude and an associated direction.

What may a vector quantity be represented by?

An arrow.

What does the length of the arrow in a vector quantity represent?

Magnitude.

What is a force?

A push or pull that acts on an object due to the interaction with another object.

All forces between objects are either what or what?

Contact forces or non-contact forces.

What is a contact force?

The objects are physically touching.

What is a non-contact force?

The objects are physically separated.

What are examples of contact forces?

•Friction

•Air resistance

•Tension

•Normal contact force.

What are examples of non-contact forces?

•Gravitational force

•Electrostatic force

•Magnetic force.

What type of quantity is force?

A vector quantity.

Students should be able to describe the interaction between pairs of objects which produce a force on each object. The forces to be represented as vectors.

.

What is weight?

The force acting on an object due to gravity.

Why is the force of gravity close to the Earth there?

Due to the gravitational field around the Earth.

What does the weight of an object depend on?

The gravitational field strength at the point where the object is.

What is the equation used to calculate the weight of an object, including the units?

weight=mass×gravitational field strength

[W=mg]

weight, W , in newtons, N

mass, m , in kilograms, kg

gravitational field strength, g , in newtons per kilogram, N/kg

What is the name of the single point where the weight of an object may be considered to act at?

Centre of mass.

What is the relationship between the weight of an object and the mass of an object?

Directly proportional (∝).

How is weight measured?

A calibrated spring-balance (a newtonmeter).

What is a resultant force?

A number of forces acting on an object replaced by a single force that has the same effect as all the original forces acting together.

Students should be able to calculate the resultant of two forces that act in a straight line.

.

Students should be able to:

describe examples of the forces acting on an isolated object or system

use free body diagrams to describe qualitatively examples where several forces lead to a resultant force on an object, including balanced forces when the resultant force is zero.

.

How can a single force be resolved?

Into two components acting at right angles to each other.

What effect do the two component forces have together?

The same effect as the single force.

Students should be able to use vector diagrams to illustrate resolution of forces, equilibrium situations and determine the resultant of two forces, to include both magnitude and direction (scale drawings only).

.

What happens when a force causes an object to move through a distance?

Work is done on the object.

A force does work on an object when the force causes a __________________ of the object.

Displacement.

What is the equation used to calculate the work done by a force on an object, including the units?

work done=force×distance (moved along the line of action of the force)

[W=Fs]

work done, W , in joules, J

force, F , in newtons, N

distance, s , in metres

1 joule is equal to what?

1 newton-metre.

Students should be able to convert between newton-metres and joules.

.

What does the work done against the frictional forces acting on an object cause?

A rise in the temperature of the object.

Students should be able to:

give examples of the forces involved in stretching, bending or compressing an object

explain why, to change the shape of an object (by stretching, bending or compressing), more than one force has to be applied - this is limited to stationary objects only

describe the difference between elastic deformation and inelastic deformation caused by stretching forces.

.

What is the equation used to calculate the force of a spring, including the units?

force=spring constant×extension

[F=ke]

force, F , in newtons, N

spring constant, k , in newtons per metre, N/m

extension, e , in metres, m

What is the relationship he extension of an elastic object, such as a spring, and the force applied?

Directly proportional (∝), provided that the limit of proportionality is not exceeded.

What does this relationship also apply to (F=ke)?

The compression of an elastic object, where 'e' would be the compression of the object.

A force that stretches (or compresses) a spring does what?

Work.

What type of energy is stored in the spring?

Elastic potential energy.

Provided the spring is not inelastically deformed, the work done on the spring and the elastic potential energy stored are what?

Equal.

Students should be able to:

describe the difference between a linear and non-linear relationship between force and extension

calculate a spring constant in linear cases

interpret data from an investigation of the relationship between force and extension

.

What is the equation used to calculate work done in stretching (or compressing) a spring (up to the limit of proportionality), including the units?

elastic potential energy=0.5×spring constant ×(extension)²

[Ee=½ke²]

elastic potential energy, Ee, in joules, J

spring constant, k , in newtons per metre, N/m

extension, e , in metres, m

Students should be able to calculate relevant values of stored energy and energy transfers.

.

What is distance?

How far an object moves.

What does distance not involve?

Direction.

What type of quantity is distance?

Scalar.

What does displacement include?

Both the distance an object moves, measured in a straight line from the start point to the finish point, and the direction of that straight line.

What type of quantity is displacement?

Vector.

Students should be able to express a displacement in terms of both the magnitude and direction.

.

MS 1, 3c

Throughout this section (Forces and motion) , students should be able to use ratios and proportional reasoning to convert units and to compute rates.

.

What does speed NOT involve?

Direction.

What type of quantity is speed?

Scalar.

The speed of a moving object is rarely what?

Constant.

When people walk, run or travel in a car, their speed is constantly what?

Changing.

What does the speed at which a person can walk, run or cycle depend on?

Many factors:

•Age

•Terrain

•Fitness

•Distance travelled.

What are the typical values of walking, running and cycling?

•walking ̴ 1.5 m/s

•running ̴ 3 m/s

•cycling ̴ 6 m/s.

Students should be able to recall typical values of speed for a person walking, running and cycling as well as the typical values of speed for different types of transportation systems.

.

True or false: It is not only moving objects that have varying speed.

True - It is not only moving objects that have varying speed.

True or false: The speed of sound and the speed of the wind don't vary.

False - The speed of sound and the speed of the wind also vary.

What is the typical value for the speed of sound in air?

330 m/s.

Students should be able to make measurements of distance and time and then calculate speed s of objects .

.

What is the equation used to calculate the distance travelled in a specific time for an object moving at constant speed, including units?

distance travelled=speed×time

[s=vt⁢]

distance, s , in metres, m

speed, v , in metres per second, m/s

time, t , in seconds, s

Students should be able to calculate average speed for non-uniform motion.

.

What is the velocity of an object?

Its speed in a given direction.

What type of quantity is velocity?

Vector.

Students should be able to explain qualitatively, with examples, that motion in a circle involves constant speed but changing velocity .

.

If an object moves along a straight line, how can the distance travelled can be represented?

A distance-time graph.

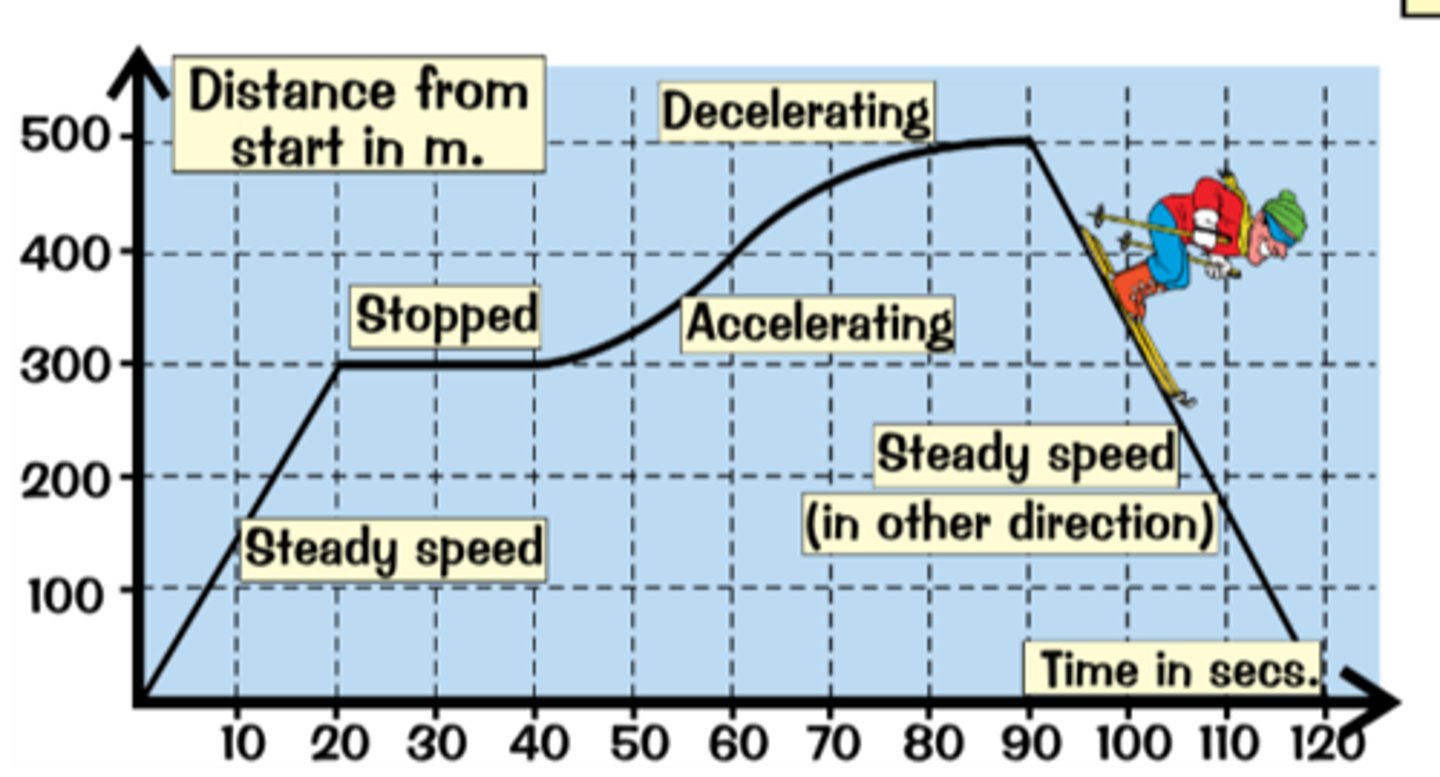
How can the speed of an object be calculated from its distance-time graph?

The gradient of its distance-time graph.

How can the speed, at any particular time, of an accelerating object be determined?

By drawing a tangent and measuring the gradient of the distance-time graph at that time.

Students should be able to draw distance-time graphs from measurements and extract and interpret lines and slopes of distance-time graphs, translating information between graphical and numerical form.

.

Students should be able to determine speed from a distance-time graph.

.

What is the equation used to calculate the average acceleration of an object, including the units?

acceleration=change in velocity/time taken

[a=∆vt⁢] [a=v-u/time]

acceleration, a , in metres per second squared, m/s2

change in velocity, ∆v , in metres per second, m/s

time, t , in seconds, s

What is deceleration?

An object slowing down.

Students should be able to estimate the magnitude of everyday accelerations.

.

How can the acceleration of an object can be calculated?

The gradient of a velocity-time graph.

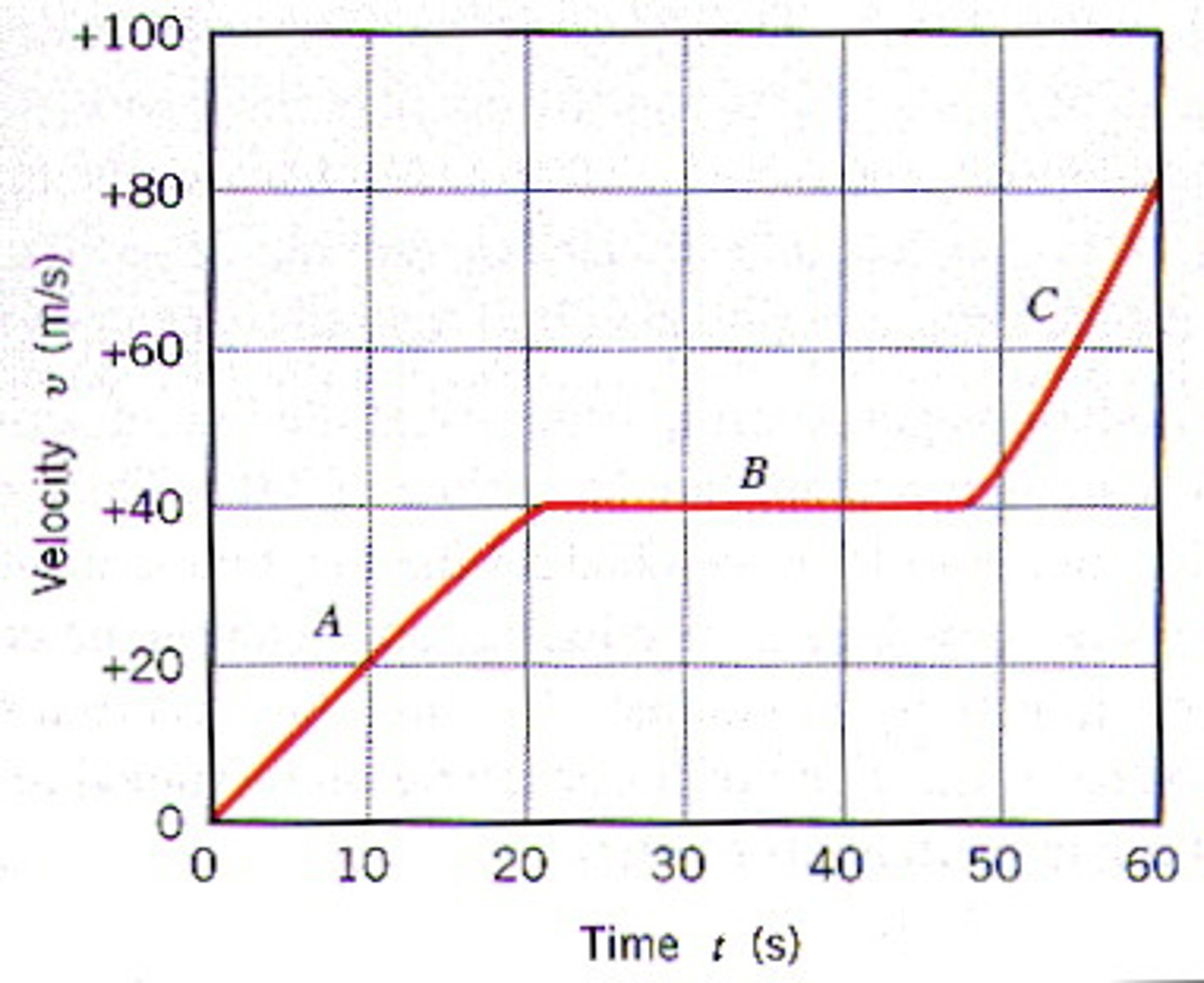
How can the distance travelled by an object (or displacement of an object) be calculated?

From the area under a velocity-time graph.

Students should be able to:

draw velocity-time graphs from measurements and interpret lines and slopes to determine acceleration

(HT only) interpret enclosed areas in velocity-time graphs to determine distance travelled (or displacement)

(HT only) measure, when appropriate, the area under a velocity-time graph by counting squares.

.

What is the equation that applies to uniform acceleration, including the units?

2×acceleration×distance=(final velocity)²-(initial velocity)²

[2as=v²-u²]

final velocity, v , in metres per second, m/s

initial velocity, u , in metres per second, m/s

acceleration, a , in metres per second squared, m/s²

distance, s , in metres, m

What is the acceleration for any object falling freely under gravity near the Earth's surface?

9.8 m/s².

An object falling through a fluid initially accelerates due to what?

The force of gravity.

Eventually the resultant force (of an object falling and accelerating) will be zero and the object will move at its what?

Terminal velocity.

What is Newton's First Law?

If the resultant force acting on an object is zero and:

•the object is stationary, the object remains stationary

•the object is moving, the object continues to move at the same speed and in the same direction. So the object continues to move at the same velocity.

When a vehicle travels at a steady speed, the resistive forces balance the what?

Driving force.

The velocity (speed and/or direction) of an object will only change if what?

A resultant force is acting on the object.

Students should be able to apply Newton's First Law to explain the motion of objects moving with a uniform velocity and objects where the speed and/or direction changes.

.

What is inertia?

The tendency of objects to continue in their state of rest or of uniform motion.

What is Newton's Second Law?

The acceleration of an object is proportional to the resultant force acting on the object, and inversely proportional to the mass of the object.

What is the equation for Newton's Second Law, including the units?

resultant force=mass×acceleration

F=ma

force, F , in newtons, N

mass, m , in kilograms, kg

acceleration, a , in metres per second squared, m/s²

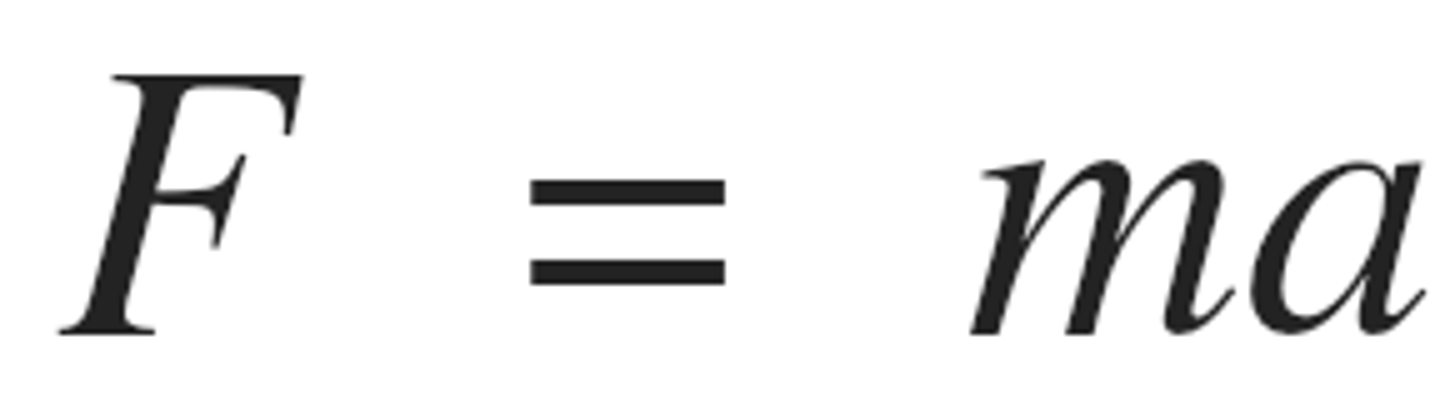
Students should be able to explain that:

inertial mass is a measure of how difficult it is to change the velocity of an object

inertial mass is defined as the ratio of force over acceleration .

.

Students should be able to estimate the speed, accelerations and forces involved in large accelerations for everyday road transport.

Students should recognise and be able to use the symbol that indicates an approximate value or approximate answer, ̴

.

What is Newton's Third Law?

Whenever two objects interact, the forces they exert on each other are equal and opposite.

Students should be able to apply Newton's Third Law to examples of equilibrium situations.

.

What is the stopping distance of a vehicle?

The sum of the distance the vehicle travels during the driver's reaction time (thinking distance) and the distance it travels under the braking force (braking distance).

Stopping distance = Thinking distance + Braking distance

For a given braking force the greater the speed of the vehicle, the greater the what?

Stopping distance.

True or false: Reaction times vary from person to person.

True - reaction times vary from person to person.

What are the typical values for a person's reaction time?

Range from 0.2s to 0.9s.

What are the factors which can affect a driver's reaction time?

•Tiredness

•Drugs

•Alcohol

•Distractions

Students should be able to:

explain methods used to measure human reaction times and recall typical results

interpret and evaluate measurements from simple methods to measure the different reaction times of students

evaluate the effect of various factors on thinking distance based on given data.

Measure the effect of distractions on reaction time.

How can the braking distance of a vehicle be affected?

Adverse road and weather conditions and poor condition of the vehicle.

What are examples of adverse road conditions?

Wet or icy conditions.

What is the poor condition of the vehicle limited to?

The vehicle's brakes or tyres.

Students should be able to:

explain the factors which affect the distance required for road transport vehicles to come to rest in emergencies, and the implications for safety

estimate how the distance required for road vehicles to stop in an emergency varies over a range of typical speeds.

.