Light and Special Relativity
1/25
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
26 Terms
Inertial vs non-inertial frames of reference
A frame of reference - the perspective from which the motion of objects is observed and/or measured
Inertial frame of reference (FOR) – a non-accelerating frame of reference | Non-inertial FOR – an accelerating frame of reference |
Example: A camera fixed to the ground is stationary and thus will capture a video from an inertial frame of reference. | Example: A camera falling down will capture a video from a non-inertial frame of reference since the camera itself is experiencing gravitational acceleration. |
|
|
Pendulum Experiment
Experiment used to tell if you are inside an inertial or non-inertial frame of reference

The Special Theory of Relativity
Published by Einstein in 1905
Postulate | 1st postulate | 2nd postulate |
Description | The laws of physics are the same in all inertial frames of reference (Galilean principle of relativity) | The speed of light in vacuum has the same value for all observers, regardless of the state of motion of the observer or the source |
Impact |
|
|
Galileo’s Principle of Relativity
Prosed by Galileo in 1632
The mechanical laws of physics are the same for every inertial observer
Results of any experiment will be identical
There is no way to differentiate between a frame moving at constant speed and a frame at rest
Cannot be done without consulting another FOR (e.g. looking outside the window to see movement, feeling wind on your face, looking at a satellite)
→ e.g. If I am inside a boat, and I cannot look outside or feel the waves rocking, I cannot tell whether I am moving with a constant velocity or stationary
Means all inertial frames of reference are equivalent
It is possible to determine that one frame is moving relative to another, but it is impossible to determine which of them is at rest
There is no absolute stationary
Velocity is always defined relative to some external point
E.g. Our car’s velocities are measured relative to the Earth
Historical context about the Relative Speed of Light
Throughout history Light’s speed was calculated to be 3x108m/s
People wanted to know what speed this was measured relative to
People assumed light required a medium to travel through, like other waves
Huygen thought light was a longitudinal wave that travelled through perfectly elastic particles that fill up space (the aether)
Maxwell showed light was EM, but they still didn’t know what medium it needed to propagate in
In the 19th century, scientists did experiments to determine what medium light needed to travel in
It was proposed that the aether had an absolute frame of reference
∴ Light waves had a fixed velocity relative to the aether
The aether theory was not backed up by experimental evidence
E.g. Michelson-Morley experiment tried to find how light’s speed changed relative to earth, but had no results proving that light’s speed changed
Einstein’s thought experiment for the relative speed of light
“Suppose I am sitting in a train travelling at the speed of light. If I hole a mirror in front of me, will I see my reflection?”
Possible answer 1: No
If the train was travelling at the speed of light, the photons reflected from his face would not reach the mirror in order to be reflected back
Since he cannot see his own reflection in the mirror, he would know the train was travelling at a constant speed (c), without consulting an external frame of reference
This violates the principle of relativity as an observer can detect their motion despite being in an inertial frame of reference
Possible answer 2: Yes
This means that light would travel at its normal speed relative to the train, and he could see his reflection
This does not violate the principle of relativity as he would not know whether he is moving or at rest in the train
However, based on the addition of velocities, the light inside the train would be travelling twice its original speed (2c) for a stationary observer outside the train
This is impossible because nothing can travel faster than the speed of light (c), even light itself
Einstein concluded that the principle of relativity cannot be violated ∴ he can see his reflection.
Resolved this issue by stating that the speed of light is the same for any observer
Since: speed = distance ÷ time, the stationary observer and the moving observer must perceive distance and time differently → ratio changes but speed stays the same
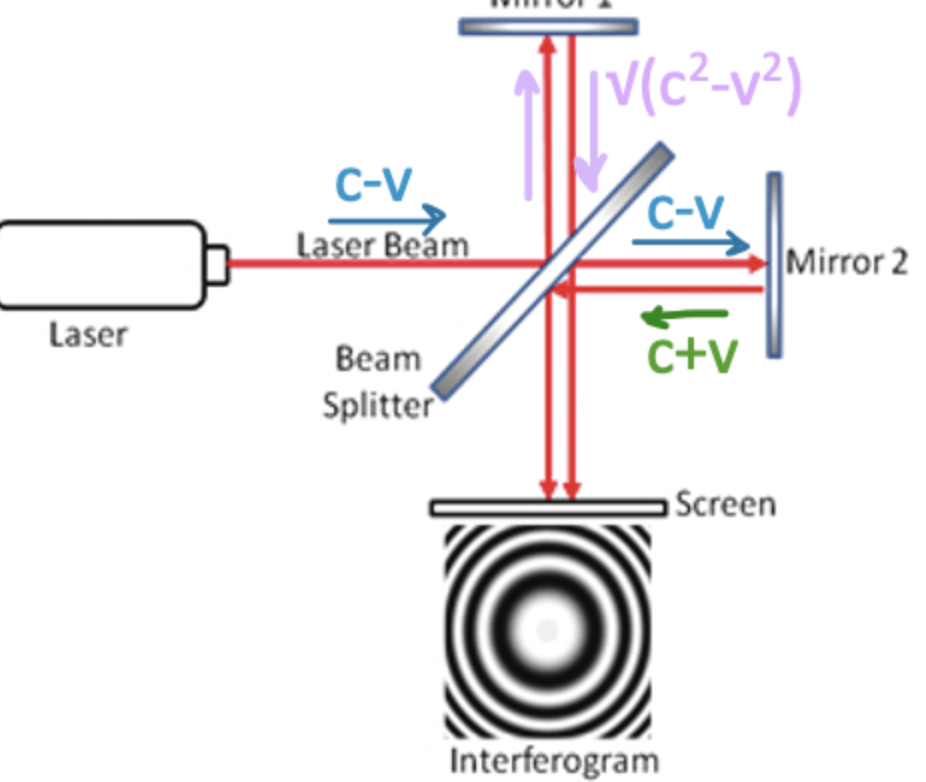
Michelson-Morely Experiment: purpose and result
Purpose of Experiment: to measure the velocity of the earth through the aether
By measuring the difference in the speed of light relative to the earth due to the Earth’s motion relative to the aether (called the aether wind)
Scientists used Newtonian relative motion to theorise that Earth's movement through the aether → caused the aether wind
Results of Experiment
When the interferometer was rotated, there was no change in the interference pattern observed → NULL RESULT
Disproved the existence of the aether wind
This supported Einstein’s theory that the speed of light is constant in all reference frames
Michelson-Morely Experiment: method
Method of Experiment
Directed a beam of light at an angle of 45° to a beam splitter (half-silvered, half transparent mirror)
The beam splitter splits the beam by allowing half of it to pass through and the other half to be reflected
They used a Michelson interferometer (an optical instrument that splits a light beam into two paths, reflects them back, and then recombines them to create an interference pattern)
The reflected light travelled to meet mirror 1, then was reflected back onto the beam splitter and into the detector
The light that passed through the beam splitter travelled to meet mirror 2, then was reflected back onto the beam splitter and into the detector
When these light beams meet at the detector, they interfere to create interference fringes
The interferometer is rotated by 90° and the interference pattern is monitored during the rotation
The rotation would cause the speed of light in each arm to change due to the changing direction of velocity relative to the aether wind
The speed of light changing means that the two beams would arrive at the detector at different times, and their relative phase would be different
This would change the interference pattern during rotation
Time Dilation
the difference in elapsed time between two clocks that are in motion relative to each other
Observers in different inertial frames will measure different time intervals between a pair of events
A moving clock runs slower than an identical stationary clock
More second’s pass on a stationary clock than a moving clock according to your perspective
The faster a thing moves relative to the observer, the slower it looks from a “stationary” observer
Thought exp for time dilation equation
Light must travel further for the observer outside than for the observer inside the train
According to the 2nd postulate of Special Relativity, the speed of light is the same for both observers
Since light travels a further distance for the observer outside the train, they measure a longer time than for the observer inside the train
Hence, the observer’s clock inside the train runs slow compared to the observer outside

Proper vs Dilated time
Proper Time | Dilated Time |
· The shortest time possible for the event · Event occurs at the same special location · The observer is stationary relative to the event (the event happens in front of you) → same FOR · One clock needed to measure | · Longer time · Events occur at different spatial locations · The observer sees the event moving → different FORs · Two clocks (one at each event) needed to measure time |
Length Contraction
the difference in lengths of an object measured by two observers that are in relative motion compared to each other
The length will be shorter if the object is moving relative to the observer making the measurement
The observer at rest with respect to the object measured is the proper length
The observer moving with a relative speed will observe a shorter length
Only contracts in the same plane as the movement
Example: Ball only experiences length contraction in the horizontal dimension (not vertical) since that is the direction of velocity
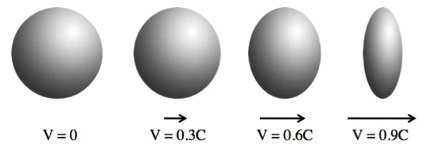
Proper vs Contracted length
Proper Length | Contracted Length |
· The largest length possible · If the object is stationary relative to the observer measuring it → Same FOR · Seen in one spatial location · No relative velocity between measurer and object | · Shorter length · If the object is moving with a constant speed relative to the observer → different FORs · Seen in more than one spatial location |
Thought exp for Length Contraction equation

Limitation of Special Relativity
These effects are negligible when a frame of reference is not moving at a relativistic speed.
Relativistic effects can occur in non-inertial frames of reference but in these scenarios, they are not only attributed to special relativity. Effects due to general relativity must be considered in non-inertial frames of reference. As a result, only relativistic effects in inertial frames of reference are entirely due to special relativity.
Evidence for Time Dilation and Length Contraction: Muons
Muons – unstable elementary particle
Have a charge equal to an electron
Have a mass 207 times larger than an electron
Produced by the absorption of cosmic radiation in the high atmosphere
Have an average lifetime of 2.2 𝜇s when measured in a FOR at rest with respect to them
They decay to produce energy and other particles
Speed is around 0.998c
According to classical physics: could only travel a distance of 600m before they decay ∴ most should not reach earth
However, lots of muons are detected on earth due to time dilation and length contraction
FOR | Time taken for muon to fall | Length of fall |
Muon | Proper time | Contracted length |
Observer on earth | Dilated time | Proper length |
Evidence for Time Dilation and Length Contraction: particle accelerators
Lithium Ions
In 2014, an experiment was conducted to demonstrate time dilation using lithium ions travelling at 0.338c in a particle accelerator.
The time interval between excitation of electrons in lithium ions and their return to ground state was measured when lithium ions are travelling at 0.338c and at rest.
Physicists found that the interval was longer for moving lithium ions compared to those at rest, as measured by a stationary observer in the laboratory.
This difference in time was consistent with time dilation.
Increased lifetimes of short-lived particles
Unstable particles (like muons) are produced travelling at high speeds
Due to high speed of these particles, their lifetime is observed to be longer in the Earth’s frame of reference → we measure dilated times
Evidence for Time Dilation and Length Contraction: atomic clocks
Hafele-Keating Experiment
Involved flying atomic clocks on aeroplanes to directly measure time dilation
One clock left on the ground at Washington DC
One clock was flown around the world eastwards (same direction of earth’s spin)
One clock was flown around the world westwards (opposite direction of earth’s spin)
Once all the clocks returned to earth, the times were compared
The time on each clock was different due to the different amounts of time dilation
Atomic clocks have very high precision → needed to even the smallest amounts of time dilation
Experiments agreed with predictions of relativity
Mass Dilation
mass of an object appears to increase as its speed approaches the speed of light
To a stationary observer, the mass of a particle travelling at relativistic velocity becomes heavier (dilated).
Mass is a measure of inertia
Inertia increases with velocity
The faster you go, the harder it is to accelerate
Mass-energy equivalence: If an object travels near speed c, doing work will not increase its speed, but its total mass → rest mass is a form of energy

Relativistic Momentum
Defined in such a way that the conservation of momentum will hold in all inertial frames
Relativistic momentum increases with velocity because mass increases with velocity
Relativistic momentum is measured using a body’s rest mass (m0) so the increase in momentum is only due to the increase in the body’s velocity.
Mass is dilated to conserve momentum for two observers in different FORs

Limiting Velocity
The limiting speed for any object with mass is the speed of light (c)
Space, gluons and photons don’t have mass → can travel at speed c or faster
The requirement for a particle to reach c is physically impossible and would break existing laws of physics

Mass-Energy Equivalence
Einstein also proposed that mass and energy are interchangeable
Mass can be converted into energy and energy can be converted into mass
Each quantity does not need to be conserved in its own form as they can inter-convert.
Doing work on an object will accelerate it and increase its energy
At low speeds, mass stays the same and speed increases → Increase energy
At high speeds, the speed stays the same and the relativistic mass increases → increase in energy
Conservation of mass and energy
Rest mass is a type of energy (stored energy), it can be transformed
Mass can be converted into other types of energy (rest mass decreases)
e.g. Moving an electron closer to the positive plate, some of its mass is converted into KE
Other types of energy can be converted into rest mass (rest mass increases)
e.g. using particle accelerators to collide particles into each other creates new particles with increased mass than both of the particles masses combined due to conversion if KE into mass
E=mc²

Mass-Energy Equivalence: Nuclear reactions in the Sun
Involve the rearrangement of protons and neutrons in the nucleus of atoms
Result in new nuclei being formed
Energy is absorbed if the proton and neutrons end up with more energy after the reaction
Energy is released of the protons and neutrons end up with less energy after the reaction
High temperatures are required
Nuclei need to get close to each other
Nuclei are positively charged
Temp provides energy (KE) to counteract the repulsive force between nuclei
Take place in the centre of stars (e.g. Sun)
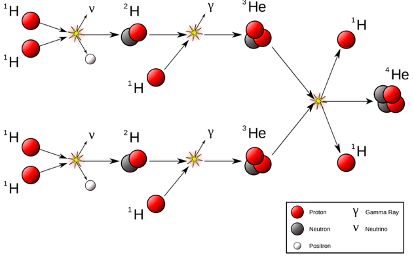
Hydrogen Fusion
4 Hydrogen → Helium + energy
4 protons → alpha particle (2 protons + 2 neutrons) + energy
Combine four protons (hydrogen nuclei) to make one alpha particle (helium nucleus)
This releases energy
The proton-proton chain is the main hydrogen fusion sequence that occurs in the Sun
Proton-proton chain
Two protons (2x 1H) collide to form deuterium (2H) and release a positron and a neutrino
Deuterium (2H) collides with a proton (H) to form Helium-3 (3H) and releases a gamma ray
Helium-3 then fuses with another helium-3 to form an alpha particle and releases two hydrogens
This alpha particle is a helium atom
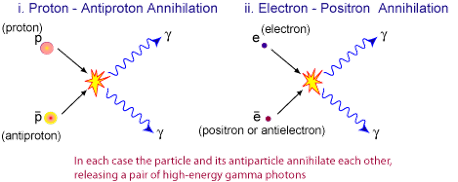
Mass-energy equivalence: particle–antiparticle interactions
Annihilation: Matter + Antimatter = energy
Two world consists of two groups of particles
Matter, consisting of:
Protons, neutrons, electrons make atoms
Unstable particles (e.g. muons, tau) that exist for short times
Antimatter
Every matter particle has a corresponding antimatter particle
Matter and antimatter particles have the same mass but opposite charge
When an annihilation reaction (pair annihilation) occurs:
All the masses of both particles convert into energy
Energy is released as two gamma rays (to conserve momentum)
Mass-energy equivalence: combustion of conventional fuel
Chemical reactions involve the rearrangement of electrons between different atoms
Result in the energy of electrons changing as new chemicals are formed
Energy can either be absorbed or released by chemical reactions depends on whether electrons finish with higher / lower energy
Depending on the precision of the measurements, we can see this change if measurements are imprecise, we will not see the mass change, since the energy released is so tiny
Combustion – chemical reactions where fuel is burnt (reacted with oxygen) to release energy
Fuel + oxygen → products + energy
e.g. Hydrogen + oxygen → water + energy
Conservation of energy requires energy on both sides of the equations to be the same
Since energy is released in the reaction, the mass of the products must be less than the combined mass of fuel and oxygen