AP Calculus AB Limits

How to interpret, lim x→c f(x) = L

“The limit as x approaches c of f(x) is L)

When does the limit not exist?

When the left limit doesn’t equal the right

What is a jump discontinuity and does it have a limit?

No it doesn’t have a limit

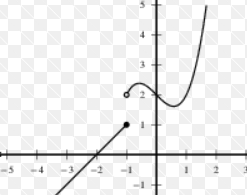
How do we interpret a graph that isn’t entirely continuous?

“yes it is continuous except at (blank)”

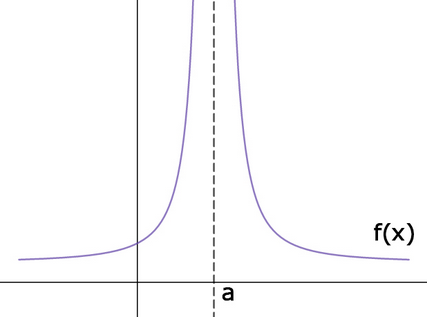
what is an infinite discontinuity and does it have a limit?

No it doesn’t have a limit

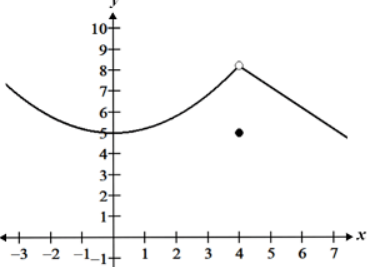
What is a removable discontinuity and does it have a limit

Yes it does have a limit

(blank) and (blank) are real numbers

• b

• c

lim x→c b = (blank)

b

“plug in” or limx x→c = (blank)

c

EX) lim x→0 x²/x = (blank)

lim x→0 x=0

EX) lim x→8 x²+x-72/x-8 = (blank)

(x-8)(x+9) / (x-8) = lim x→8 x+9

EX) lim x→c b * f(x) = (blank)

lim x→c f(x) = f(c)*b

Composition Function

lim x→c f(g(x)) = (lim x→c ^g(x))

Composition Function EXAMPLE) lim x→3 sin(x²+2) = (blank)

sin(lim x→3 ^x²+2) = sin(11)

lim x→c [f(x) +-/ g(x)] → (blank)

f(c) +-/ g(c)

if k is a positive constant then what does not exist?

• lim x→0⁺ k/x = ∞

• lim x→0^- k/x = -∞

• lim x→0 k/x

if k is a positive constant then what DOES exist?

• lim x→0⁺ k/x² = ∞

• lim x→0^- k/x² = ∞

• lim x→0 k/x² = ∞

what is the limit for lim x→∞ 1/x

0

if k and n are constants with n>0 then (blank)

lim x→∞ k/xⁿ = lim x→ -∞ k/xⁿ =0

The 3 requirements for Intermediate Value Theorum

1. F is continuous (limits exists everywhere) on the closed interval

2. [a,b], f(a) CANNOT equal f(b)

3. k is any number between f(a) and f(b)

EX) lim x→0 1/x², what is the limit?

∞

How to interpret Intermediate Value Theorem

since g(x) is continuous on the closed interval on [3,7] g(x) = a > b > c =g(y). Therefore by the intermediate value theorum there is such r that g(r) = #

1/0 = some #/ really small

∞

1/∞ = some #/huge number

0

∞/∞ =

anything

EX) lim x→∞ 3x²-6x+1/-2x²+8x+11

-3/2

When would you have a vertical asymptote?

lim x→80 f(x) = ∞

What variable does a horizontal asymptote use?

y

How to prove continuity

Since left + right hand limit are the same. Therefore f(x) is continuous at x = #

How to prove the limit exists at a number

since the right hand and left hand limit are the same. Therefore, final limit has to be true

EX) lim x→2 f(x) = 3

How to prove infinite discontinuity

Since both either the left hand, right hand or both equal infinity (+-). Therefore f(x) has an infinite discontinuity at #

How to prove jump discontinuity

since the left hand limit and the right limit are not equal. Therefore f(x) has a jump discontinuity at x = #

How to prove vertical asymptote

since the limit equals infinity. Therefore f(x) has a vertical asymptote at x = #

How to prove a removable discontinuity

EX) since lim x→2 f(x) = 4 and f(2) = 5. Therefore f(x) has a removable discontinuity at x = 2

How to prove horizontal asymptote

EX) since lim x→ ∞ f(x) = any #. Therefore f(x) has a horizontal asymptote at y = #

How to explain that I.V.T theorem does not apply

The intermediate value theorem dos not apply and I cannot prove it