Y10 Maths End of Year - things to remember

which way are brearings measured from

clockwise from the north

what does ‘bearing of b from a’ mean

start at a and go to b

how to set bearings out

using 3 digits e.g. 045 degrees

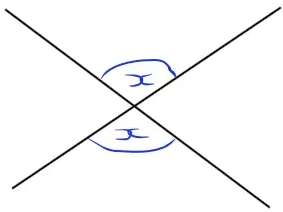
opposite angles are equal

x = x

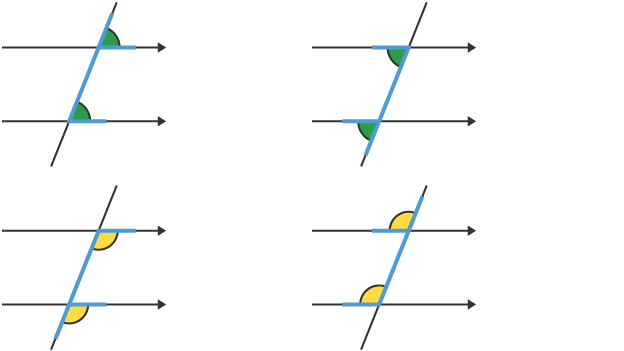
corresponding angles are equal

look for the f shape

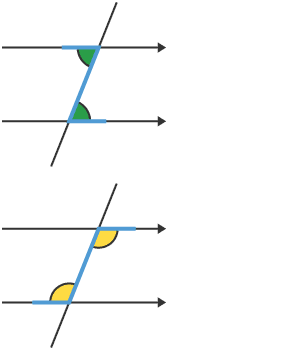
alternate angles are equal

look for the z shape

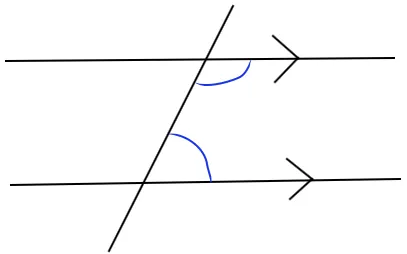
co-interior angles add to 180 degrees

the ambiguous case

If an angle is supposed to be obtuse but you’re getting an acute angle (or the other way round) subtract what you’re getting from 180 degrees

SOH CAH TOA

SOH: Sin = Opposite / Hypotenuse

CAH: Cos = Adjacent / Hypotenuse

TOA: Tan = Opposite / Adjacent

different sides for trigonometry (opposite, hypotenuse, adjacent)

Hypotenuse: always the longest (slanted) side

Opposite: always the side opposite the angle you’re trying to find

Adjacent: the side that is left over after the other two have been assigned, the one ‘next to’ the angle you’re trying to find out

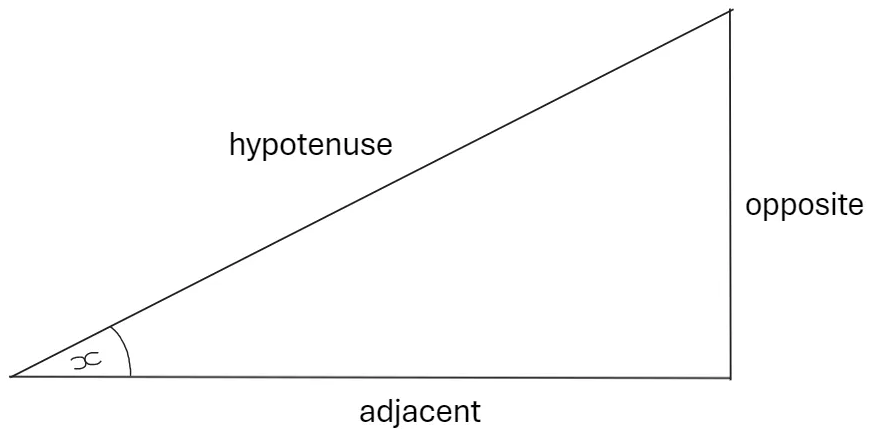
key fact about trig!

it only works with right-angled triangles

sine rule

sinA = sinB
a b

it also works flipped:

a = b
sinA sinB

a/b/c represent sides

A/B/C represent angles

the angle (capital letter) always goes with the sin, not the side

works with every triangle

always keep what you’re trying to find in the top (numerator) for easier rearranging

cosine rule

a² = b² + c² - 2bc cosA

Lower case letters = lengths, upper case letters = angles

a = the length you’re trying to find

A = the angle opposite the length you’re trying to find

b & c = the lengths on either side of A

Look for an two sides with an angle in between that you know

Don’t forget to square root a!

area of a non right angled triangle

½ a b sinC

You need two sides (a and b) and the angle between them (C)

acronyms for simultaneous equations

DSA: Different Signs Add

SSS: Same Signs Subtract

what does > mean

greater than

what does < mean

less than

what does ≥ mean

greater than or equal to

what does ≤ mean

less than or equal to

what type of bound does an empty circle show on a number line

number isn’t included: < or >

what type of bound does an shaded circle show on a number line

number is included: ≥ or ≤

what happens when you multiply/divide both sides of an inequality by a negative number?

you flip the inequality sign (< turns to > etc)

which type of line do you use for < or > when graphing inequalities

dashed/dotted line

which type of line do you use for ≥ or ≤ when graphing inequalities

solid line

what does a solid line mean when graphing inequalities

≥ or ≤

what does a dashed/dotted line mean when graphing inequalities

< or >

area of paralellogram

base x vertical height

area of rhombus

width x height (diagonals)
2

area of trapezium

½ (a+b) x h

formula for probability

number of ways the desirable event could happen / total number of possible outcomes

mutually exclusive events

events that can’t happen at the same time e.g. rolling a 3 and rolling a 6 on a dice

all probabilities of mutually exclusive events add to 1

independent events

events that have no effect on each other

to work out the probability you multiply them together:
P(A and B) = P(A) x P(B)

tree diagram rules

across the diagram = multiply

down the diagram = add

and / or

and = multiply

or = add

similar

same shape with same angles but a different size

congruent

same shape & same size but has been rotated/translated/mirrored etc

SAS

Side Angle Side - two sides and the angle between them

ASA

Angle Side Angle - two angles and the side between them

SSS

Side Side Side - all three sides

RHS

Right angle, Hypotenuse, Side

got it boss

got it 😘

ASF with VSF with LSF formulae

ASF = LSF²

VSF = LSF³

parts of a circle

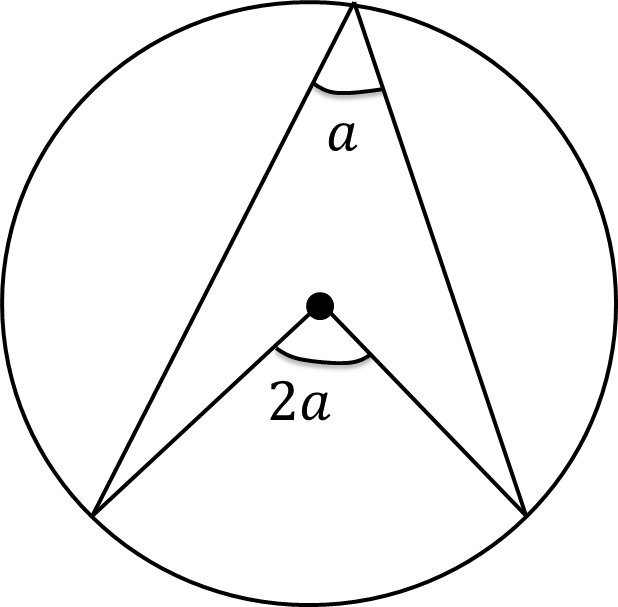
angle at the centre is 2x angle at the circumference - arrowhead

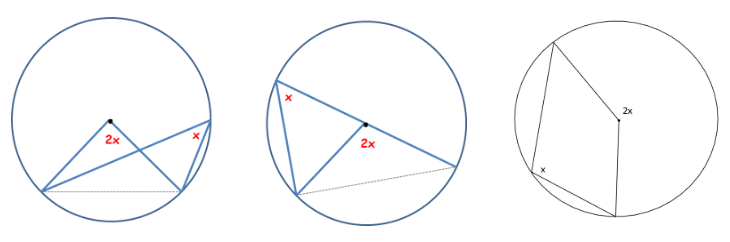
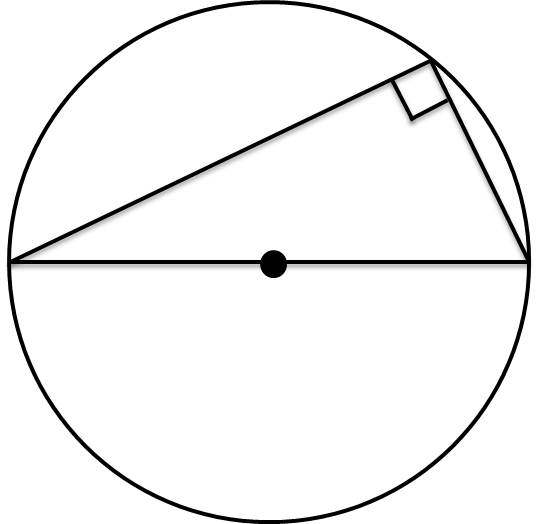
angle at the circumference in a triangle on the diameter is 90^o

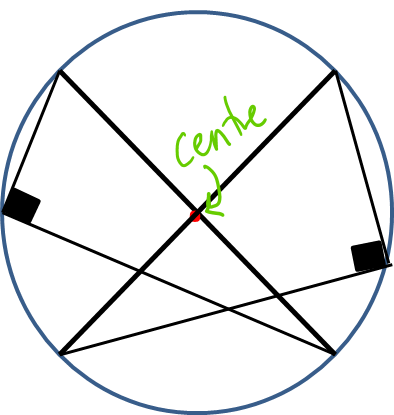
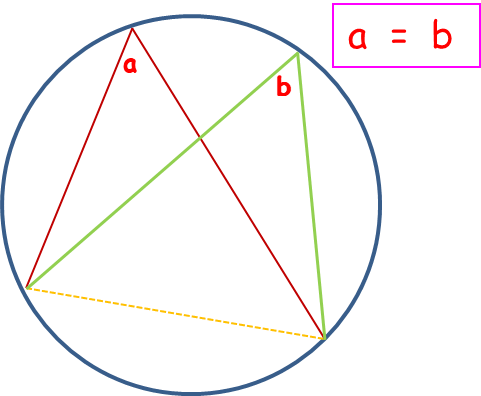
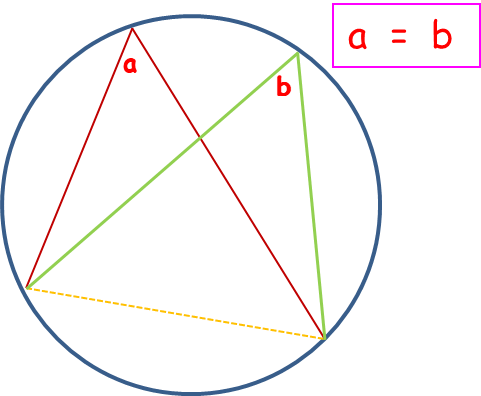
angles in the same segment are equal - butterfly

remember to stay in the same segment

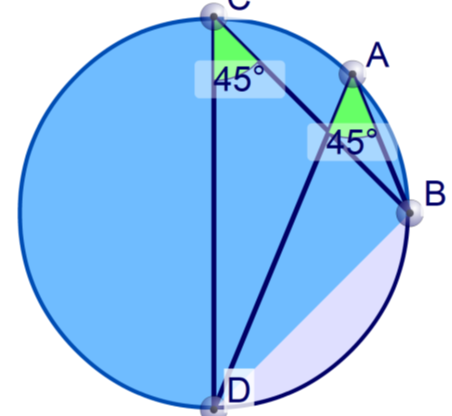
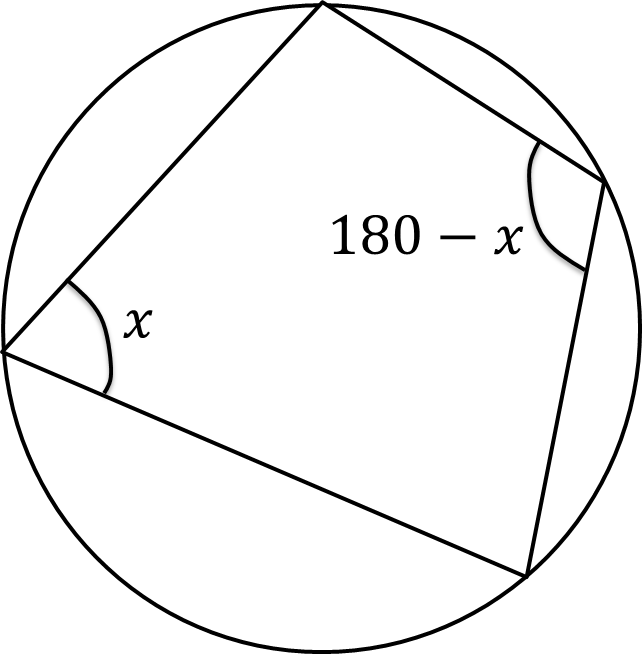
opposite angles in a cyclic quadrilateral add to 180^o

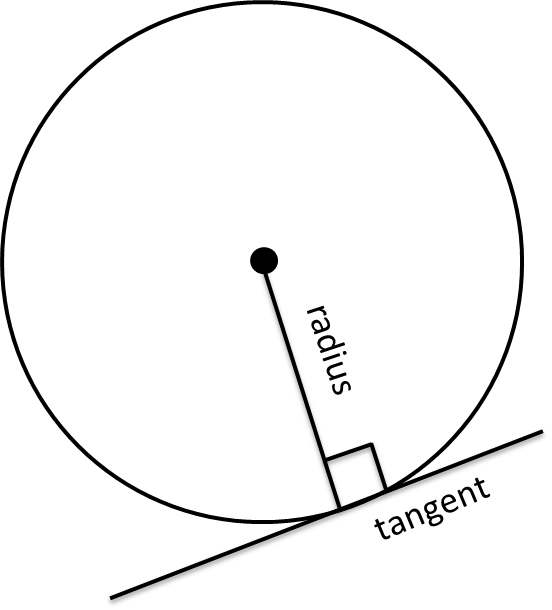
angle made by the tangent and radius is 90^o

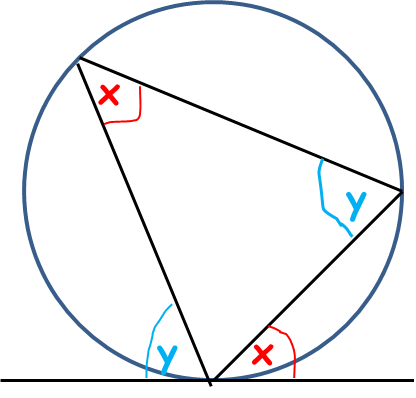
alternate segment theorem

look for a triangle (or just a chord) meeting a tangent

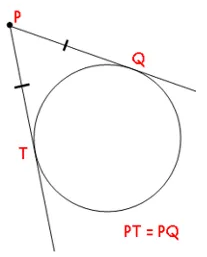
two tangents coming from the same point are the same length

often leads to an isosceles triangle

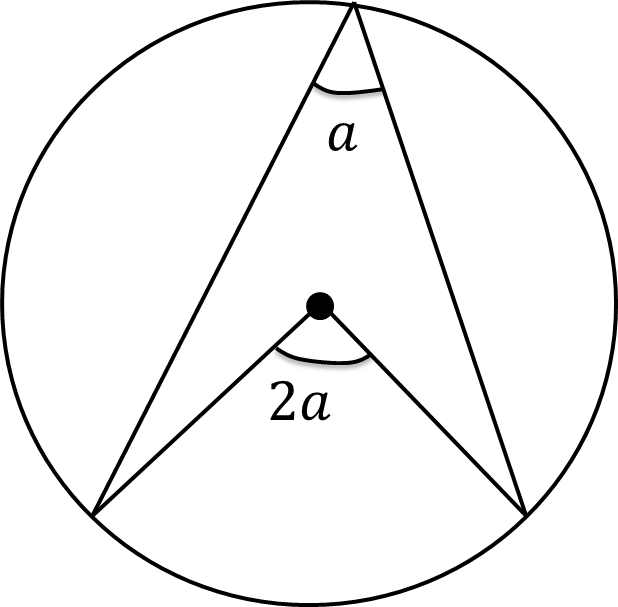
prove

1. Draw a line from O → B to split the arrowhead into two triangles

2. Triangles AOB and OBC are isosceles (shared side + bottom sides are both radiuses)

3. Therefore angles BAO and ABO are the same, and OBC and OCB are also the same (let them be x and y)

4. Angle AOB = 180° - x - x because angles in a triangle add to 180°, and angle BOC = 180° - y - y as well

5. Therefore angle AOC = 360 - (180-2x) - (180-2y)

6. You can expand this equation into 360 - 180 + 2x - 180 + 2y, then simplify it into 2x+2y as 360 - 180 - 180 = 0

7. Therefore angle AOC = 2x + 2y, or 2(x+y)

8. We also know that angle ABC is x+y

9. Therefore angle AOC is twice the size of ABC!

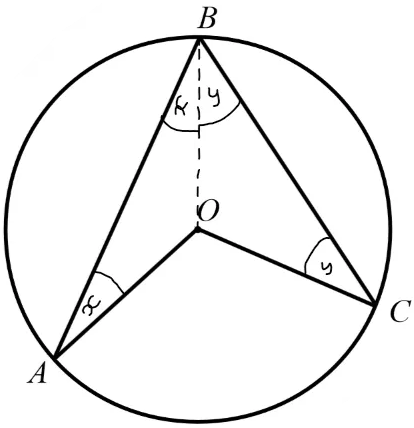
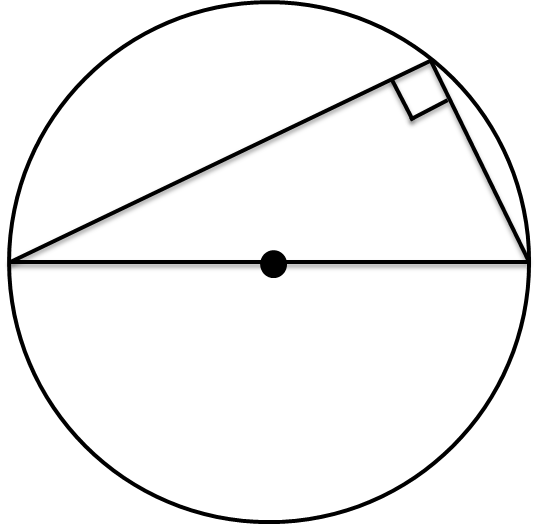
prove

1. Draw a line from O → B to split the triangle into two smaller ones

2. Triangles ABO and OBC are isosceles because AO, BO, and AC are all radiuses

3. So angles BAO and ABO are the same, and angles OBC and BCO are the same (let them be x and y)

4. Therefore the angles inside triangle ABC are x + x + y + y = 180°

5. Simplify this to 2x+2y = 180 and then 2(x+y) = 180 and then finally x+y = 90

6. So angle ABC is 90°

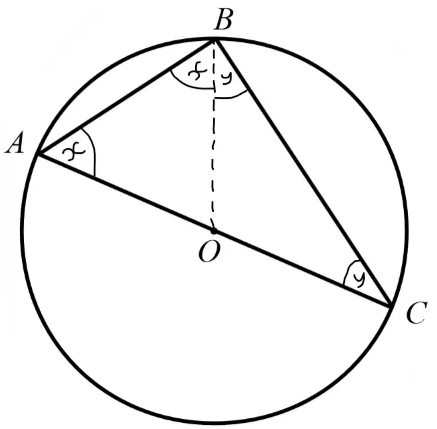
prove

1. Let angles ABD and ACD be x and y

2. Draw a line from A→O→D to create an arrowhead

3. Using the arrowhead theorem, angle AOD is 2x and also 2y

4. Therefore we can say that 2x = 2y, and then that x=y

5. Therefore angles ABD and ACD are the same!

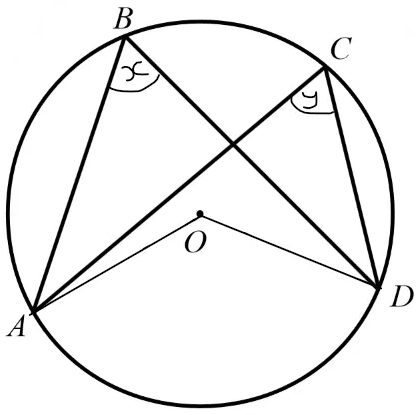
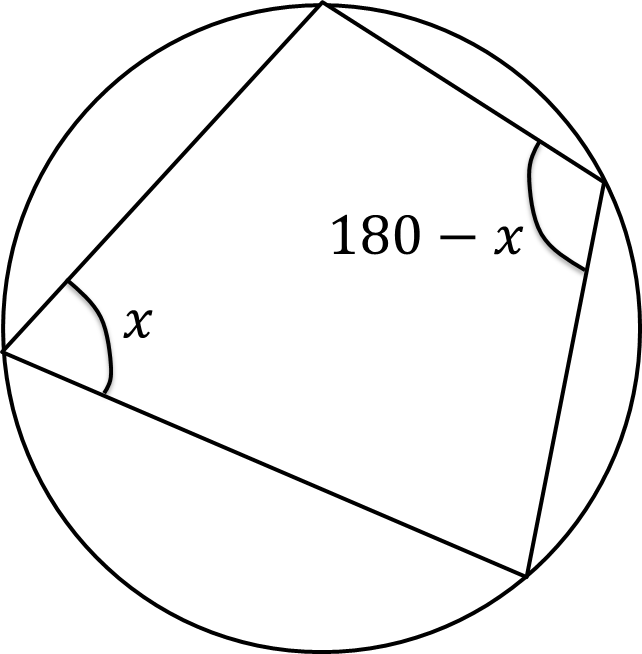
prove

1. Draw a line from A→O→C to split the quadrilateral into two smaller quadrilaterals

2. Call angle ABC x and angle ADC y

3. Using the arrowhead theorem, the two angles at AOC would be 2x and 2y

4. You know that these two angles added together made 360° (2x+2y=360°) because of angles around a point

5. You can simplify this equation to x+y=180°, proving this theorem

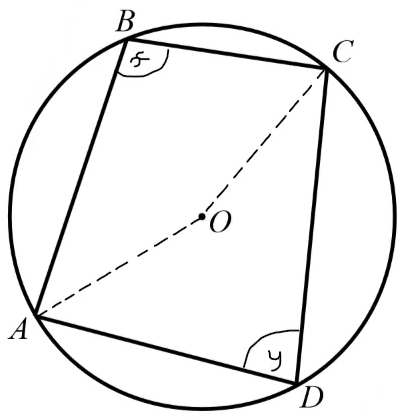
prove

1. Draw a line from C→O→B to create a smaller triangle

2. This triangle (OBC) is isosceles as OC and OB are both radiuses

3. Therefore you can label OCB and OBC as both x

4. Angle OCE is 90° using the tangent and radius theorem, so if angle OCB is x, angle BCE is 90-x

5. Using the arrowhead theorem, you can label angle CAB as y and COB as 2y

6. Using everything we’ve labelled so far, we can use angle facts in triangle OCB and say that 2x + 2y = 180°

7. You can simplify this to x+y=90°, and then rearrange to say that y = 90-x

8. As angle BCE is 90-x, and CAB is y, they are the same

arithmetic sequence

terms increase/decrease by the same amount each time

e.g. 1, 2, 3, 4, 5 or 3, 5, 7, 9, 11

geometric sequence

consecutive terms are found by multiplying/dividing by the same value (the common ratio)

e.g. 2, 4, 8, 16

quadratic sequence

where the nth term is a quadratic (form of an²+bn+c)

finding the nth term of arithmetic sequence

bn + a

where b = the difference between the terms
and a = the term before the first term (n=0)

finding the nth term of geometric sequences

use the common ratio - number you multiply each term by to get to the next. you find it by dividing one term by the one before it

a x r^n-1

where a = the first term of the sequence

and r = the common ratio

finding the nth term of quadratic sequences

1. Work out the difference between each pair of terms

2. Work out the second difference - the difference between the differences.

3. Divide the second difference by 2 to get the coefficient of the n² term. Write this down.

4. For each term in the sequence, work out the coefficient of the n² term you just worked out, subbing 1, 2, 3 etc into n for each term.

5. Now subtract those numbers you just worked out from each term in the original sequence (term - coefficient) to give a new sequence

6. Work out the nth term of this new sequence, and simply add it onto the end of the coefficient you worked out in step 3.

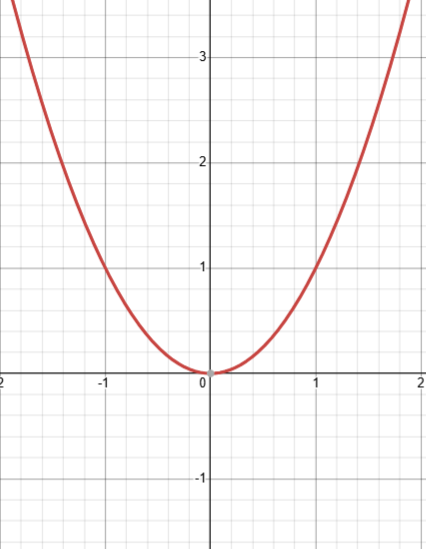
quadratic graphs

equation in the form ax² + bx + c

graphs are symmetric with one turning point. the u-shaped part is called a parabola.

if the coefficient of x² is positive then the graph looks like a regular U-shape. if the coefficient of x² is negative then the graph looks like an upside-down U-shape

the ‘c’ part (the last number on its own) is the y-intercept.

the roots (solutions) of the equation are where the curve crosses the x-axis

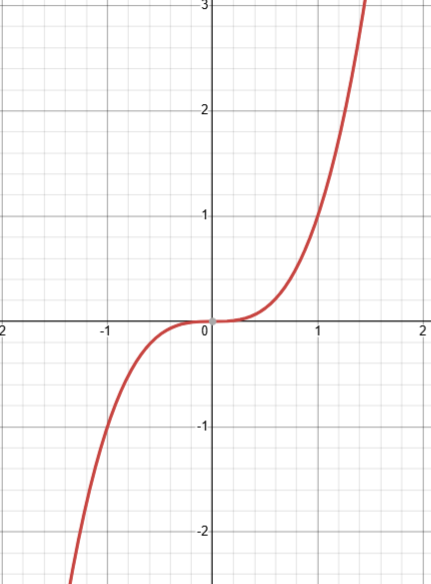
cubic graphs

of the from ax³ + bx² +cx + d. graphs have the shape of a curve with a wiggle in the middle.

if the coefficient of x³ is positive, the wiggle goes from down to up (looking left → right). if the coefficient of x³ is negative, the wiggle goes from up to down (looking left → right)

graphs have two turning points.

‘d’ part (the last number on its own) tells you the height - how shifted up/down the graph is

roots (solutions) are where the curve crosses the x-axis

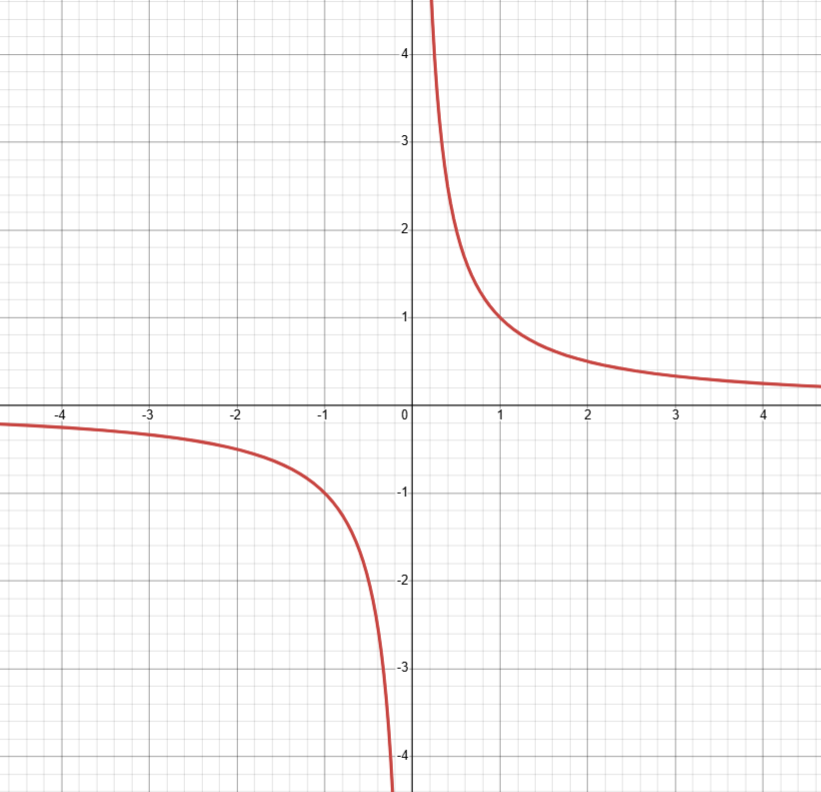
reciprocal graphs

in the form a
f(x)

where f(x) means a function of x e.g. x+1

you can recognise them by them having a fraction in them

reciprocals don’t have values for every value of x - since we can’t divide by 0, the denominator can’t every be 0, so when the denominator is zero the function is undefined. this makes reciprocal graphs have asymptotes - lines that the graph gets very close to but never touch. they’re represented as dotted lines

to plot reciprocals, think about the asymptotes and draw them in first

if the denominator is squared, the reciprocal will have only positive values, so the two lines will be in the top two quarters of the graph (instead of in opposite quarters). the opposite applies if x is negative and squared

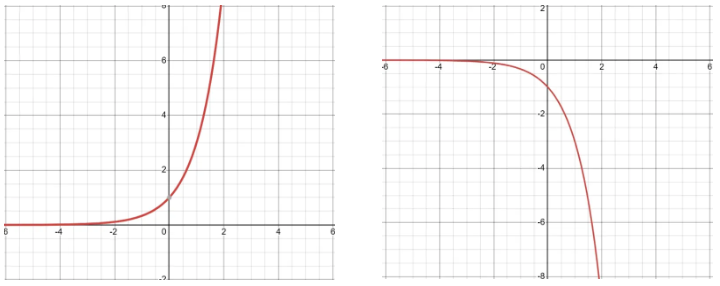
exponential graphs

form y = a^x

when a is bigger than 1, a^x gets very high very quickly, and as it decreases a^x gets smaler but never touches 0 - the x-axis is an asymptote. the opposite is true if a is smaller than 1

all exponential graphs go through the coordinate (0,1)

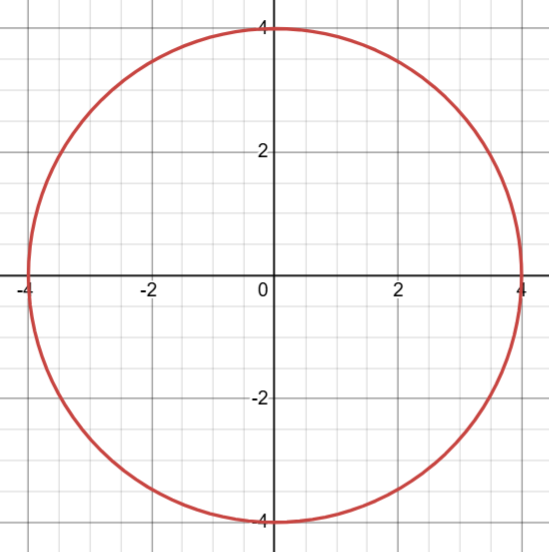
circle graphs

in the form (x - a)² + (y - b)² = r² where r is the radius, and the circle’s centre is at (a, b) remember with the opposite signs as in the equation

if there are no numbers attached to the x or y like x² + y² = 16 then the centre is at (0,0)

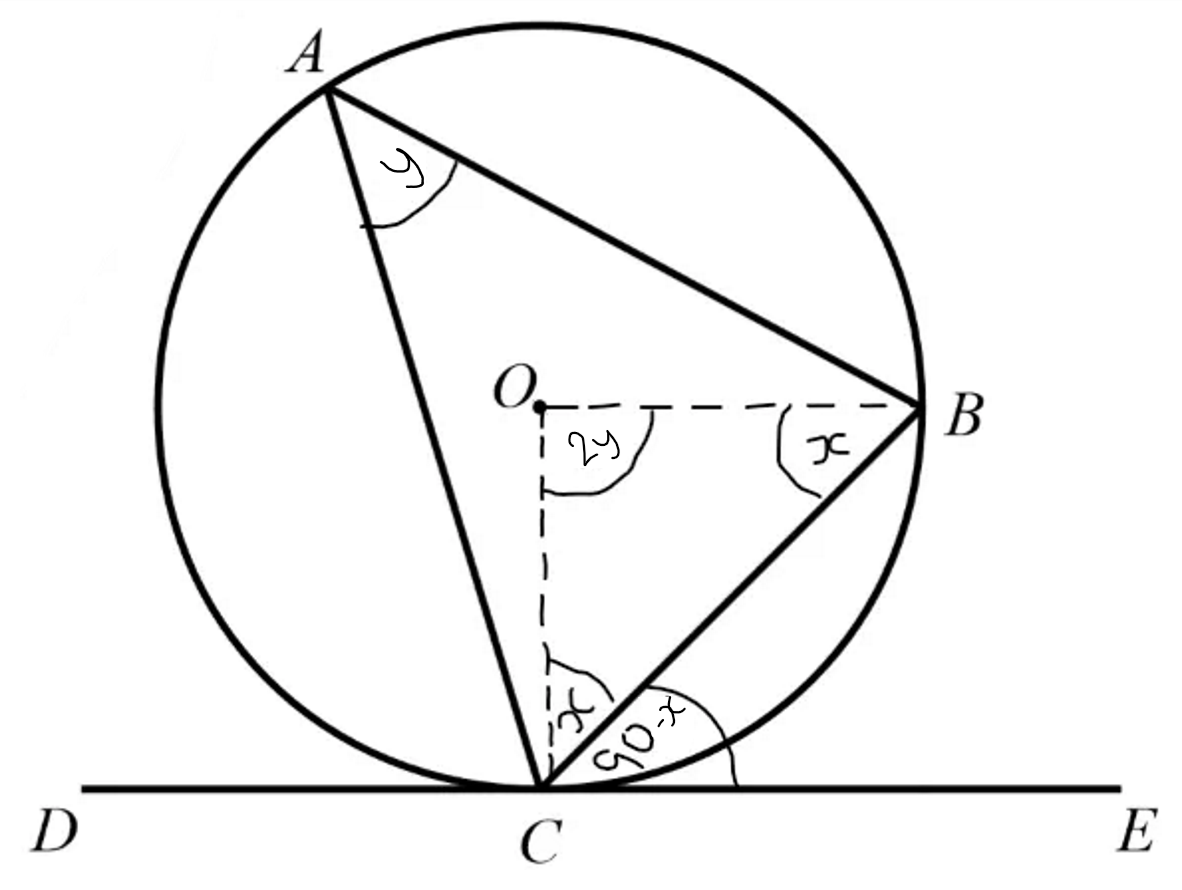
finding the equation of a tangent

1. find the gradient of the radius (rise/run)

2. find the gradient of the tangent (negative reciprocal of radius gradient)

3. find the c part of the equation (sub the coordinates you know into the equation)

4. put it all together into y = mx + c

how many mg in a g

1000mg

how many kg in a tonne

1000kg

how many ml in 1cm³

1ml

circumference of a circle

2πr

area of a circle

πr²

arc length of sector

angle x 2πr
360

area of sector

angle x πr²
360