STATS FINAL: Chi-Square Tests

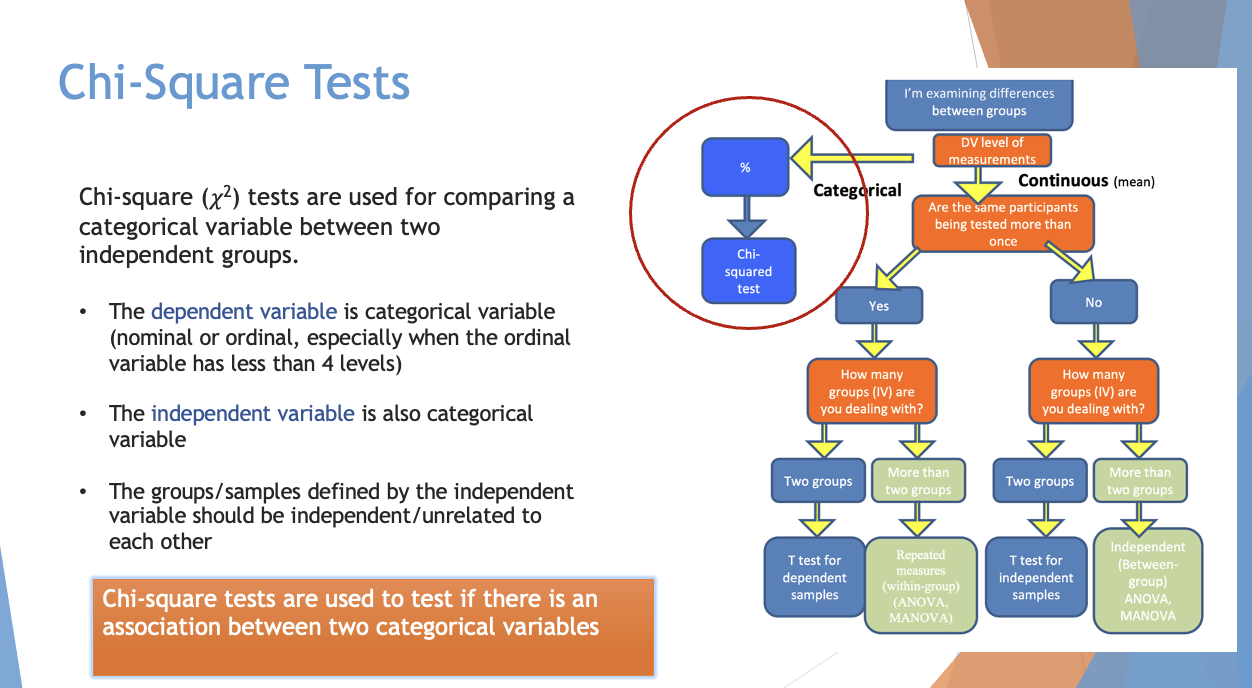
What are chi-square tests?

they’re used for comparing a categorical variable between two independent groups

• the responding variable is categorical (nominal or ordinal)

• Independant variable is also categorical

**•The groups/samples defined by the manipulated variable should be independent/unrelated to each other

What are the key characteristics of a chi-square test?

• a non-parametric test ==> doesn’t rely on underlying assumptions like normality because it’s specifically designed for categorical data

  •  where the data information contain counts or frequencies

• Focused on frequency distributions: uThe chi-square test examines the distribution of observed frequencies in comparison to expected frequencies under a specific hypothesis.

What are the assumptions for a chi-square test:

• independence of observations ==> a must

• Mutually Exclusive Categories ===>Each observation belongs to only one category per variable.

• categorical data for both manipulated and responding variable

• Sufficiently Large Expected Frequencies

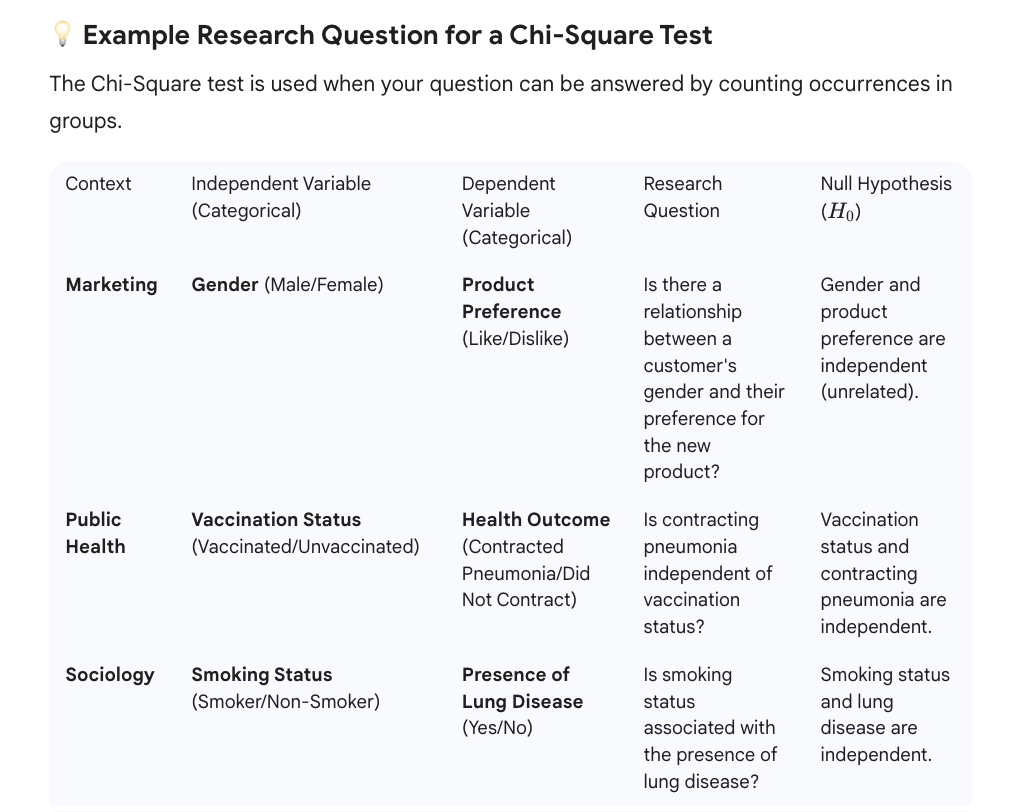
Chi-Square test is used when you have two or more categorical variables and you want to see if they are related (dependent) or independent (unrelated).

So the “experiment” revolves around things like:

In short, the Chi-Square test determines if the proportions of one category (e.g., the proportion of "Likes") are the same across the groups of the other category (e.g., Male vs. Female).

What is a contingency table:

A Contingency Table (also called a cross-tabulation or cross-tab) is a table that displays the frequencies (counts) of observations for every combination of your two categorical variables.

Observed vs. Expected frequencies:

observed ==> what we actually count

expected ==> what the count should be if the null hypothesis were true

• Observed Frequencies ($O$): These are the actual counts you recorded in your study, representing the real-world data collected for each combination of categories (the numbers inside the contingency table cells).

• Expected Frequencies ($E$): These are the counts you would theoretically expect to find in each cell if there were absolutely no relationship between the two variables (if the null hypothesis were true).

The Chi-Square test then compares $O$ and $E$;

• the bigger the difference between what you observed and what you expected, the stronger the evidence that the two categorical variables are actually related.

What is the null hypothesis for a chi-square test?

Null (H₀​): There is no association between the two categorical variables (they are independent).

** SO WE ASSUME INDEPENDENCE BECAUSE WE’RE TRYING TO TEST IF THERE IS AN ASSOCIATION

for us to use a chi-square test, the expected frequency has to be:

greater or = 5, if it’s less we use fisher’s test

What is the statistic we calculate for chi-square test?

•𝜒²-statistic

How do we calculate expected frequency for per cell?

	Respiratory Disease (Yes)	Respiratory Disease (No)	Total
Smoke	50 (A)	30 (B)	80 (A+B)
Non-smoker	20 (C)	100 (D)	120 (C+D)
Total	70 (A+C)	130 (B+D)	200 (A+B+C+D)

row x colum/total

How do we calculate 𝜒²-statistic?

Each cell has an expected frequency of at least 5. We can use a standard chi-square test.

Degrees of freedom for a chi-square test is:

Df = (r−1) * (c−1)

where r is the number of rows and c is the number of columns.

Rows are horizontal: ROW HO

columns are vertical

The calculated 𝜒²-statistic has to be > than the critical value (find via. a and df), we reject null

Then there is an association

What are the limitations of chi-square tests?

uHighly sensitive to sample size

uSensitive to small frequencies (<5)

uIt does not provide information about the strength and direction of the relationship.

The Chi-Square test determines if a statistical relationship exists between two categorical variables by comparing the counts you observed to what you expected under the assumption of no link.

However, its limitation is that a significant result only confirms the association and does not tell you the strength, direction, or where exactly the differences lie within the categories. ==> like if smoking cause pneumonia.

What is the fisher’s exact test?

• used when any expected frequencies are less than 5