Unit 4: Probability, Random Variables, and Probability Distributions
1/106
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
107 Terms
What is the nature of chance behavior?
it is unpredictable in the short run, but has a regular and predictable pattern in the long run
What does a random process do?
generate outcomes that are determined purely by chance
What is a trial?
one repetition of a random process
True or false: The probability of any outcome of a chance process is always a number between 0 and 1
true
What does probability describe?
the proportion of times the outcome would occur in a very long series of repetitions
What does the law of large numbers state?
that if we observe more and more repetitions of any chance process, the proportion of times that a specific outcome occurs approaches its probability
True or false: Probability allows us to make short-run predictions
false
What does the law of averages assume?
that the results of a chance process have to even out in the short run
Why is the law of averages a misguided belief?
future outcomes are not affected by past behavior; past outcomes do not influence the likelihood of individual outcomes occurring in the future
Ex / According to the Bood of Odds website, the probability that a randomly selected U.S. adult usually eats breakfast is 0.61. Explain what probability 0.61 means in this setting
If you take a very large random sample of U.S. adults, about 61% of them will say they eat breakfast
What does the sum of probabilities in a probability model always equal?
1
What is the probability when an outcome is impossible and can never occur?
0
What is the probability when an outcome is certain and will occur on every trial?
1
What is the probability when an outcome is very unlikely but will occur once in a while in a long sequence of trials?
0.001
What is simulation?
the imitation of chance behavior, based on a model that accurately reflects the situation
What is the simulation process?
ask a question about the chance process
describe how to use a chance device to imitate one trial (repetition) and tell what you will record at the end of each trial
perform many trials of the simulation
use the results of your simulation to answer the question of interest
What is the purpose of simulation?
to estimate probabilities that are difficult to calculate theoretically; to represent experimental probabilities
What is a probability model?
a description of some chance process that consists of two parts:
a list of all possible outcomes
a probability for each outcome
What is the sample space ‘S’ of a chance process?
the list of all possible outcomes
What do probability models allow us to find?
the probability of any collection of outcomes
What is an event?
any collection of outcomes from some chance process
What events usually designated by?
capital letters
ex / probability of rain → P(R)
What is the probability that event A occurs if all outcomes in S are equally likely?
(number of outcomes in event A) / (total number of outcomes in sample space)
What is the probability that an event does NOT occur?
one minus the probability that the event does occur
P(AC) = 1 – P(A), AC is the complement of event A
What is the probability of two events that have no outcomes in common?
the sum of their individual probabilities
P(A or B) = P(A) + P(B)
What does P(A ∩ B) mean?
P(A and B)
What does P(A ∪ B) mean?
P(A or B)
When are two events mutually exclusive (disjointed)?
if they have no outcomes in common and therefore can never occur together
What is the addition rule for mutually exclusive events?
P(A or B) = P(A) + P(B)
How do you show that a probability model is legitimate?
by stating that the probabilities add up to 1 and all the probabilities are between 0 and 1
What is a Venn diagram?
one or more circles surrounded by a rectangle
What does each circle in a Venn diagram represent?
an event
What does the region inside the rectangle of a Venn diagram represent?
the sample space of the chance process
When is an observed result of a simulation statistically significant?
when the probability of getting that result is less than 5%
What is conditional probability?
the probability that one event happens given that another event is already known to have happened
What does P(A|B) mean?
the probability that event A happens given that event B has happened
What does P(B|A) mean?
the probability that event B happens given that event A has happened
What is the formula for the conditional probability P(A|B)?
P(A and B)
−−−−−−−−−−
P(B)
When are two events independent?
if knowing whether or not one event has occurred does not change the probability that the other event will happen
When are events A and B independent?
P(A|B) = P(A|Bc) = P(A)
When are events B and A independent?
P(B|A) = P(B|Ac) = P(A)
What is the multiplication rule for independent events?
If A and B are independent events, then the probability that A and B both occur is:
P(A and B) = P(A ∩ B) = P(A) × P(B|A)
What is the difference between “mutually exclusive” and “independent”?
mutually exclusive events are completely separate and cannot occur at the same time, while independent events can happen together without influencing each other
What does a tree diagram show?
the sample space of a chance process involving multiple stages, where the probability of each outcome is shown on the corresponding branch of the tree
Which probabilities on a tree diagram are conditional?
all probabilities after the first stage are conditional
What is a very common way to lose credit on probability questions?
not showing work
When is it better to use a tree diagram than a two-way table?
when you have multiple stages to be tested
What is a random variable?
a variable that takes numerical values that describe the outcomes of a random process
What does a probability distribution of a random variable give?
the random variable’s possible values and their probabilities
What does a probability model describe?
the possible outcomes of a chance process and the likelihood that those outcomes will occur
What is a discrete random variable?
a random variable that takes a fixed set of possible values with gaps between them
What is the mean (expected value) of a discrete random variable?
the average value of the discrete random variable over many, many repetitions of the same chance process
How do you calculate the mean (expected value) of a discrete random variable?
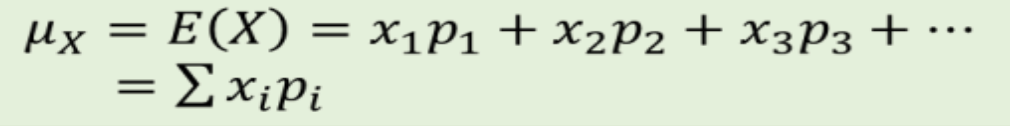
Does the expected value of a random variable have to equal one of the possible vales of the random variable?
no
What is the formula for the variance of a discrete random variable, X?
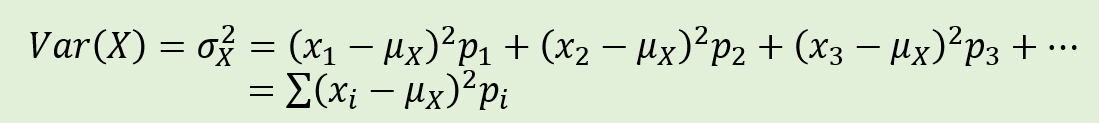
What is the formula for the standard deviation of a discrete random variable, X?
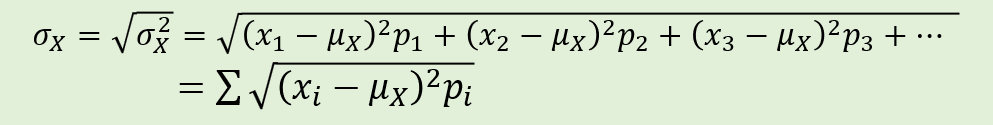
What is the interpretation for the mean of a discrete random variable?
The mean of [x] of many, many randomly selected [individuals] is [mean]
ex: The mean tuition spent by many, many randomly selected students from both the main campus and the downtown campus of El Dorado Community College is $1557.50
What is the interpretation for the standard deviation of a discrete random variable?
The [x] of many, many randomly selected [individuals] typically varies by about [standard deviation in units] from the mean of [mean in units]
ex: The number of languages spoken by many, many randomly selected U.S. high school students typically varies by about 0.671 languages from the mean of 1.457 languages spoken
What is a continuous random variable?
a random variable that can take any value in an interval on the number line
What is the probability distribution of a continuous random variable described by?
a density curve
What is the probability of any event involving a continuous random variable?
the area under the density curve and directly above the values of the horizontal axis that make up the event
What does the area under a density curve always equal?
1
What is the probability of an exact value for a continuous random variable?
always 0
What are measures of center?
mean, median, quartiles, maximum, minimum, and percentiles
How does multiplying or dividing a random variable by a constant affect measures of center?
measures of center are multiplied/divided by the constant
What are measures of variability?
standard deviation, IQR and range
How does multiplying or dividing a random variable by a constant affect measures of variability?
measures of variability are multiplied/divided by the absolute value of the constant
How multiplying or dividing a random variable by a constant affect shape?
shape doesn’t change
How does adding or subtracting a constant to/from a random variable affect measures of center?
the constant is added or subtracted to/from measures of center
How does adding or subtracting a constant to/from a random variable affect measures of variability?
measures of variability don’t change
How adding or subtracting a constant to/from a random variable affect shape?
shape doesn’t change
In general, if X is a random variable, then
µa+bX =
a + b(µx)
In general, if X is a random variable, then
σ2x =
b2(σ2x)
In general, if X and Y are independent random variables, then
µx+y =
µx + µy
In general, if X and Y are independent random variables, then
σ2x+y =
σ2x + σ2y
In general,
µnX =
n(µx)
In general,
σnX =
|n|σx
In general,
σ2nX =
n2(σ2X)
In general,
µx1+x2+….xn =
n(µx)
In general,
σx1+x2+…xn =
√n (σx)
In general,
σ2×1+x2+…xn =
n(σ2x)
What is a linear transformation?
random variable X → y = ax + b
µy = a(µx) + b
σy = a(σx)
What is a binomial setting?
when we perform n independent trials of the same chance process and count the number of times a “success” occurs
What are the conditions for a binomial setting?
BINS – binary, independent, number, same probability
What is the binary condition for a binomial setting?
the possible outcomes of each trial can be classified as “success” or “failure”
What is the independent condition for a binomial setting?
trials must be independent
What is the number condition for a binomial setting?
fixed number of trials
What is the same probability condition for a binomial setting?
same probability of success on each trial
What is a binomial random variable?
the count of success x in a binomial setting
What are the parameters of a binomial distribution?
x ~ BIN (n, p, k), where n = number of fixed trials, p = probability of success, and k = number of success desired
What is the most common mistake students make on binomial distribution questions?
failing to identify that it is a binomial distribution
When is binompdf used?
when you are trying to find the probability of an exact number of successes
When is binomcdf used?
when you are trying to calculate the sum of probabilities up to k
What is the binomial coefficient?
the number of ways to arrange k successes among n trials
What is the formula for binomial coefficient?
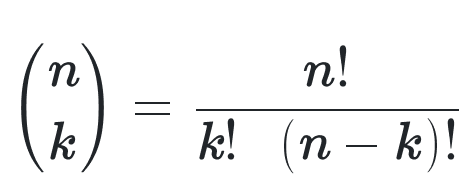
What is binomial probability?
the probability of getting exactly k success in n trials
What is the formula for binomial probability?
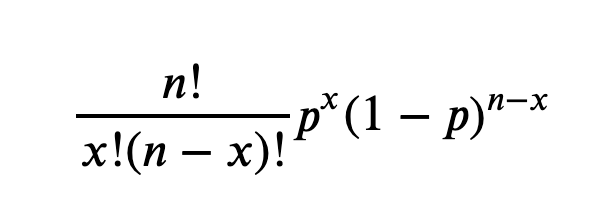
What is the mean of x in a binomial distribution?
µx = np
What is the standard deviation of x in a binomial distribution?
σx = √np(1-p)
How can an SRS be considered virtually independent and thus binomial if sampling is done without replacement?
if it satisfies the 10% condition, in which
n ≤ 1/10N or 10n ≤ N