Relational Data Structures - Week 4

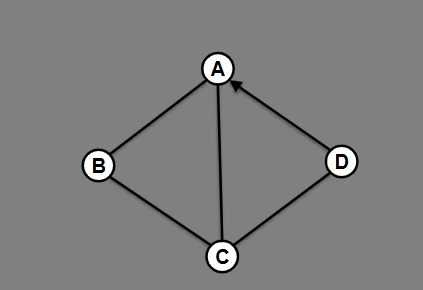
For this graph, show the adjacency matrix. And how would this be different if it was weighted?

If weighted, the 1s would be changed to the weight.

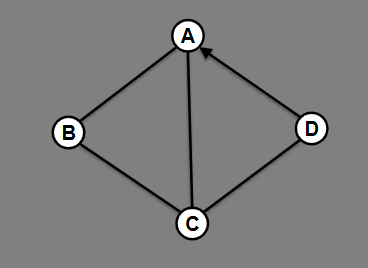
For this graph, give the adjacency list and edge list.

If a graph is undirected, how does this alter the edge list?

Only list the pairs once.

What is a tree?

A graph with no loops. It has vertices and edges.

What is the weight of the graph?

The length of the path back to the root.

What is a subtree?

Any collection of vertices and
edges from the tree which remains a tree.

Parial orders and total orders in trees. How are they defined?

Vertex orders are defined using the height.

A =< B because height(A) =< height(B).

This is only a partial order; doesn’t allow comparisons at the same level.

To get a total order, we must arbitrarily define the order of the children of a vertex.

What does a partial order mean about a tree and what does a total order allow?

Partial order means it is not linear.

Total order allows to sort the vertices of a tree.

How many edges does a tree have?

A tree with n vertices has n-1 edges.

Prove a tree with n vertices has n-1 edges.

→ Every edge joins a parent to 1 child. Take the edge joining parent to child and associate with the child.

→ Each vertex, except the root, has exactly one edge associated, hence n-1 edges.

What is the size of data for a tree?

O(1)

Why is an adjacency matrix not used for trees?

Highly redundant, has size O(n²)

What is a binary tree?

A tree where each vertex has at most 2 children.

What representation is used in binary trees?

Array.
At each level k, at most 2^k vertices. Requires array size: 2^h+1-1

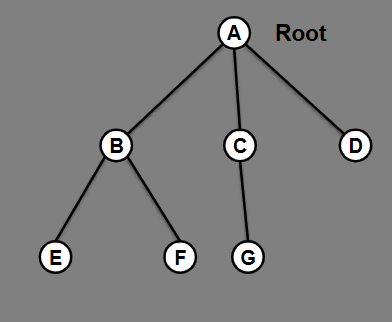
What is the adjacency list for this tree?

A(B,C,D)
B(E,F)
C(G)
D()
E()
F()
G()

What is the purpose of a heap?

In some problems, we have data where the ordering ‘=<' represents a priority. The highest priority item is the minimum in regards to (w.r.t) =<.

We would like to represent this data in an efficient data structure that allows us to recover the minimum item and insert new data.

This is the purpose of a heap.

How can heaps be defined as binary trees?

→ It is complete - every level is full, except for (possibly) the last one. Items on the last row are left justified.

→ Each vertex represents 1 item of data.

→ The value on a vertex is no more than that of any of its descendants.

→ Therefore, any subtree is also a heap.

Properties of binary heaps

Since the tree is binary and complete, we represent it efficiently with an array with 2^h+1-1, with h = O(log2n) number of items.

The root is the smallest element and can be found in O(1) time.

A new item is inserted in the next position in the final row, done in O(1) time.

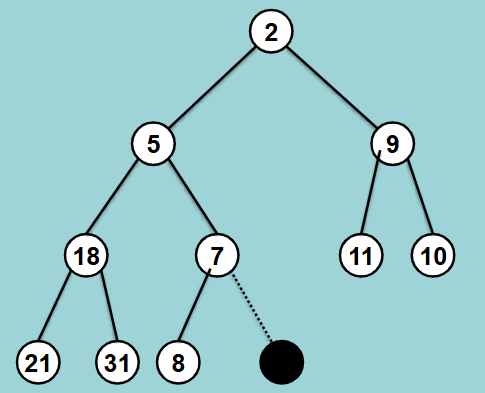
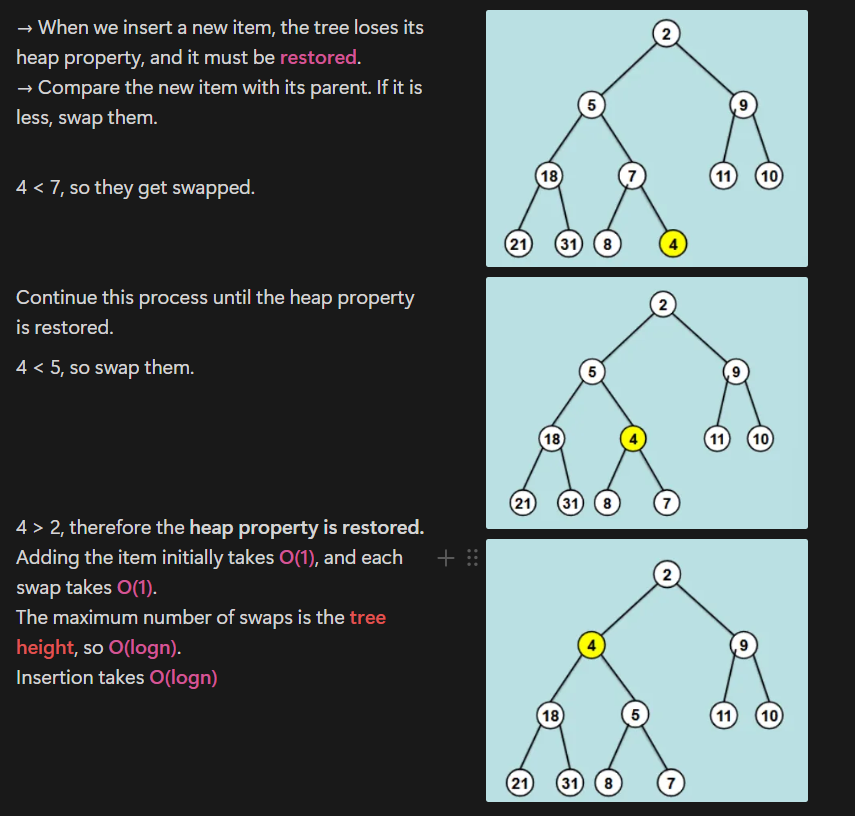
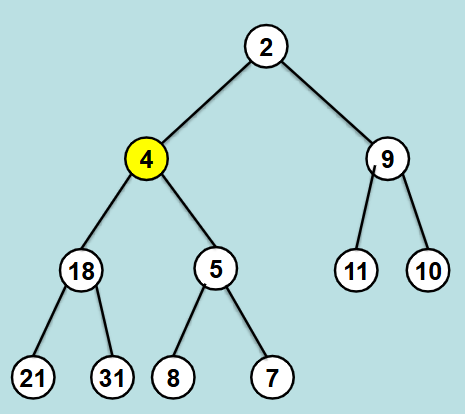
Show the steps to insert the number ‘4’ into a tree with a binary heap property.

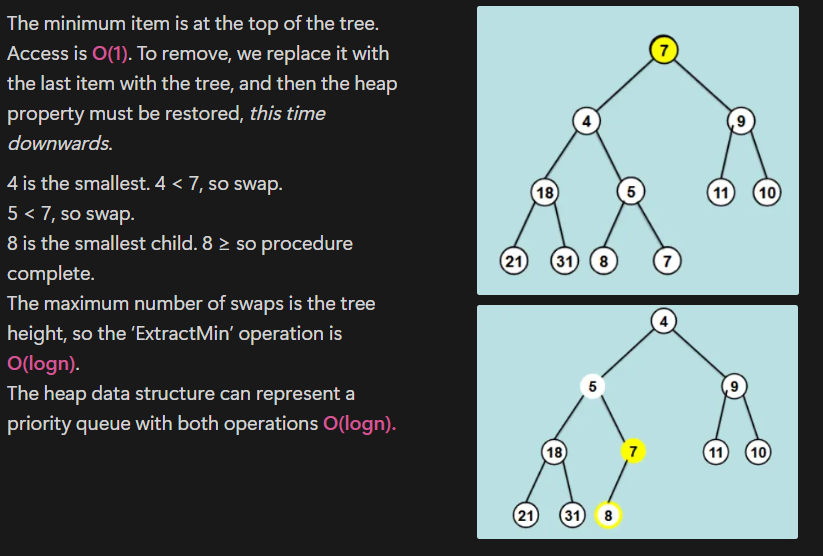
Show the steps to extract the minimum vertex in this binary tree with a heap function.

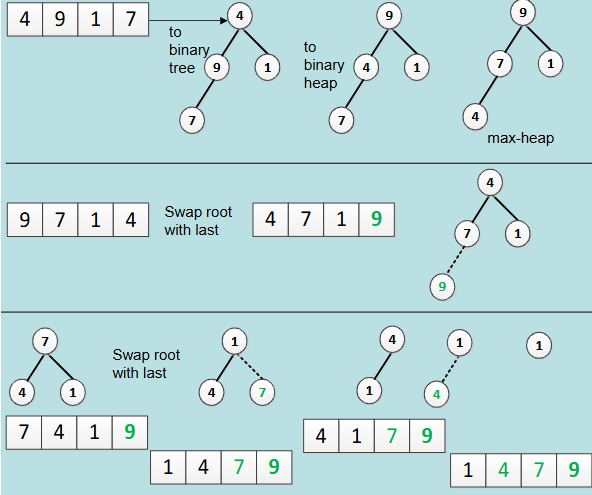
What are the steps to perform a heap sort on an unsorted array O(n)

1. Build a heap from unsorted array O(n)
   → Convert unsorted array into a binary tree.
   → Convert tree to binary (max) heap.

2. Sorting:
   → Swap root elements with last element. It will be ordered and not considered further.
   → Rebuild heap for remaining.
   → Repeat a and b until the heap is of size 1.
   → Array is sorted.

Show the performing of a heap sort on this unsorted array: