AP Statistics Chapter 3

For what type of variables should we use a scatterplot?

What should we include when creating a scatterplot?

2 quantitative variables

Explanatory = x-axis

Response = y - axis

key points to cover when describing a scatterplot

FoCUSeD

Form: _________

Context: ______

Unusual: points that deviate from the pattern

Strength: ________

Direction: _______

linear, curved, scattered

explanatory + response variables

strong, moderate, weak

positive or negative

What is a succinct way of describing scatterplots?

There is a strength, direction, form relationship between explanatory and response, with unusual points.

Correlation measures the ___ and ___ of the ____ relationship btwn 2 quantitative variables

r is _____ if x and y are interchanged.

r is _____ if x and/or y are rescaled.

r units:

strength, direction, linear

umchanged

unchanged

none

What is that range of correlation, what values translate to a strong or weak correlation?

-1 to 1, |coefficient| —> .9 to 1 = A, .8-.9 = B, etc. (weaker as u get closer to 0)

How to calculate correlation coefficient (r) when given data points?

1. make table with __,__ ,__ ,__ , __ for each value

2. find mean and standard deviations of x values and y values

3. find _____ of each x and y value based on that, then the product

4. ___ the products, divide by ____

x, y, zx, zy, product of zx * zy

z scores, product

add, n-1

Residuals: The error (vertical distance) between a linear model’s prediction and the observed data point.

Residual = ______

actual value - predicted value

y-ŷ

least squares regression line form

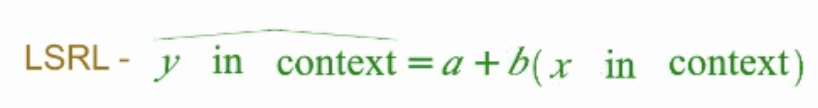
Interpret the slope in context.

As x increases by 1 unit, y is predicted to increase by b units

x and y shud be in context

Interpret the y-intercept in context. Use this sentence stem:

When x is zero units, y is predicted to be a units.

x and y shud be in context

the unique line that minimizes the sum of the squares of the vertical distances (residuals) between each data point and the line itself, predicts a value of y for a given value of x

least-squares regression line (LSRL)

Creating a LSRL

What formula do we use to find the slope?

What point does the LSRL always go through?

(x̄, ȳ)

Then fill in the equation ŷ=a+bx 

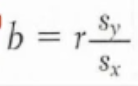
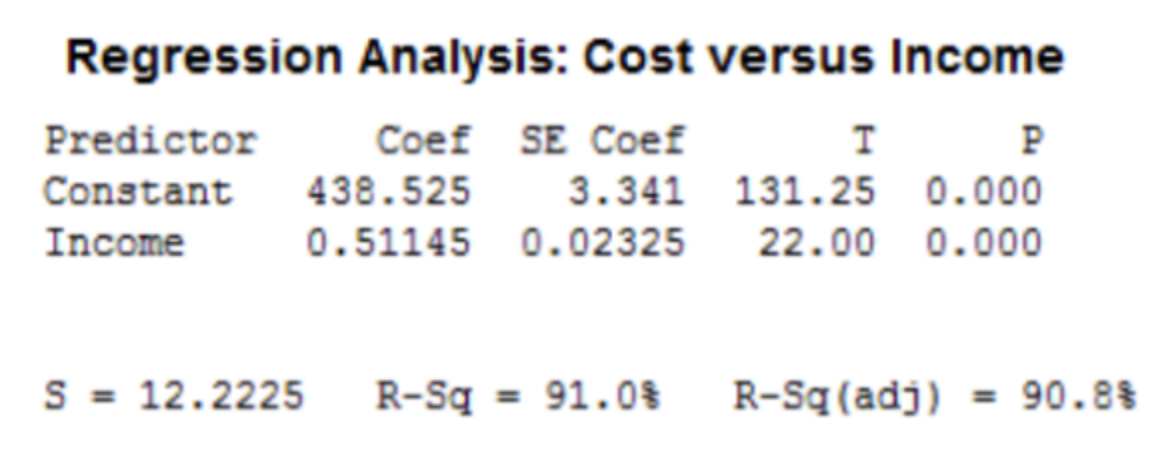
understanding regression outputs

slope =

y-int =

standard deviation of residuals =

r =

income

constant

s

√r²

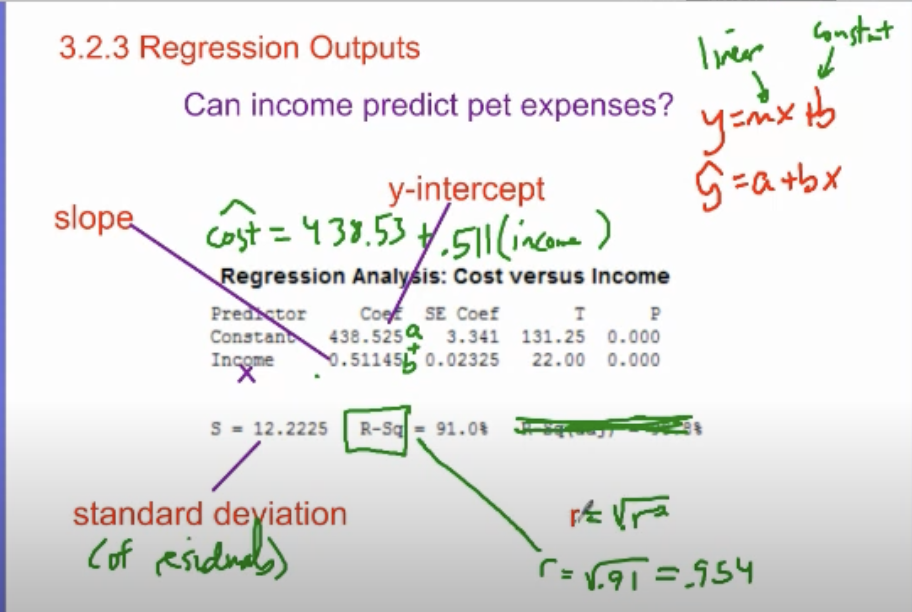
s = standard deviation of residuals

average distance from ŷ to actual y is s (units for y)

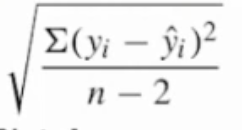
analyzing residual plot

Residual plot: The residual plot (is randomly scattered, has a pattern eg. spreading out, curved) indicating that a linear model (is, is not) appropriate.

What is your fill-in-the-blank sentence to interpret Coefficient of Determination: r²?

The % variability in [y in context] that’s accounted for by the linear model

Outliers in the y-direction (vertically far from the trend) usually:

• Increase the ____ (since they are far from the line)

• Have little effect on the ____ of the regression line if their x-value is typical

• They mostly affect the _____ strength (make r ____, i.e., weaken the linear relationship)

So: large vertical outliers make the line fit worse but don’t strongly pull it.

residual error

slope

correlation, smaller

What effect do outliers in the x-direction tend to have? What are they called?

Outliers in the x-direction are called _____ points because:

• They can strongly influence the ____ and position of the _____, sometimes pulling it toward themselves

• Removing it would noticeably change the regression line.

influential, LSRL

Not among explanatory or response variables, and yet may influence the interpretation of relationships among those variables

lurking variable

Points with large residuals are called ____ (note: the converse is not true: outliers don’t necesarily have large residuals). Points which change the slope of the line and the correlation coefficient greatly when removed are called _____

outliers,

influential points

The mean of the residuals

should be 0, if it’s not 0 means that LSRL is not perfect fit

high leverage point

far out in the x-direction

coefficient of determination

r²