Density-Dependent single population dynamics

Why is density important?

Exponential growth until limited by resource availability

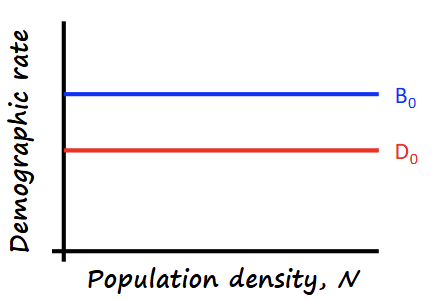
How do we model density independent per-capita birth & death rates?

B0,D0

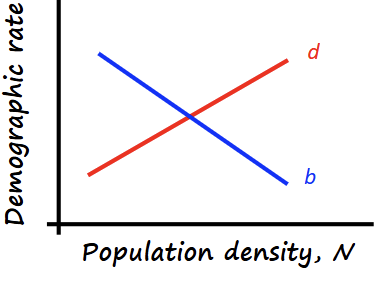
How doe we model density per-capita birth & death rates?

b,d

What does per-capita growth (pgr) mean?

Mean change in population size provided by each individual

Discrete Time Models for Exponential Growth

N_t+1=N_tR

Discrete Time Models for Generic Growth Function

N_t+1=N_tf(N_t)

Discrete Time Models for Per-capita Growth Term (Exponential)

f(N_t)=R

Discrete Time Models for Negative Density Dependence

f(N_t)=e^r(1-Nt^/K)

Continuous Time Models for Exponential Growth

dN/dt=Nr

Continuous Time Models for Generic Growth Function

dN/dt=Nf(N)

Continuous Time Models for Per-capita Growth Term

f(N)=r

Continuous Time Models for Negative Density Dependence

f(N)=r(1-N/K)

Density dependent feedback term

1-N_t/K or 1-N/K

What do state variable express & record?

The thing that is modelled

Mean field models

-State is one number

-Population density at time t

Parameters

Biological (& abiotic) elements we think affect the state variables of interest

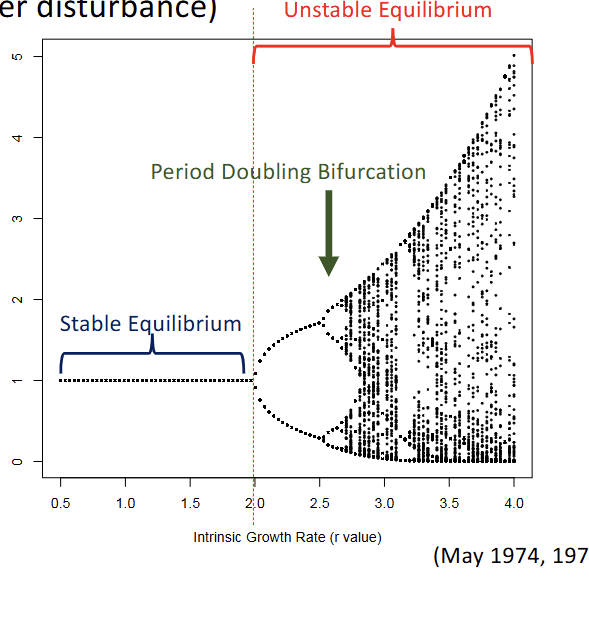
What is stability and instability?

Stability=Population return to this point after disturbance

Instability=Cycles/Chaos

Solve dN/dt=Nr(1-N/K) for N*

-Change N→N*:

dN*/dt=N*r(1-N*/K)

-Then dN*/dt=0

0=N*r(1-N/K)

-Divide by N* by both sides

0=r(1-N*/K)

-Divide by r both sides

0=1-N*/k

-Add N*/K both sides

N*/K=1

-Times N* both sides

K=N* → N*=K

Solve N_t+1=N_te^r(1-Nt/K) for N*

-Change N_t→N*:

N*=N*e^r(1-N*/K)

-Divide N* both sides

N*/N*=e^r(1-N*/K) →1=e^r(1-N*/K)

-Log both sides

log(1)=r(1-N*/K)→0=r(1-N*/K)

-Divide r both sides

0=1-N*/K

-Add N*/K both sides

N*/K=1

-Times K both sides

N*=K

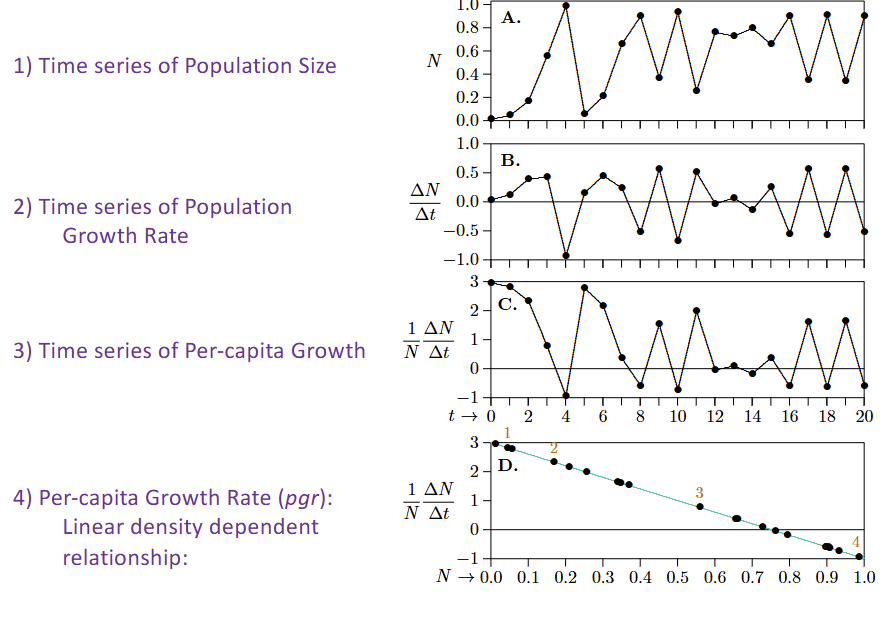
What are the ways to represent data?

-Time series of Population Size

-Time series of Population Growth Rate

-Time series of Per-capita Growth

-Per-capita Growth Rate (pgr)

Discrete time dynamics (vary carrying capacity K)

Gradual increase or decrease (N₁>K)

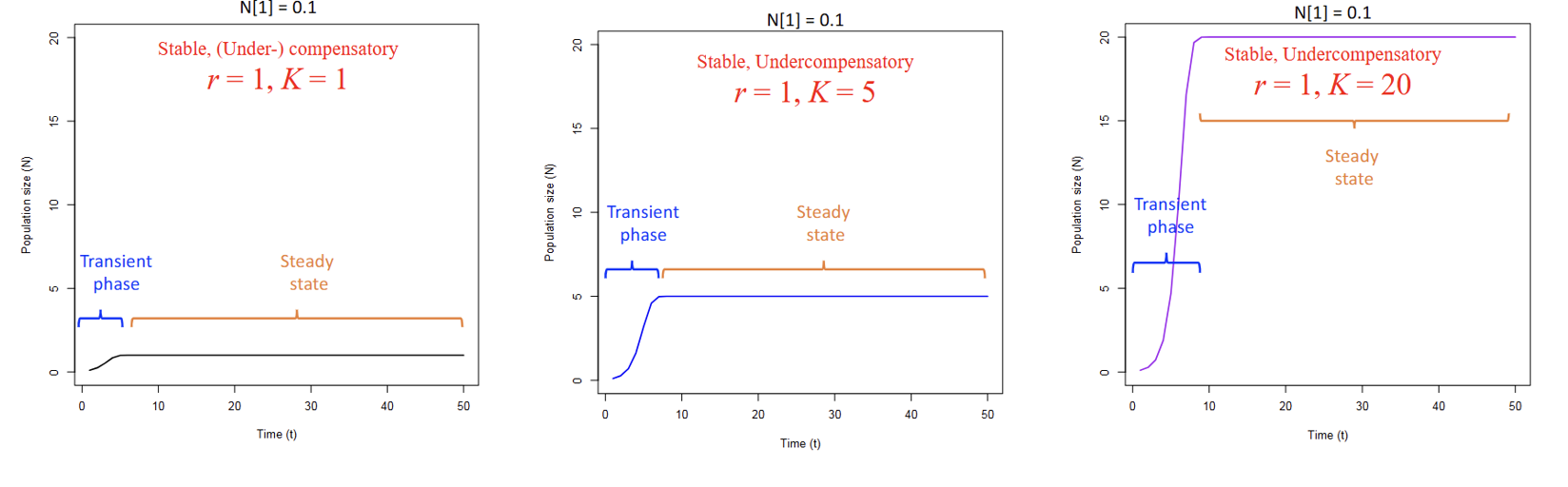
What would cause a gradual increase and a rapid decrease?

Increase=N₁<K

Decrease=N₁>K

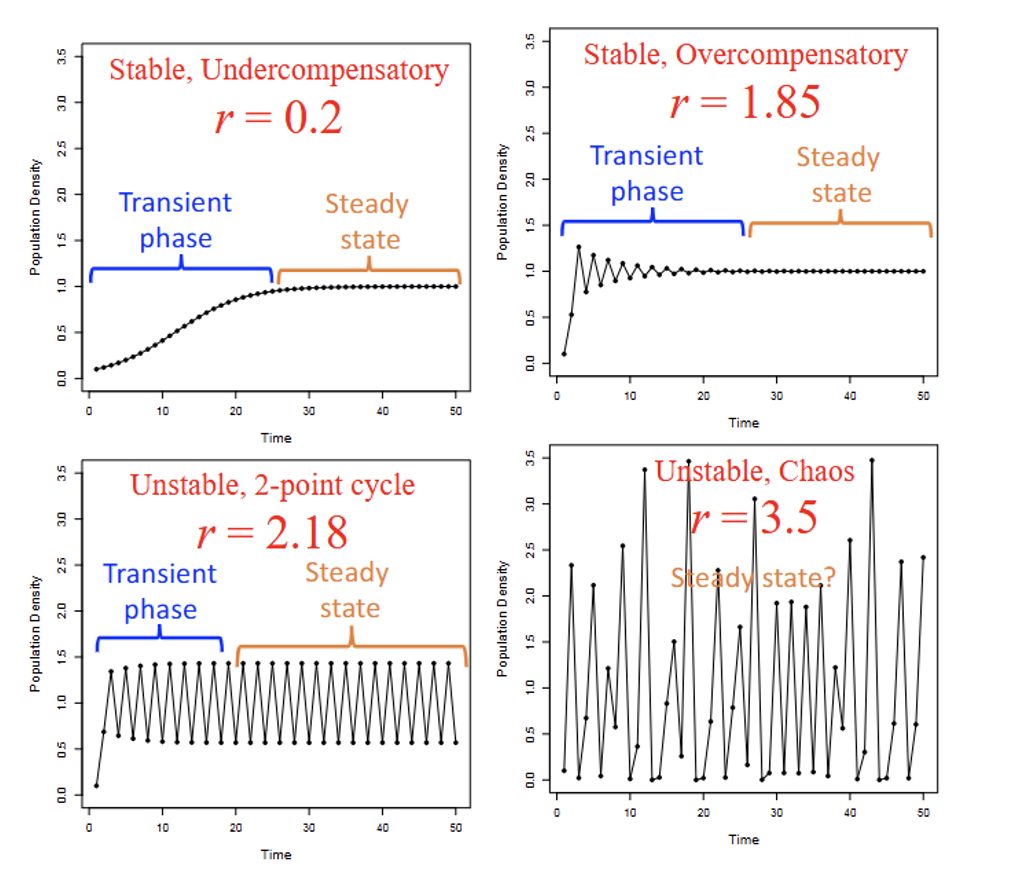
What happens if the r is increased(intrinsic growth rate)

-Approaches steady state faster

-Overshoots K

-Steady state dynamics change with r

>Stable/Cycle/Chaos

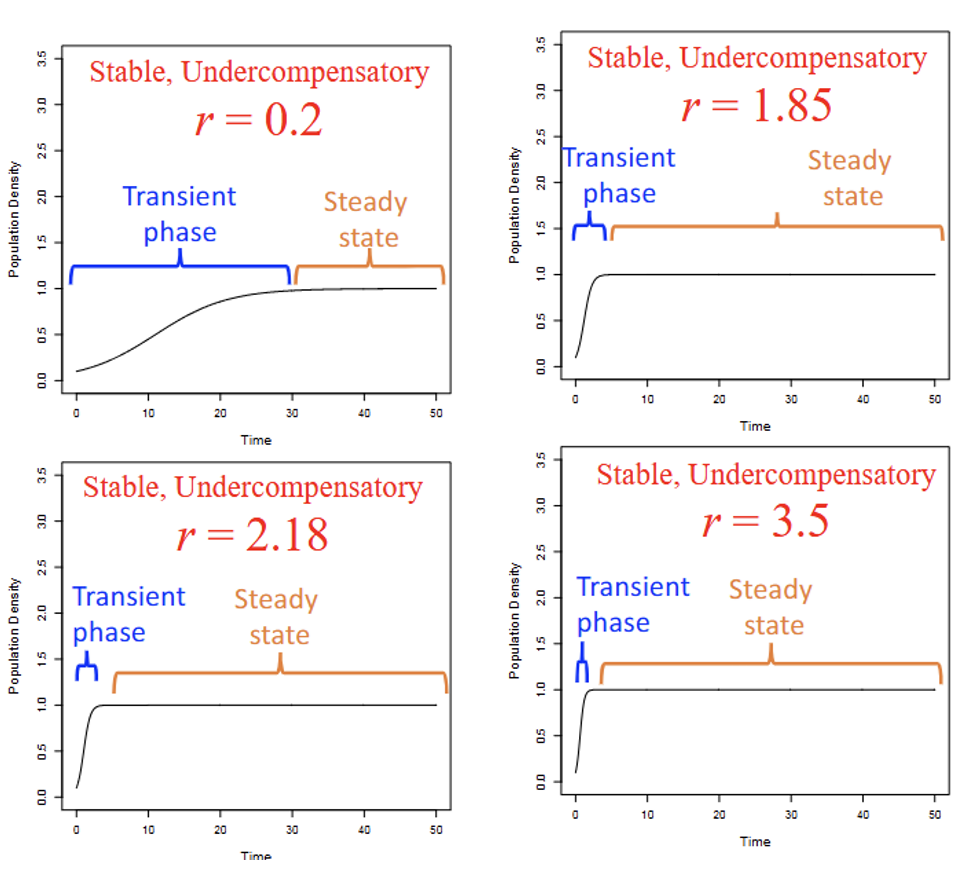
What happens if Continuous time Dynamics (dt→0) when r is increased

-Approaches steady state faster

-No change in steady state dynamics with r

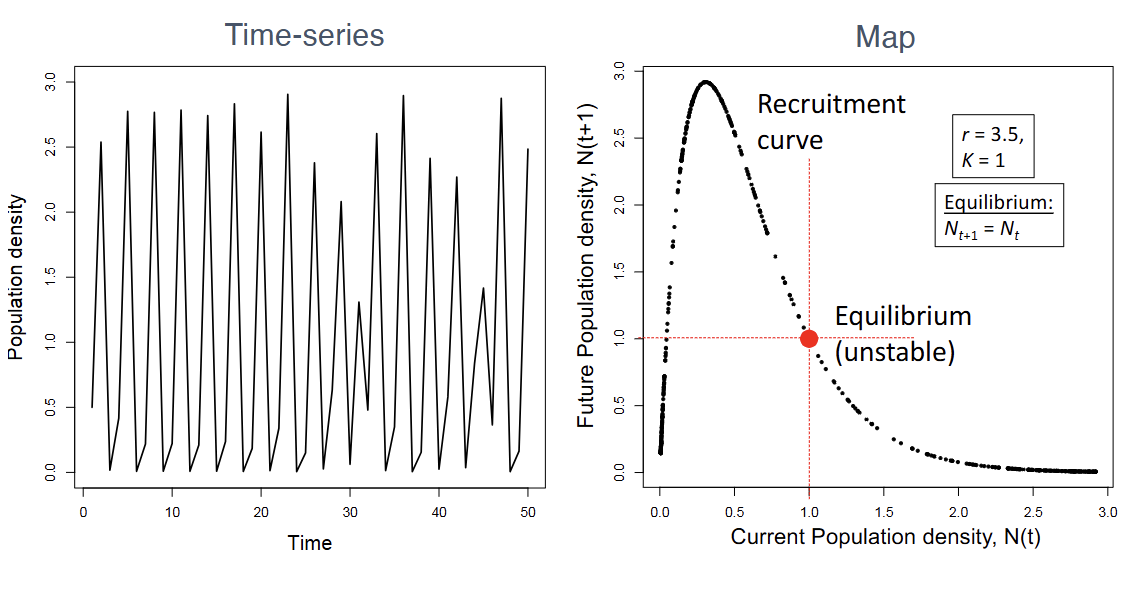
Time -Series vS Mapping Graphs

Types of bifurcation plots

-Period doubling

-Stable equilibrium to 2 points cycle

-Different point cycles

>2 to 4

>4 to 8

>8 to 16

Types of survivorship curves

k strategists

-Live to old age

-Few offspring, long parental care

Both r and K

-Constant survivorship curves

-many offspring, some parental care

R strategists

-Low early and high late survival

-Many more offspring, little or no parental care