CP5520 Final Exam: April 25th, 2025 [Duration: (1.00 am – 3.00 pm) - 2 Hour] (Hard Copy - In Class - Exam)

Total Marks: 55     Part A: 20 MCQs × 1 mark each = 20 marks     Part B: 7 Brief Answer Questions × 5 marks each = 35 marks

Which of the following is used to filter rows (tuples) based on a condition?
a) Projection (π)
b) Selection (σ)
c) Union (∪)
d) Cartesian Product (×)

b) Selection (σ)

Which operator in relational algebra returns only specific columns from a relation and removes duplicates?

a) Selection

b) Projection

c) Join

d) Division

b) Projection

What symbol is commonly used to represent the selection operator?

a) π

b) σ

c) ∪

d) ÷

b) σ

Which of the following operations is not commutative?

a) Union (∪)

b) Intersection (∩)

c) Selection (σ)

d) Set Difference (−)

d) Set Difference (−)

A natural join (⋈) is a special case of which join operation?

a) Theta join

b) Outer join

c) Division

d) Cartesian product

a) Theta join

In a join operation, which condition is used if only equality comparisons are allowed?

a) Theta–join

b) Equijoin

c) Natural join

d) Outer join

b) Equijoin

Which relational algebra operator returns those tuples in relation R that are not present in relation S?

a) Union

b) Intersection

c) Set Difference

d) Cartesian Product

c) Set Difference

The division operator (÷) is used to answer queries of the form “find all X such that X is related to all Y”.

a) True

b) False

a) True

Which property of relational algebra ensures that every operation’s result is also a relation?

a) Commutativity

b) Associativity

c) Closure

d) Idempotence

c) Closure

In tuple relational calculus, the variables range over:

a) Individual attribute values

b) Entire tuples

c) Domains of attributes

d) Relations themselves

b) Entire tuples

In domain relational calculus, the variables represent:

a) Tuples in a relation

b) Individual values from attribute domains

c) Entire relations

d) Query trees

b) Individual values from attribute domains

Which of the following quantifiers means “there exists” in relational calculus?

a) ∀

b) ∃

c) ⊕

d) ≠

b) ∃

In the expression { t | EMPLOYEE(t) ∧ t.Sal > 50000 }, the condition is analogous to which relational algebra operation?

a) Projection

b) Selection

c) Join

d) Division

b) Selection

Which operator(s) in relational algebra remove duplicate tuples in the result automatically?

a) Selection only

b) Projection only

c) Both Selection and Projection

d) Projection and all set operations like Union, Intersection

d) Projection and all set operations like Union, Intersection

The outer join operations (e.g., LEFT, RIGHT, FULL) are used to:

a) Eliminate tuples with no matching counterpart

b) Include unmatched tuples by padding with NULLs

c) Divide one relation by another

d) Project attributes from a relation

b) Include unmatched tuples by padding with NULLs

Which of the following is a valid aggregate function?

a) π

b) σ

c) AVG

d) ×

c) AVG

When performing a set union of two relations, what is a prerequisite condition?

a) Both relations must be joinable

b) Both relations must be union-compatible

c) The relations must have at least one attribute in common

d) They must have the same number of tuples

b) Both relations must be union-compatible

Which of the following operators is typically expressed as a combination of a Cartesian product and a selection?

a) Projection

b) Join

c) Division

d) Set Difference

b) Join

An attribute that uniquely identifies each tuple in a relation is known as a:

a) Super key

b) Candidate key

c) Primary key

d) All of the above

d) All of the above

What does “closure” in relational algebra mean?

a) Only one operator can be applied at a time

b) Every relational operation produces a relation that can be used as input to other operations

c) The final result always has the same schema as the original relation

d) The query terminates after one operation

b) Every relational operation produces a relation that can be used as input to other operations

Selection and Projection: Define the selection (σ) and projection (π) operators. Provide their syntaxes and explain one key property for each (e.g., commutativity for selection and the duplicate-elimination property for projection).

• Selection (σ):

  • Definition: Filters rows (tuples) from a relation based on a given predicate (condition).

  • Syntax: σ_condition(Relation) Example: σ_Salary>50000(EMPLOYEE) retrieves all employees with a salary greater than 50,000.

  • Key Property: Selection is commutative. That is, σ_condition1(σ_condition2(R)) = σ_condition2(σ_condition1(R)).

• Projection (π):

  • Definition: Extracts specific columns (attributes) from a relation, producing a relation that contains only those attributes while eliminating duplicates.

  • Syntax: π_attribute_list(Relation) Example: π_Fname, Lname(EMPLOYEE) returns the first and last names without duplicate rows.

  • Key Property: Projection automatically eliminates duplicate tuples because the result is a set.

Join Operations: Describe the differences between an equijoin, a natural join, and an outer join. Give a brief example of how each join might be used in a relational query.

• Equijoin:

  • Definition: A join where the condition consists solely of equality (e.g., R ⨝_{A = B} S).

  • Example: Joining EMPLOYEE and DEPARTMENT on the department number is an equijoin.

• Natural Join:

  • Definition: A special form of equijoin that automatically tests equality on all common attributes between the two relations and then removes duplicate columns.

  • Example: EMPLOYEE ⋈ DEPARTMENT automatically joins on the common attribute (say DNO) and projects out duplicate copies.

• Outer Join:

  • Definition: Extends the join to include unmatched tuples from one (or both) relations by padding the missing attributes with NULLs.

  • Example: A left outer join (EMPLOYEE ⟕ DEPARTMENT) returns all employees even if some have no matching department record.

Each join type is useful: equijoins for basic matching, natural joins for cleaner attribute sets, and outer joins when retaining unmatched data is required.

Division Operator: Explain the division operator (÷) in relational algebra. What type of queries is it used for? Provide a simple example query (in words or using algebraic notation) illustrating its use.

Purpose: The division operator (÷) finds all tuples in one relation (usually with attributes X ∪ Y) for which every tuple in another relation (with attributes Y) is associated.

Use Case: It is used for queries like “find all students enrolled in every course” or “retrieve employee IDs who work on every project.”

Notation and Example:

Syntax: R ÷ S

Example (word form): Given R(Student, Course) and S(Course), the query “find all students enrolled in every course” is expressed as R ÷ S. The output is the set of Student attributes for which every Course in S appears in R.

Relational Algebra vs. Relational Calculus: Compare and contrast relational algebra with relational calculus. Focus on the procedural nature of algebra versus the declarative (nonprocedural) nature of calculus.

• Relational Algebra:

  • Nature: Procedural; it specifies a sequence (or flow) of operations (such as selection, projection, join, etc.) that must be applied to obtain the result.

  • Example: Writing an expression like π_Fname, Lname(σ_Salary>50000(EMPLOYEE)) tells exactly how to retrieve employees with high salaries.

• Relational Calculus:

  • Nature: Declarative (nonprocedural); it specifies what to retrieve by describing properties that the result must have without describing how to compute it.

  • Example: The tuple relational calculus query { t.Fname, t.Lname | EMPLOYEE(t) ∧ t.Salary > 50000 } declares that you want the first and last names of employees meeting the salary condition, leaving the “how” to the system.

Both are equivalent in expressive power, but relational algebra is operational (step-by-step) while relational calculus is descriptive.

Tuple vs. Domain Relational Calculus: Define tuple relational calculus and domain relational calculus. Provide an example query from each calculus form that retrieves specific attributes from an EMPLOYEE relation.

• Tuple Relational Calculus (TRC):

  • Definition: Uses tuple variables that represent whole tuples from a relation.

  • Example Query: { t.Fname, t.Lname | EMPLOYEE(t) ∧ t.Salary > 50000 } Interpretation: “Retrieve the first and last names of every tuple t in EMPLOYEE where the salary is greater than 50000.”

• Domain Relational Calculus (DRC):

  • Definition: Uses variables that range over individual attribute values (domains).

  • Example Query: { <f, l> | ∃ s, a, … (EMPLOYEE(f, l, s, a, …) ∧ s > 50000) } Interpretation: “Retrieve the first name f and last name l from EMPLOYEE tuples where some salary s is greater than 50000.”

Both forms allow you to specify query constraints; the difference is in the granularity of the variables (entire tuples vs. individual values).

Aggregate Functions: What are aggregate functions in relational databases? Explain how aggregate functions (like COUNT, SUM, AVG, MAX, MIN) might be represented in relational algebra and discuss their importance in query processing.

Definition: Aggregate functions compute a single summary value for a group of tuples. They include COUNT, SUM, AVG, MAX, and MIN.

Representation in Relational Algebra:

Since traditional relational algebra does not include aggregates, they are often added as extended operators.

Example Notation: A grouping operator such as γ_{Deptno; COUNT(SSN), AVG(Salary)}(EMPLOYEE) This groups employees by department (Deptno) and calculates the count of employees and the average salary.

Importance: They are important for summarization and reporting tasks, such as computing the total number of employees, average salary per department, or maximum sales figures.

Set Operations and Their Properties: Discuss the set operations (union, intersection, and set difference) in relational algebra, including the concept of union compatibility. Describe their properties (such as commutativity and associativity) and note any operators that are not commutative.

• Set Operations in Relational Algebra:

  • Union (∪):

    • Definition: Combines tuples from two union-compatible relations and removes duplicates.

    • Properties: Commutative and associative.

  • Intersection (∩):

    • Definition: Returns only those tuples that appear in both relations.

    • Properties: Also commutative and associative.

  • Set Difference (−):

    • Definition: Yields tuples that are in the first relation but not in the second.

    • Properties: Not commutative; that is, in general, R − S ≠ S − R.

• Union Compatibility:

  • Two relations must have the same degree and corresponding attribute domains for these operators to apply.

These operations are foundational for combining and comparing query results.

Let R(A, B, C), S(C, D, E) be relations, and let |R| = 20 and |S| = 10. What is the maximum possible number of tuples in the relation resulting from R * S?
A. 10

B. 20

C. 30

D. 200

D. 200

Let R(A, B, C) be a relation, and let |R| = 20. What is the maximum possible number of tuples in the relation resulting from σ_A=a (R)?

A. 1

B. 10

C. 20

D. None of the others

C. 20

Let R(A, B, C) be a relation, and let |R| = 20. What is the maximum possible number of tuples in the relation resulting from σ_C=c (R)?

A. 0

B. 1

C.10

D. 20

B. 1

Let R(A, B, C, D), S(C, D, E, F, G) be relations, and let |R| = 15 and |S| = 30. What is the maximum possible number of columns in the relation resulting from R X S?

A. 7

B. 8

C. 9

D. 30

E. 450

C. 9

Let R(A, B, C,D) and S(B, C, D) be two relations. Also let |R| = 12 and |S| = 7. The resulting relation T (where T = R ÷ S):

A. Have 1 attribute and at least 1 tuple.

B. Have 3 attributes and at least 1 tuple.

C. Have 1 attribute and at most 1 tuple.

D. Have 3 attributes and at most 1 tuple.

C. Have 1 attribute and at most 1 tuple.

Let R(A, B, C), S(D, E, F) be compatible relations, and let |R| = 10 and |S| = 3. What is the maximum possible number of attributes in the relation resulting from R U S?

A. 3

B. 6

C. 10

D. 13

A. 3

Let R(A, B, C), S(D, E, F) be compatible relations, and let |R| = 10 and |S| = 25. What is the minimum possible number of attributes in the relation resulting from S - R?

A. 0

B. 10

C. 15

D. 25

C. 15

Let R(A, B, C), S(D, E, F) be compatible relations,, and let |R| = 50 and |S| = 30. What is the minimum possible number of tuples in the relation resulting from π_B,C(R U S)?

A. 0

B. 1

C. 30

D. 50

D. 50

Which one of the following statements is true?

A. Denormalization is a design decision to avoid update anomalies.

B. Normalization is to improve the performance of frequently occurring queries and transactions.

C. Normalization is to separate attributes into tables to minimize redundancy.

D. All of the others

C. Normalization is to separate attributes into tables to minimize redundancy.

Which one of the following is false?

A. Normalization is a design decision to avoid update anomalies.

B.Denormalization is to improve the performance of frequently occurring queries and transactions.

C. Normalization is to separate attributes into tables to minimize redundancy.

D. None of the others

D. None of the others

Which one of the following is NOT recomended about indexing an attribute?

A. It appears on many queries.

B. It is in a selection condition.

C. It is used for scanning values

D. It is frequently updated.

E. It is a primary key.

D. It is frequently updated.

80-20 rule means to determine the 20% least important queries.

T. True

F. False

F. False

Which one of the following does choose execution plans based on heuristically ranked operations?

A. Rule-based query optimization

B. Cost-based query optimization

C. Semantic query optimization

D. All of the others

A. Rule-based query optimization

Which one of the following is the correct order in terms of Query Optimizer?

A. Optimizing -> Parsing -> Code Generating -> Code Running

B. Optimizing -> Code Generating -> Parsing -> Code Running

C. Parsing -> Code Generating -> Optimizing -> Code Running

D. Parsing -> Optimizing -> Code Generating -> Code Running

D. Parsing -> Optimizing -> Code Generating -> Code Running

In Query Processing and Optimization, an execution plan is generated by _____.

A. the parsing phase

B. the query optimizer phase

C. the query code generator phase

D. the runtime database processor phase

B. the query optimizer phase

Which one of the following is true about external sorting?

A. All records in files are loaded and sorted in the main memory.

B. The file is sorted by external users.

C. It will sort a number of small sub-files and then merge them together.

D. The file is sorted externally.

C. It will sort a number of small sub-files and then merge them together.

In a _______, pointers to data records exist at the leaf-level nodes.

A. B-tree

B. B+-tree

B. B+-tree

Which one of the following is NOT true about clustering index?

A. The data file is ordered on a non-key field.

B. The index file is ordered on a non-key field.

C. There can be many clustering indexes on the same file.

D. None of the others

C. There can be many clustering indexes on the same file.

Which one of the following is NOT true about indexes?

A. In multilevel indexes, the original index file is called the first-level index.

B. In multilevel indexes, the top level index has all entries fit in one disk block.

C. It is possible to have many secondary indexes on the same file.

D. None of the other 3 choices

D. None of the other 3 choices

It is possible to have another secondary index on the first level of secondary index.

T. True

F. False

F. False

Let R(A, B, C) and S(B, C) be two relations. Also let |R| = 10 and |S| = 7. The resulting relation T (where T = R ÷ S):

A. Have 1 column and at least 3 tuples

B. Have 2 columns and at most 1 tuple

C. Have 2 columns and at least 2 tuples

D. Have 2 columns and at least 3 tuples

E. Have 1 column and at most 1 tuple

E. Have 1 column and at most 1 tuple

Which of the following does retrieve the first name and last name of female employees?

(a) {t | EMPLOYEE(t), t.Fname, t.Lname, t.sex = ‘F’}

(b) {t.Fname, t.Lname | EMPLOYEE(t), t.sex = ‘F’}

(c) {t.Fname, t.Lname, t.sex = ‘F’| EMPLOYEE(t) }

(d) {t.Fname, t.Lname | EMPLOYEE(t) AND t.sex = ‘F’}

(e) None of the above.

(d) {t.Fname, t.Lname | EMPLOYEE(t) AND t.sex = ‘F’}

Let R(A, B, C) be a relation, and let |R| = 20. What is the maximum possible number of tuples in the relation resulting from C=c (R)?

(a) 20

(b) 1

(c) 0

(d) None of the above.

(b) 1

Let R(A, B, C) be a relation, and let |R| = 20. What is the minimum possible number of tuples in the relation resulting from πA, B (R)?

(a) 20

(b) 1

(c) 0

(d) None of the above.

(b) 1

Which of the following retrieves the address of all employees who work for the ‘Research’ department?

(a) {t.ADDRESS | EMPLOYEE(t) AND (d) (DEPARTMENT(d) AND d.DNAME='Research' AND d.DNUMBER=t.DNO)}

(b) {t.ADDRESS | EMPLOYEE(t) AND (d) (DEPARTMENT(d) AND d.DNAME='Research' AND d.DNUMBER=t.DNO)}

(c) {t.ADDRESS | EMPLOYEE(t) AND (d) (NOT DEPARTMENT(d) OR d.DNAME='Research' AND d.DNUMBER=t.DNO)}

(d) None of the above.

(b) {t.ADDRESS | EMPLOYEE(t) AND (d) (DEPARTMENT(d) AND d.DNAME='Research' AND d.DNUMBER=t.DNO)}

Use the following schema for this question.

Write a relational algebra to retrieves the first name, last name, and salary of all employees who work in department number 1.

π_{FName, LName,} Salary(σ_Dno=1(EMPLOYEE))

Use the following schema for this question.

Write a relational algebra to retrieve the first name and last name of all employees who work for the ‘Research’ department.

π_{FName, LName}(σ_{Dname=’Research’}(DEPARTMENT⨝ _Dnumber=Dno EMPLOYEE))

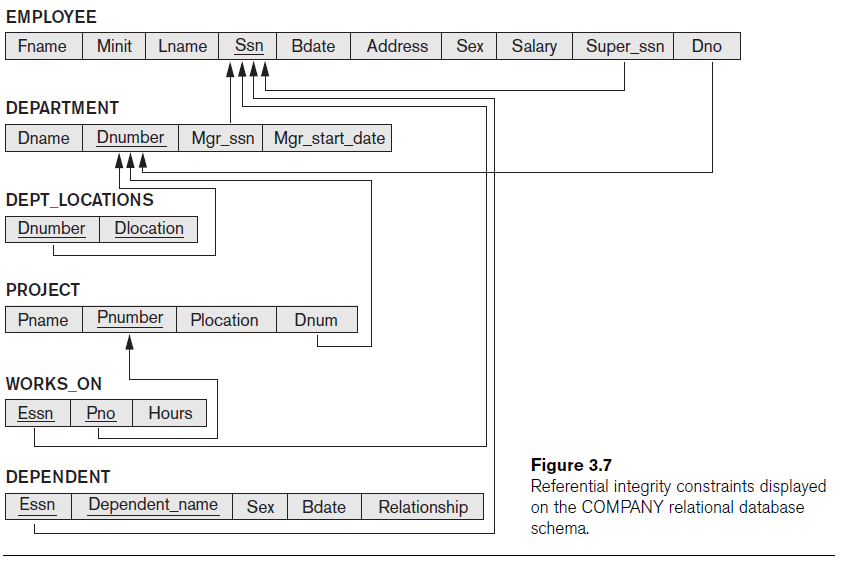
Use the following schema for this question.

Write a relational algebra to retrieve the first name and last name of all employees who work on the project “Reorganization”.

Choice 1:

π_{Fname, Lname}( EMPLOYEE ⨝_Ssn=Essn(σ_{Pname=’Reorganization’} (PROJECT ⨝_Pnumber=Pno WORKS_ON)) )

Choice 2:

REORGANIZATION_PNO ← π_Pnumber(σ_{Pname=’Reorganization’} PROJECT))
ESSNs ← π_Essn(WORKS_ON ⨝_Pno=Pnumber REORGANIZATION_PNO)
RESULT ← π_{Fname, Lname}(EMPLOYEE _Ssn=Essn ESSNs)

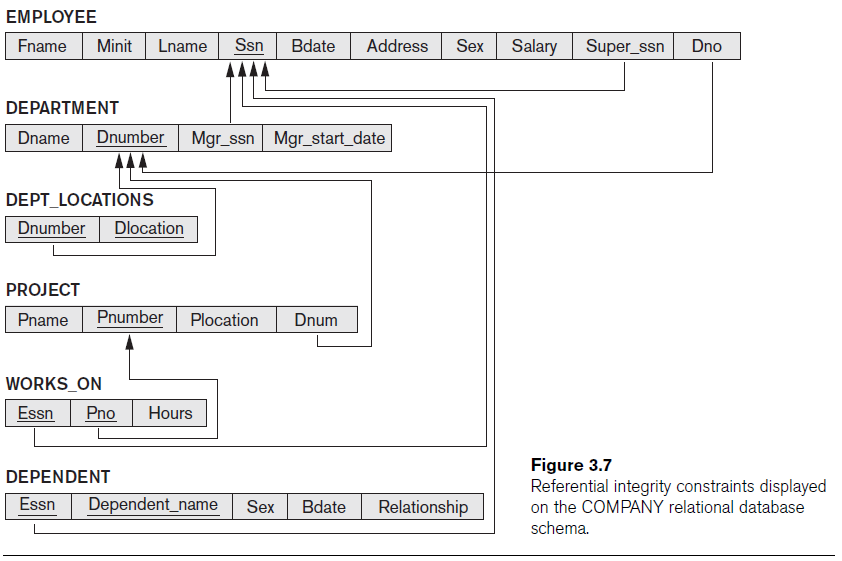
Use the following schema for this question.

Write a relational algebra to retrieve the first name and last name of all employees who do not work on any project.

WORKS_ON_ESSN ← π_Essn(WORKS_ON)

EMPLOYEE_SSN ← π_Ssn(EMPLOYEE)

NO_PROJECT_SSN ← EMPLOYEE_SSN - WORKS_ON_ESSN

RESULT ← π_{Fname, Lname}(EMPLOYEE * NO_PROJECT_SSN)

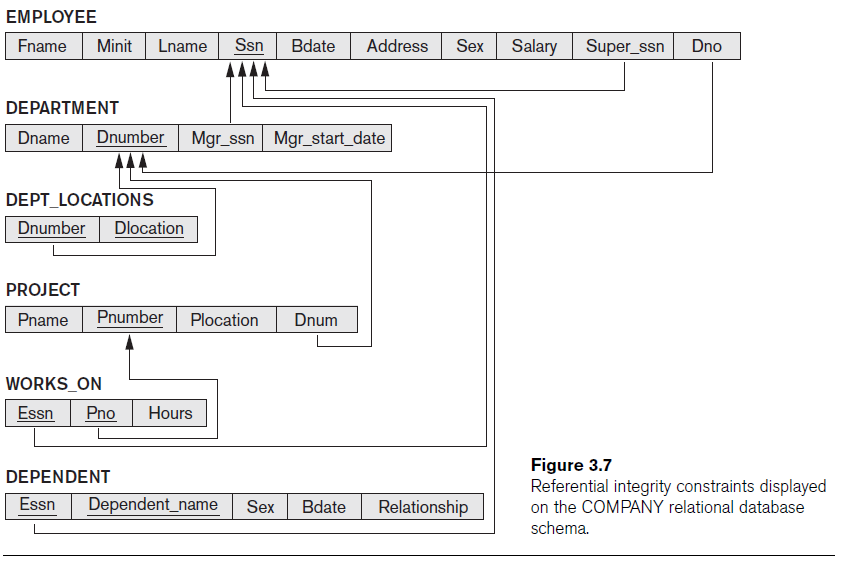
Use the following schema for this question.

Write a relational algebra to retrieve the first name and last name of all employees who work on every project.

ALL_PNO ← π_Pnumber(PROJECT)

WORK_ALL_ESSNs ← π_Essn(WORKS_ON ÷ ALL_PNO)

RESULT ← π_{Fname, Lname}(EMPLOYEE ⨝_Ssn=Essn WORK_ALL_ESSNs)

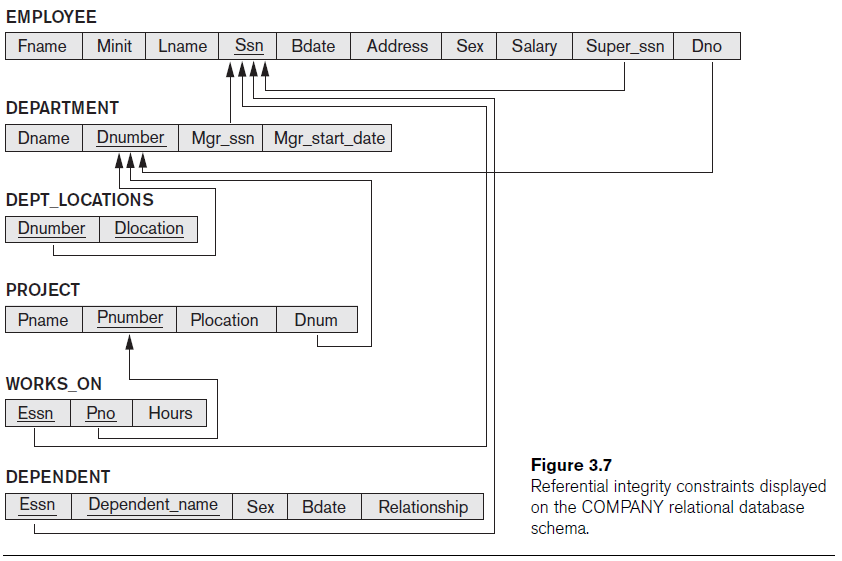
Use the following schema for this question.

Write a relational algebra to retrieve the average salary of all female employees.

FEMALEs ← σ_{Sex=’female’}(EMPLOYEE)

RESULT ← Ƒ_{AVG Salary}(FEMALEs)

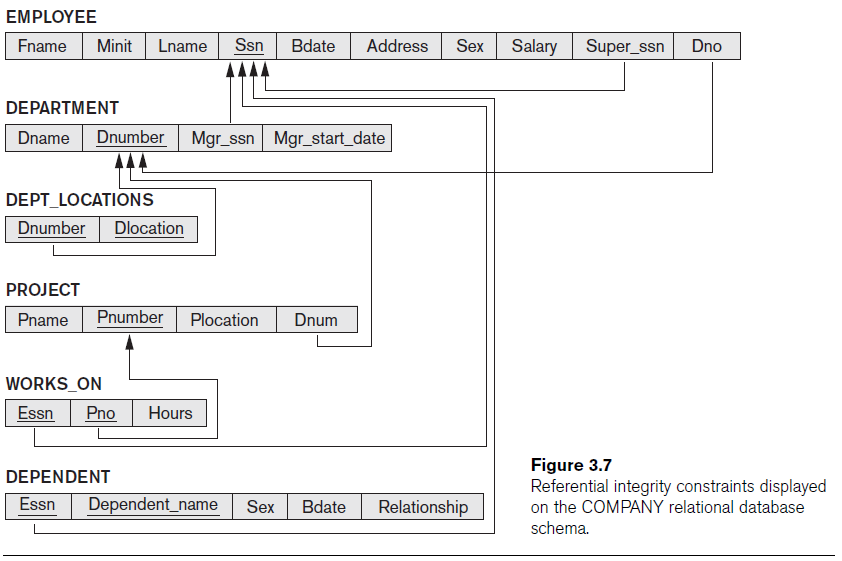
Use the following schema for this question.

Write a relational algebra to do the following:

For each department, retrieve the department name, and the average salary of employees working in that department.

DEP_AVG_SAL (Dno, Average_salary) ← _DnoƑ_{AVG Salary}(FEMALEs)

RESULT ← π_{Dname, Average_salary}(DEPARTMENT ⨝_Dnumber=Dno DEP_AVG_SAL)

True or False:

In multilevel indexes, the original index file is called the first-level index.

True

True or False:

In multilevel indexes, the top level index has all entries fit in one disk block.

True

True or False:

It is possible to have many clustering indexes on the same file.

False

True or False:

It is possible to have a multilevel index for any type of first-level index (primary, secondary and clustering).

True

True or False:

It is possible to have another secondary index on the first-level index file.

False

True or False:

Secondary indexes are non-dense indexes.

False

True or False:

We cannot have both primary index and secondary index on the same file.

False

Which of the following is more appropriate when using clustering indexes?

A. The data file is ordered on a non-key field but the index file is not.

B. The index file is ordered on a non-key field but the data file is not.

C. Both the index file and the data files are ordered on a non-key field.

D. Neither the data file nor the index file is ordered on a non-key field.

E. None of the above.

C. Both the index file and the data files are ordered on a non-key field.

Use the following description of a disk for this question.

Suppose that a disk unit has the block size 512 bytes. Assume that we use the unspanned approach to store a file that has 20000 student records of fixed length, where the record size is 120 bytes.

The blocking factor is:

A. [520 /120]

B. [20000 /512]

C. [512 /120]

D. [20000 /512]

E. 20 + 10 + 1

C. [512 /120]

Use the following description of a disk for this question.

Suppose that a disk unit has the block size 512 bytes. Assume that we use the unspanned approach to store a file that has 20000 student records of fixed length, where the record size is 120 bytes.

The wasted space in each disk block because of the unspanned organisation is:

A. 1 byte.

B. 10 bytes.

C. 20 bytes.

D. 32 bytes.

E. 120 bytes.

D. 32 bytes.

Use the following description for this question.

Suppose we have an ordered file with 1000 records of fixed length (each record 100 bytes). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes. Assume that the ordering key field of the file is K = 14 bytes long, a block pointer is P = 6 bytes long, and we have constructed a primary index for the file.

The blocking factor is:

A. 5

B. 6

C. 20

D. 512

E. 1000

A. 5

Use the following description for this question.

Suppose we have an ordered file with 1000 records of fixed length (each record 100 bytes). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes. Assume that the ordering key field of the file is K = 14 bytes long, a block pointer is P = 6 bytes long, and we have constructed a primary index for the file.

The number of disk blocks to store the file:

A. 14

B. 100

C. 200

D. 512

E. 1000

C. 200

Use the following description for this question.

Suppose we have an ordered file with 1000 records of fixed length (each record 100 bytes). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes. Assume that the ordering key field of the file is K = 14 bytes long, a block pointer is P = 6 bytes long, and we have constructed a primary index for the file.

The number of records (or entries) in the first level of the index file is:

A. 100

B. 200

D. 300

E. 1000

B. 200

Use the following description for this question.

Suppose we have an ordered file with 1000 records of fixed length (each record 100 bytes). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes. Assume that the ordering key field of the file is K = 14 bytes long, a block pointer is P = 6 bytes long, and we have constructed a primary index for the file.

The record size of each entry of the index file is:

A. 6 bytes.

B. 14 bytes.

C. 512 + 6 (i.e. 518) bytes.

D. 14 + 6 (i.e. 20) bytes.

E. 512 + 14 + 6 (i.e. 532) bytes.

D. 14 + 6 (i.e. 20) bytes.

Use the following description for this question.

Suppose we have an ordered file with 1000 records of fixed length (each record 100 bytes). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes. Assume that the ordering key field of the file is K = 14 bytes long, a block pointer is P = 6 bytes long, and we have constructed a primary index for the file.

The index blocking factor:

A. 8

B. 9

C. 10

D. 14

E. 25

E. 25

Use the following description for this question.

Suppose we have an ordered file with 1000 records of fixed length (each record 100 bytes). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes. Assume that the ordering key field of the file is K = 14 bytes long, a block pointer is P = 6 bytes long, and we have constructed a primary index for the file.

The number of disk blocks required to store the entries of the first level of the index file is:

A. 8

B. 9

C. 10

D. 14

E. 25

A. 8

Use the following information for this question.

Consider a disk with block size 512 bytes. We wish to store a file that has 5000 student records of fixedlength (each record is 100 bytes long) on the disk using contiguous allocation with unspanned organisation. Suppose that we have constructed a secondary index on a 7-byte-non-ordering field of the file with the record pointer size of 8 bytes.

The blocking factor is:

(a) 5

(b) 6

(c) 7

(d) 8

(e) 9

(a) 5

Use the following information for this question.

Consider a disk with block size 512 bytes. We wish to store a file that has 5000 student records of fixedlength (each record is 100 bytes long) on the disk using contiguous allocation with unspanned organisation. Suppose that we have constructed a secondary index on a 7-byte-non-ordering field of the file with the record pointer size of 8 bytes.

The number of disk blocks needed to store the file is:

(a) 100 disk blocks

(b) 200 disk blocks

(c) 400 disk blocks

(d) 800 disk blocks

(e) 1000 disk blocks

(e) 1000 disk blocks

Use the following information for this question.

Consider a disk with block size 512 bytes. We wish to store a file that has 5000 student records of fixedlength (each record is 100 bytes long) on the disk using contiguous allocation with unspanned organisation. Suppose that we have constructed a secondary index on a 7-byte-non-ordering field of the file with the record pointer size of 8 bytes.

The index blocking factor is:

(a) 15

(b) 30

(c) 34

(d) 68

(e) 100

(c) 34

Use the following information for this question.

Consider a disk with block size 512 bytes. We wish to store a file that has 5000 student records of fixedlength (each record is 100 bytes long) on the disk using contiguous allocation with unspanned organisation. Suppose that we have constructed a secondary index on a 7-byte-non-ordering field of the file with the record pointer size of 8 bytes.

The number of disk blocks required to store the entries of the index file is:

(a) 147 disk blocks

(b) 148 disk blocks

(c) 512 disk blocks

(d) 513 disk blocks

(e) 1000 disk blocks

(b) 148 disk blocks

Use the following information for this question.

Consider a disk with block size 512 bytes. We wish to store a file that has 5000 student records of fixedlength (each record is 100 bytes long) on the disk using contiguous allocation with unspanned organisation. Suppose that we have constructed a secondary index on a 7-byte-non-ordering field of the file with the record pointer size of 8 bytes.

Suppose that the secondary index is converted into a multilevel index, the top level of the index is:

(a) 1

(b) 2

(c) 3

(d) 4

(e) 5

(c) 3

Use the following description for this question.

Suppose we have a file with 200 records of fixed length (each record 120 bytes). The non-key attribute, DNO, has 10 distinct values and all records are evenly distributed based on the DNO value (i.e. each cluster has 200/10 = 20 members). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes.

Assume that the ordering non-key field of the file (i.e. the DNO attribute) is K = 4 bytes long, a block pointer is P = 6 bytes long, and we have constructed a clustering index for the file.

The number of disk blocks that are required to store this file is:

A. 20

B. 50

C. 54

D. 100

E. 120

B. 50

Use the following description for this question.

Suppose we have a file with 200 records of fixed length (each record 120 bytes). The non-key attribute, DNO, has 10 distinct values and all records are evenly distributed based on the DNO value (i.e. each cluster has 200/10 = 20 members). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes.

Assume that the ordering non-key field of the file (i.e. the DNO attribute) is K = 4 bytes long, a block pointer is P = 6 bytes long, and we have constructed a clustering index for the file.

Using a separate block cluster for each group, the number of disk blocks needed to store this file is:

A. 50

B. 54

C. 70

D. 100

E. 120

A. 50

Use the following description for this question.

Suppose we have a file with 200 records of fixed length (each record 120 bytes). The non-key attribute, DNO, has 10 distinct values and all records are evenly distributed based on the DNO value (i.e. each cluster has 200/10 = 20 members). This file is stored in a disk (using contiguous allocation with unspanned organization) where capacity of each block of the disk is 512 bytes.

Assume that the ordering non-key field of the file (i.e. the DNO attribute) is K = 4 bytes long, a block pointer is P = 6 bytes long, and we have constructed a clustering index for the file.

The number of entries/records in the first level of the index file is:

A. 10

B. 20

C. 120

D. 200

E. 512

A. 10

In a B⁺ -Tree of order p:

A. Each internal node has at most ⎡p / 2⎤ tree pointers.

B. Each internal node, except the root, has at least ⎡p / 2⎤ tree pointers.

C. An internal node with q tree pointers, q ≤ p, has q − 1 search field values.

D. Both B. and C. are correct.

E. None of the above.

D. Both B. and C. are correct.

Which of the following is true?

In a B⁺-tree of order p, each internal node has:

(a) at most p node pointer and p key values.

(b) at most p node pointers and p - 1 key values.

(c) at most p - 1 node pointers and p key values.

(d) at most p - 1 node pointers and p - 1 key values.

(e) at most p/2 node pointers and p - 1 key values.

(b) at most p node pointers and p - 1 key values.

In a , pointers to data records exist at all levels of the tree.

A. B-tree

B. B⁺-tree

A. B-tree

Which one of the following steps of processing a high-level query is to produce an execution plan?

A. Scanning, parsing, and validating

B. Query optimizer

C. Query code generator

D. Runtime database processor

E. None of the above.

B. Query optimizer

Which of the following is the correct order in terms of Query Optimizer?

A. Parsing 🡺 Code Generating 🡺Optimizing 🡺 Code Running

B. Optimizing 🡺Parsing 🡺Code Generating 🡺 Code Running

C. Parsing 🡺 Optimizing 🡺Code Generating 🡺 Code Running

D. Optimizing 🡺 Code Generating 🡺 Parsing 🡺 Code Running

E. None of the above

C. Parsing 🡺 Optimizing 🡺Code Generating 🡺 Code Running

Use the following description (in regard to external sorting) for this question.

Suppose that the available buffer space is 10 blocks, and a file has 97 blocks of data.

The number of initial runs in sorting phase is:

A. 5

B. 7

C. 8

D. 10

E. 74

D. 10

Use the following description (in regard to external sorting) for this question.

Suppose that the available buffer space is 10 blocks, and a file has 97 blocks of data.

The number of passes in merging phase is:

A. 1

B. 2

C. 3

D. 10

E. 74

B. 2

External sorting refers to sorting algorithms that are suitable for .

(a) long transactions

(b) small files of records

(c) large files of records

(d) external files

(e) external users

(c) large files of records

Brute Force search is another term of .

(a) Linear search

(b) Binary search

(c) Uniform search

(d) Quick search

(a) Linear search

In query optimization, the main heuristic is .

(a) to apply binary operations such as JOIN or UNION before unary operations such as SELECT or PROJECT

(b) to reduce the size of intermediate results

(c) to eliminate duplicated values

(d) to minimize data redundancy

(b) to reduce the size of intermediate results

Which of the following is the most expensive operation?

(a) JOIN

(b) CARTESIAN PRODUCT

(c) SELECT

(d) PROJECT

(b) CARTESIAN PRODUCT

What cost component is the most concerned cost for distributed database systems in terms of cost-based query optimization?

(a) Access cost to secondary storage

(b) Storage cost

(c) Computation cost

(d) Memory usage cost

(e) Communication cost

(e) Communication cost

Which of the following does use constraints specified on the database schema for query optimization?

(a) Rule-based query optimization

(b) Cost-based query optimization

(c) Semantic query optimization

(d) All of the above

(c) Semantic query optimization

A PARTS file with Part# as the key field includes records with the following Part# values: 1, 18, 9, 20, 3,12. Suppose that the search field values are inserted in the given order in a B⁺-tree of order p = 3 and p_leaf = 2.

(a) Show how the tree will expand and what the final tree will look like.

(b) Delete the following values: 20, 18, 12 and 3. Show how the tree will shrink (in the given order) and show the final tree.

Please check with “Question 14” of Page 25 from “1 to 8 questions + solutions.pdf”

What are the differences among primary, secondary, and clustering indexes?

How do these differences affect the ways in which these indexes are implemented?

Which of the indexes are dense, and which are not?

In primary indexes, the data file is ordered on a key field.

In secondary indexes, the data file may not be ordered.

In clustering indexes, the data file is ordered on a non-key field.

• All of these index files (i.e., primary, secondary, and clustering indexes) are ordered files, and have two fields of fixed length. One field contains data (in which its value is the same as a field from data file) and the other field is a pointer to the data file, but:

• In primary indexes, the data item of the index has the value of the primary key of the first record (the anchor record) of the block in which the pointer points to.

• In secondary indexes, the data item of the index has a value of the secondary key and the pointer

• points to a block, in which a record with such secondary key is stored.

• In clustering indexes, the data item on the index has a value of the non-key field, and the pointer points to the block in which the first record with such non-key field is stored in.

• In primary index files, corresponding to each block in a data file, one record exists in the

primary index file. That is, the number of records in the index file is equal to the number of blocks in the data file. Hence, the primary indexes are not dense.

• In secondary index files, corresponding to each record in the data file, one record exists in the secondary index file. That is, the number of records in the secondary index is equal to the number of records in the data file. Hence, the secondary indexes are dense.

• In clustering index files, corresponding to each distinct clustering field, one record exists in the clustering index file. That is, the number of records in the clustering index is equal to the number of distinct clusters of the clustering field. Hence, the clustering indexes are not dense.

Why can we have at most one primary or clustering index on a file, but several secondary indexes?

The primary and clustering indexes require that the data file be ordered on a primary key or a clustering field. A filecannot be ordered on more than one field. Therefore, we cannot have more than one primary or clustering index on a file. But in secondary indexes, the file is not ordered and thus, we can have more than one secondary index on the

file.

What is the order of n of a B-tree? What is the order n of a B+-tree? List 2 similarities and 2 differences between B-tree and B⁺-tree.

The order of n in a B-tree is the number of tree pointers in each node. This number, n, is one more than the number of data items that can be stored in a node. That is, in a B-tree of order n, each node contains at most n tree pointers and n - 1 data pointers.

The order of n in a B⁺-tree is the number of tree pointers in each node. This number, n, is one more than the number of search keys that can be stored in a node. That is, in a B⁺-tree of order n, each internal node contains at most n tree pointers and n - 1 search keys. Note that in a B⁺-tree the structure of internal and leaf nodes are different.

Similarities:

- Each node, except the root and leaf nodes, has at least [𝑛/2] tree pointers.

- Each node contains at most n-1 search key values; n is the order of the tree.

- A node with m tree pointer (m ≤ n) has m - 1 search key values; n is the order of the tree.

Differences:

- Whereas in a B-tree, pointers to data records exist at all levels of the tree; in a B+-tree, all pointers to data records exists at the leaf-level nodes.

- A B⁺-tree can have less levels (or higher capacity of search values) than the corresponding B-tree.