5) Groundwater flow and darcy's law

what did darcy observe in his constant head experiments

Q (flow=volume per unit time) is proportional to ∆h across the cylinder

water moves from high head to low head

Q is proportional to properties of sand used (coarse, fine)

Q is proportional to the cross-sectional area of the cylinder

what is important about Q

and q?

what is the slope in a q vs ∆h/L plot?

Q is proportional to hydraulic gradient times area

q = Q/A = specific discharge or darcy flux
units are L/T (m/s), but it’s not a velocity, it’s volume per time*area

the slope in a q vs ∆h/L plot is K (hydraulic conductivity)

what is darcy’s law in words?

the rate water discharge through a given surface area depends on the hydraulic gradient, and on the ability of the porous medium to transmit water (hydraulic conductivity)

greater force applied on water (higher hydraulic gradient) and easier for water to pass through porous medium (higher hydraulic conductivity), the more water can be transmitted

why the negative sign in darcy’s law?

flow is in the direction of maximum rate of change of decreasing head

K cannot be negative, the negative sign indicates that water moves from high to low head

what are the two key components of darcy’s law

hydraulic gradient: ∆h/∆L, represents driving force behind flow, unitless

hydraulic conductivity: K, proportionality constant related to the properties of the fluid and porous medium, the ease with which water well pass through a particular porous medium
K is larger for coarse-grained materials and smaller for fine-grained materials
units of L/T (not a velocity)

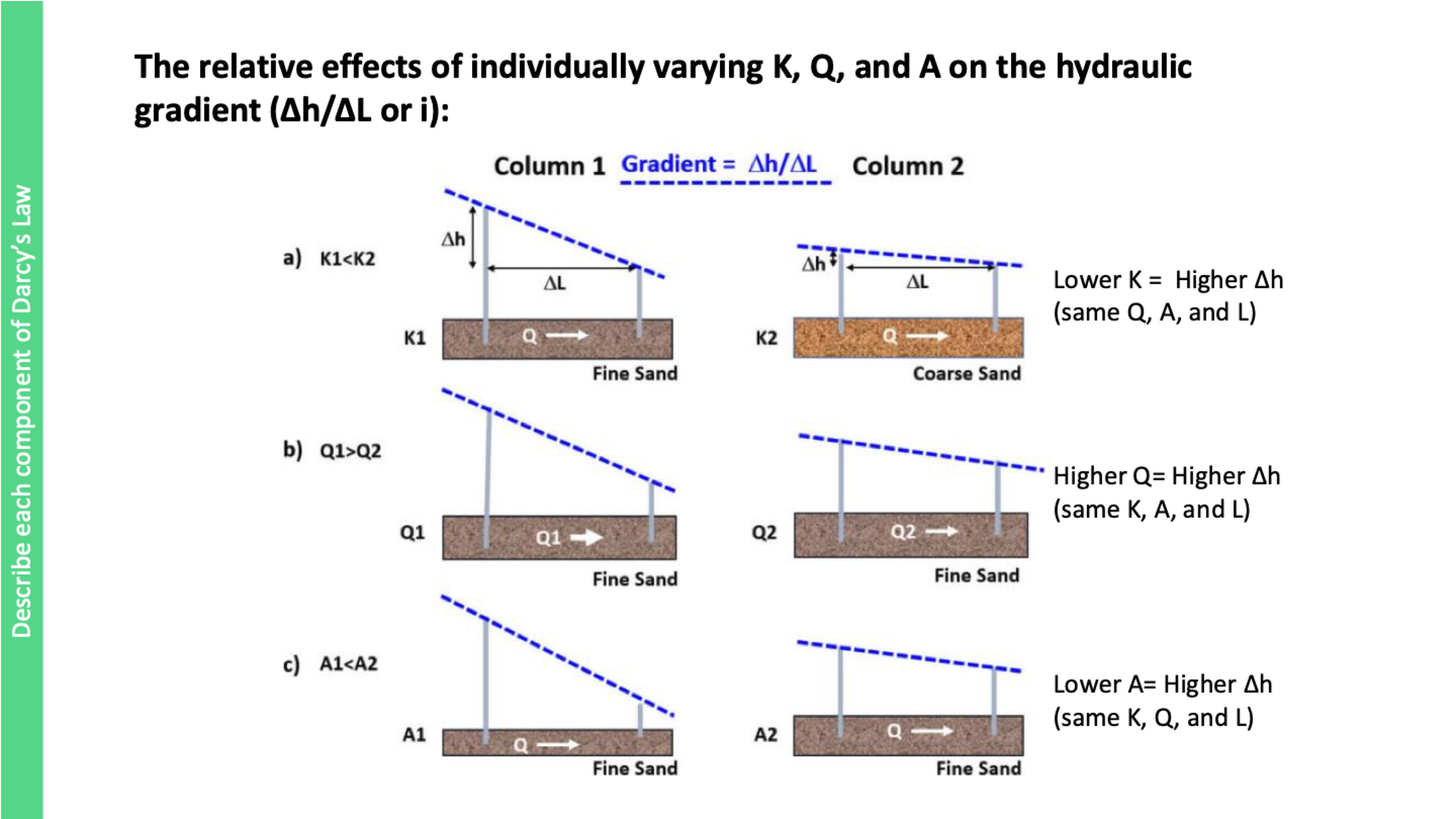
explain this

‘a) K1 is less than K2, which causes a higher hydraulic gradient (harder for water to pass through, more pressure causing higher head)

‘b) Q1 is more than Q2, higher hydraulic gradient (more pressure causing higher head)

‘c) A1 is less than A2, higher hydraulic gradient, more pressure from smaller area causing higher head)

explain transient changes in gradients

when would we need to assume transient?

rate of flow changes 

often assumed steady state for simplicity

when aquifer boundaries are changing, or there is fluctuating recharge

what does average groundwater velocity mean?

actual travel length of water through particlse is greater than straight line distance. water follows torurous path around soil grains

slower velocities nearby grains due to friction

need to average over REV

important info on clay in relation to groundwater flow

best to not assume all pores are connected

clay’s intrinsic porosity is much higher than it’s effective porosity

how does darcy flux compare to GW velocity?

imagine hose with water flowing through

2 situations both have the same flux. water with no obstruction has lower velocity than putting thumb over. The time to fill a bucket with that hose is the same even with different velocities

what is K

hydraulic conductivity: the ease at which a fluid can flow through a medium
not a velocity, but units m/s
K is a function of both the porous medium and the fluid passing through it

on a flux vs hydraulic gradient plot, K is the slope

what is K controlled by?

intrinsic permeability: related to porous media

fluid flow properties: viscosity, fluid density

solid geometric properties: pore diameter, shape of pores

‘k vs K

‘k: permeability
how easily a porous medium can transmit liquid, units m² or darcys
depends on properties of the poroud medium
is independent of the nature of the liquid or potential field

K: hydraulic conductivity
coefficient of proportionality describing the rate at which water can move through a permeable medium, units m/s
depends on materials permeability, fluid density, and viscosity

what is K for some geologic materials

gravel: 10^2-10^6

silty sand: 10^-2 - 10^2

glacial till: 10^-7 - 10^-1

T/F a high porosity corresponds with a high K

generally yes, but not for clay

must take into account pore size distribution and how easy it is to drain water out of pores

how is K propotional to Cd²

doubling grain size diameter (d) doubles pore diameter, increasing K
Increased pore size reduced tortuosity
more pores = greater tortuosity = lower K

what are ways to measure hydraulic conductivity

visual correlation: pick literature value based on sediment type

grain size methods: only suitable for coarse grains (d10=0.1-3mm) (0.001-0.1L)

permeameter tests: constant or falling head (0.01-1L)

single-well tests: slug or bail tests (1-100L)
pumping tests: force a change in hydraulic head by pumping water from the ground, measure recovery of water level to initial value over time (1000+ L)

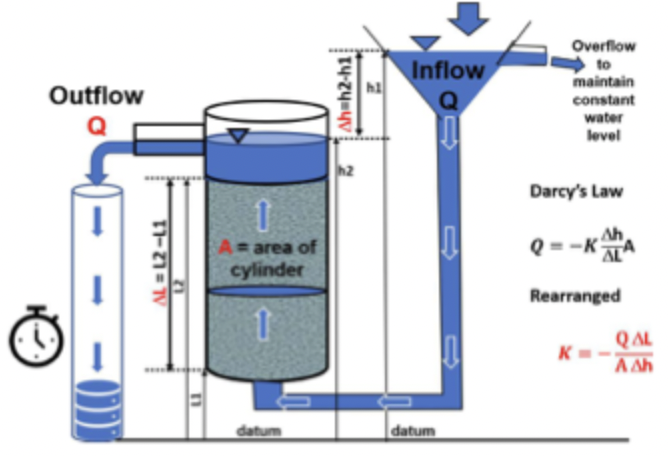
details on constant head test

constant flow of water (Q) and constant hydraulic gradient using overflow

steady state

measure Q and compute K using darcy’s law

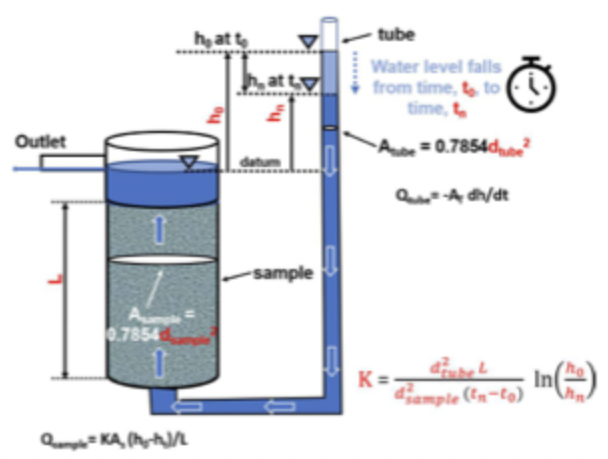
details on falling head test

better for when K is low

water levels and flow rates change over time
need sample dimensions, connected tube and the change in water level over time

take measurements in established intervals of time

K is (cross sectional area of tube/crosssectional area of soil sample) (length / ∆t) * ln(h0/h1)

what are limitations of darcy’s law

it fails when kinetic energy becomes significant compared to frictional heat loss
only works with laminar flow

examples of hydraulic gradient errors in darcys law, measurements in

water levels in closely spaced wells with nearly identical hydraulic heads

highly permeable sediments

wells with differing screen lengths intersecting geologic units in poor hydraulic connection

wells that are not hydraulically connected to each other due to geological barriers or clogged well screens

wells intersecting zones containing waters of different density (dissolved solids)