IADS Sem 1

What are algorithms?

What are algorithms?

Methods or recipes for solving various problems

What are data structures?

Ways of storing or representing data that make it easy to manipulate

What is divide-conquer-combine?

Algorithm design paradigm that breaks a problem into smaller subproblems, solves them recursively, and then combines the solutions.

What is the pseudocode for binary search?

What does O(log n) imply?

logarithmic time: the algorithm doesn’t even read the whole input

What does O(n) imply?

linear time: the algorithm accesses the input only a constant number of times

What does O(n log n) imply?

The algo splits the inputs into two pieces of similar size, solves each part and merges the solutions

What does O(n²) imply?

Quadratic time: the algorithm considers pairs of elements

What does O(n^b) imply?

Polynomial time: the algo considers many subsets of the input elements

What does O(1) imply?

constant time

What do \omega(1), \omega(n), \omega(n^b) imply?

superconstant, superlinear, and superpolynomial time (super)

What do o(n), o(c^n) imply?

sublinear, subexponential time (sub)

What does O(c^n) imply?

exponential time

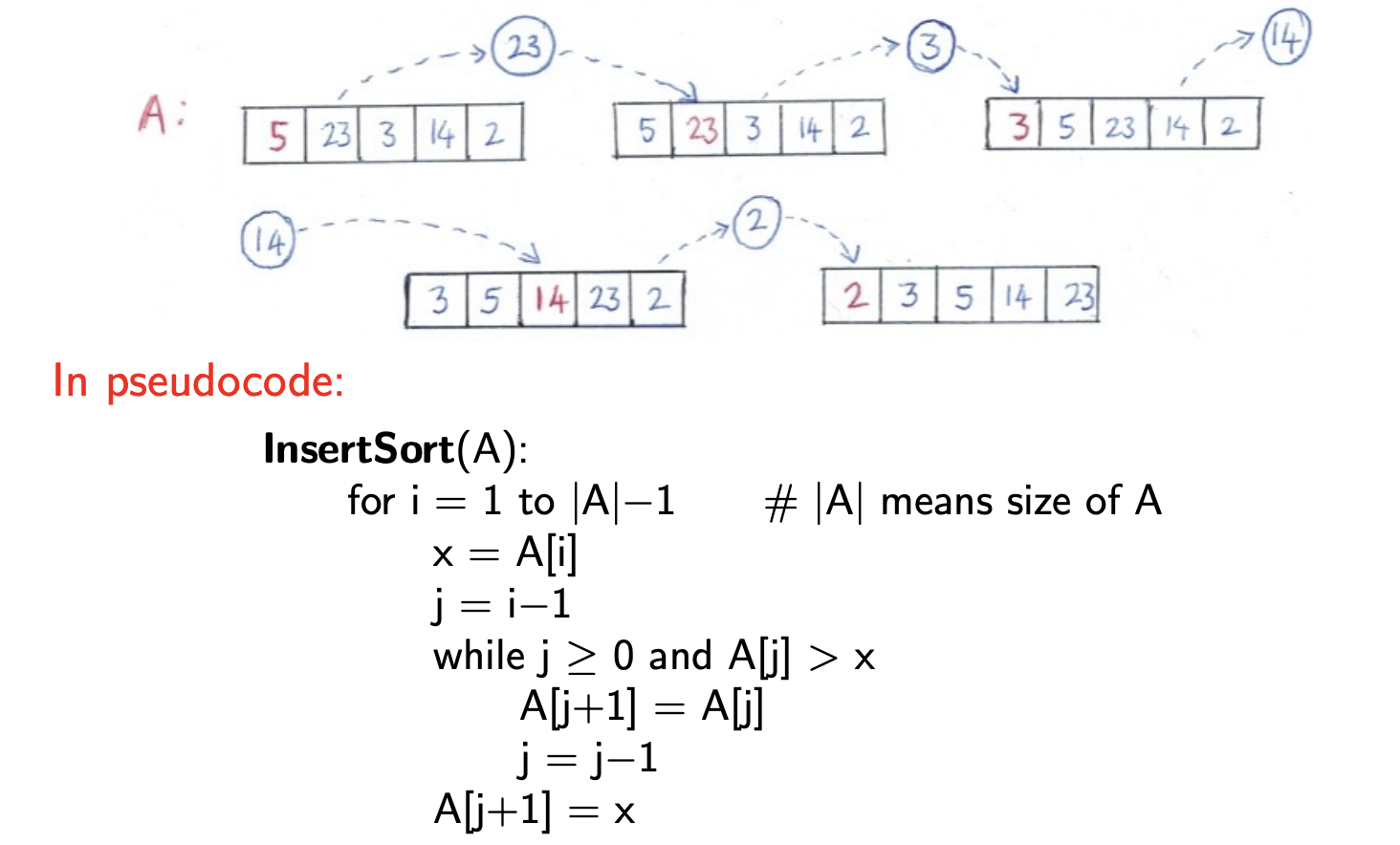
In words, what does the not-in-place InsertSort algo do?

Go through elements of array A STARTING AT INDEX 1, copying them into temporary int B. If any of the elements to the left of currentInt are bigger than currentInt, shift them to the right and place currentInt in the empty space

How much extra space does InsertSort require?

\theta(1)

What is the pseudocode for InsertSort in-place?

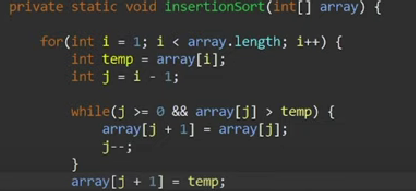
What is the java code for insertionsort?

How much extra space does InsertSort (in-place) require?

Requires \theta(1) extra space

What is the worst-case time complexity of InsertSort in-place?

T_{worst}=T_{av}(n)=\theta(n²)

What is the average-case time complexity of Insert-sort in-place?

T_{worst}=T_{av}(n)=\theta(n²)

What is the best-case time complexity of InsertSort in-place?

T_{best}=\theta (n)

Why is insertionSort preferable to selectionSort?

Best case for insertSort is O(n) or \Theta(n), while selectionSort best case is O(n²)

What is the MergeSort pseudocode?

In words, what does MergeSort do?

Split array A into two halves, sort each separately, then merge the results

What is the worst-case time complexity of MergeSort?

T_{worst}=T_{av}=T_{best}=\theta(nlgn)

What is the average-case time complexity of MergeSort?

T_{worst}=T_{av}=T_{best}=\theta(nlgn)

What is the best-case time complexity of MergeSort?

T_{worst}=T_{av}=T_{best}=\theta(nlgn)

How much extra space does MergeSort require? [2]

Requires \theta(nlgn) extra space, or \theta(n) with a better implementation

what is the pseudocode for recursive merge sort?

which is better, merge sort or insert sort?

MergeSort is asymptotically better than InsertSort, but not in the best case

mergesort = o(insertsort)

For EVERY one choice of a constant k > 0 , you can find a constant a such that the inequality 0 <= f(x) < k*g(x) holds for all x > a

This means that, for large enough inputs, MergeSort will always run faster than Insertion Sort. In other words, MergeSort's performance grows slower than Insertion Sort as the input size increases.

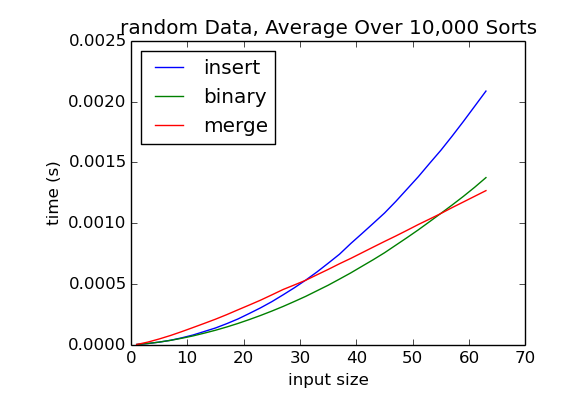
When is insertion sort preferred to merge sort?

In smaller datasets (small n) where memory is a constraint and the array is partially ordered

What does little o mean (where f(n) == o(g))? (equations and words)

\forall c>0;\exists N;\forall n \geq N;f(n) < cg(n)

, equivalently \frac{g(n)}{f(n)} \rightarrow \infty, n \rightarrow \infty

For EVERY one choice of a constant c > 0 , you can find a constant a such that the inequality 0 <= f(n) < k*g(n) holds for all x > a

i.e. g is a strict upper asymptotic bound for f: g grows strictly faster than f as the input size approaches infinity!!

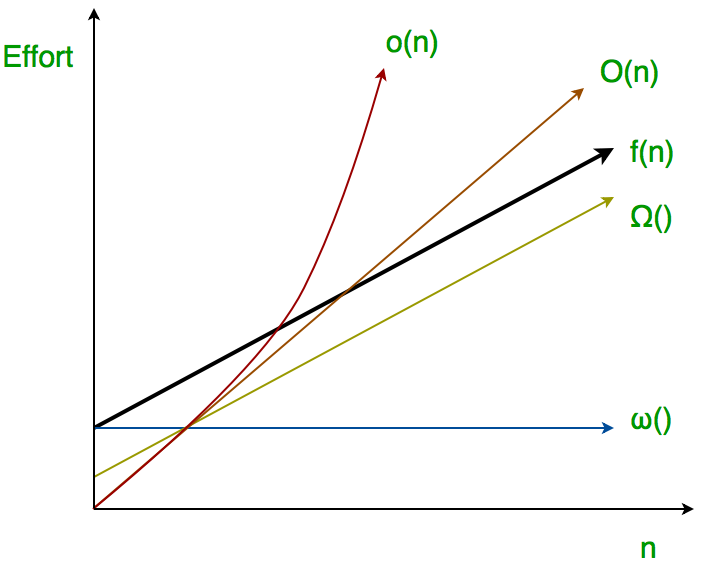
What does big O mean (where f(n) == O(g))? (equations and words)

\exists c>0. \exists N. \forall n \geq N. f(n) \leq cg(n)

For SOME (at least one, there exists) choice of a constant c > 0, you can find a constant a such that the inequality 0 <= f(n) <= c*g(n) holds for all x > a

i.e. g is an upper asymptotic bound (NOT STRICT) for f: g is a limit or ceiling for the growth of f, but f may grow at the same rate or slower than g

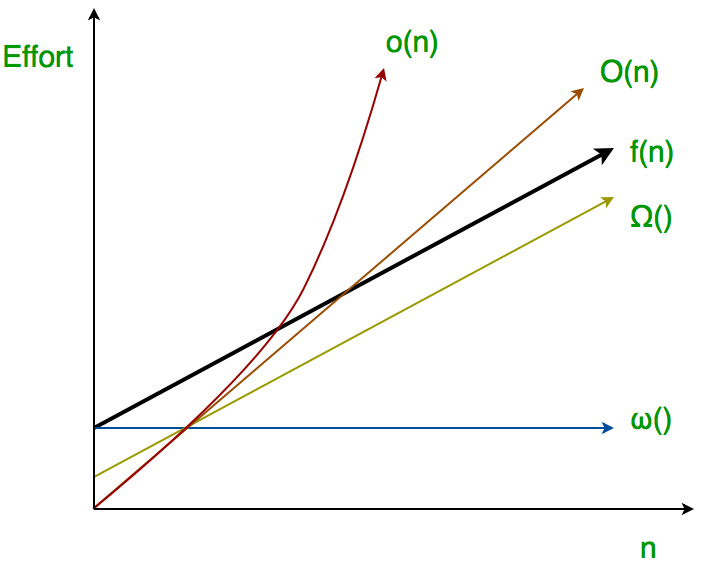
what is the relationship between big O and little o?

f=o(g) \implies f=O(g) , not conversely

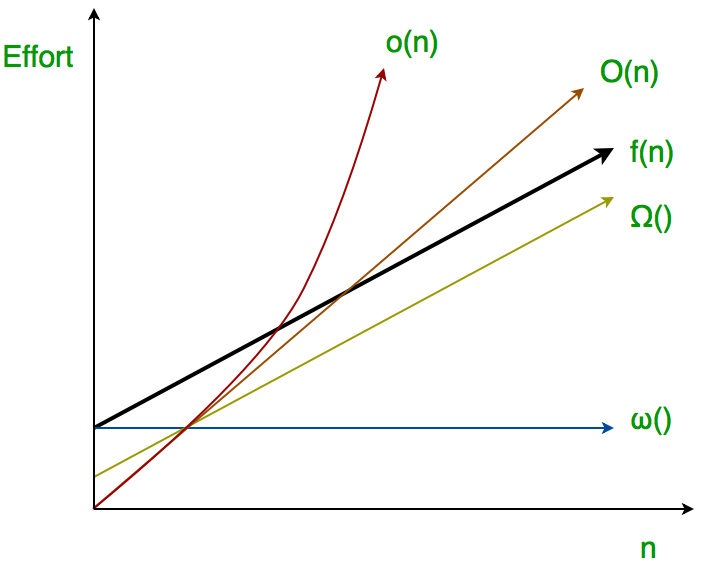
What does \omega mean (where f(n) == \omega(g) )? (equations and words)

\forall c>0. \exists N. \forall n \geq N. f(n) > cg(n)

, f= \omega(g) \iff g=o(f)

For EVERY one choice of a constant c > 0 , there exists a threshold N such that for all n \geq N, the function f(n) grows faster than cg(n).

→ f grows STRICTLY faster than g iff g grows STRICTLY slower than f.

i.e. g is a STRICT asymptotic lower bound of f, so g grows STRICTLY faster than f for sufficiently large n: f(n) == \omega(g)

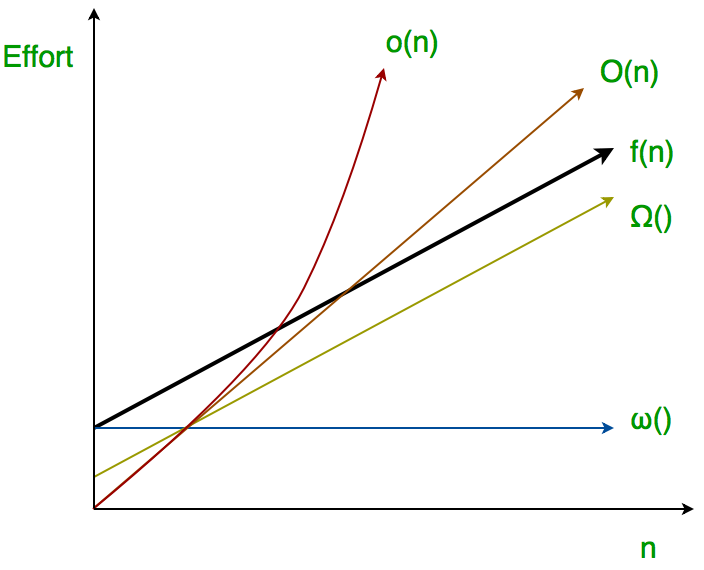
What does \Omega mean (where f(n) == \Omega(g) )? (equations and words)

\exists c>0. \exists N. \forall n \geq N. f(n) \geq cg(n)

, f=\Omega (g) \iff g=O(f)

g is an asymptotic lower bound for 𝑓. This means that 𝑔(𝑛) grows at least as fast as 𝑓(𝑛) for sufficiently large 𝑛.

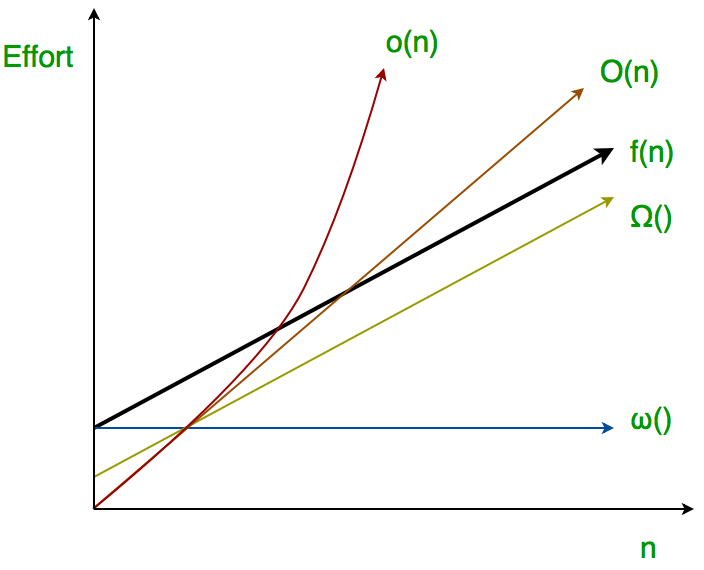
What does \Theta mean (where f(n) == \Theta(g) )? (equations and words)

f = \theta (g) \implies f=O(g) \wedge f=\Omega (g)

\exists c_1,c_2>0. \exists N. \forall n \geq N. c_1g(n) \leq f(n) \leq c_2g(n)

i.e. f(n) is both asymptotically upper and lower bounded by g(n) → g(n) is f’s tight bound, where f grows at the same rate as g(n) for sufficiently large n

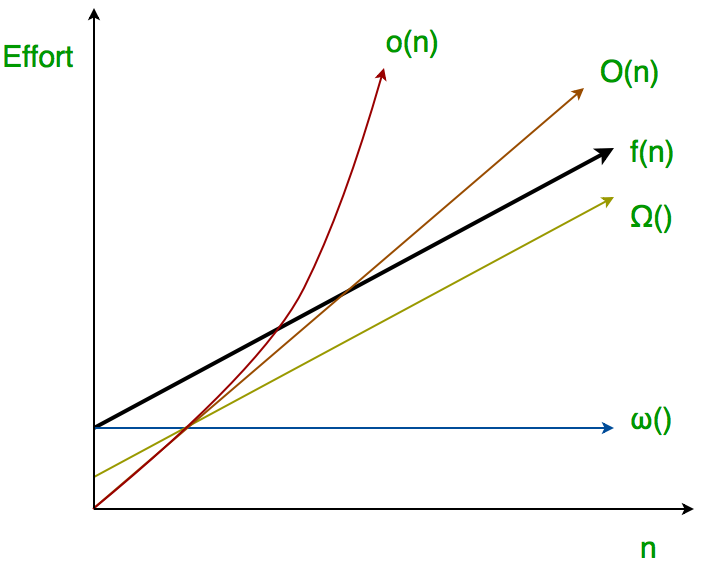
Best/worst case and asymptotic bounds - what does big O and big Omega mean if talking about the worst and best case time complexities?

T_{worst} = O(g) - worst case is no worse than g

T_{worst} = \Omega (g) - worst case can be as bad as g

T_{best} = O(g) - best case can be as good as g

T_{best} = \Omega (g) - best case is no better than g

Time complexity for testing membership (checking if an element exists) in an unsorted array:

O(n)

Since the array is unsorted, you have to iterate through all elements to check if the desired element exists

Time complexity for testing membership (checking if an element exists) in a sorted array

O(log(n))

Binary search can be employed to efficiently locate elements in a sorted array

Time complexity for testing membership (checking if an element exists) in a (singly) linked list [2]

O(1) if you have reference to the node where you want to check

O(n) where you have to traverse from the beginning to the end to check membership

Time complexity for testing membership (checking if an element exists) in an unbalanced tree

O(n)

In the worst case scenario, where the tree is unbalanced and resembles a linked list, testing membership requires traversing all the nodes

Time complexity for testing membership (checking if an element exists) in a balanced tree

O(log(n))

Due to the balanced nature of the tree, operations like searching can be performed efficiently using techniques like binary search

Time complexity for adding or removing elements in an unsorted array:

O(n)

Adding or removing an element may require shifting elements to maintain order; you have to iterate through all elements to check if the desired element exists

Time complexity for adding or removing elements in a sorted array:

O(log(n))

Binary search can also be used to find the correct position for insertion or deletion, but shifting elements may still be necessary

Time complexity for adding or removing elements in a linked list:

O(1) - if adding or removing an element at the beginning of the linked list since it only involves adjusting a few pointers

O(n) - for positions NOT at the beginning of the linked list, you may need to traverse the list to find the insertion or deletion point

Time complexity for adding or removing elements in an unbalanced tree:

O(n)

If the tree is unbalanced, adding or removing elements may require traversing through most or all nodes to maintain balance

Time complexity for adding or removing elements in a balanced tree:

O(log(n))

Since balanced trees maintain their balance through rotations or other techniques, adding or removing elements can be done efficiently

Is a stack LIFO or FIFO?

LIFO

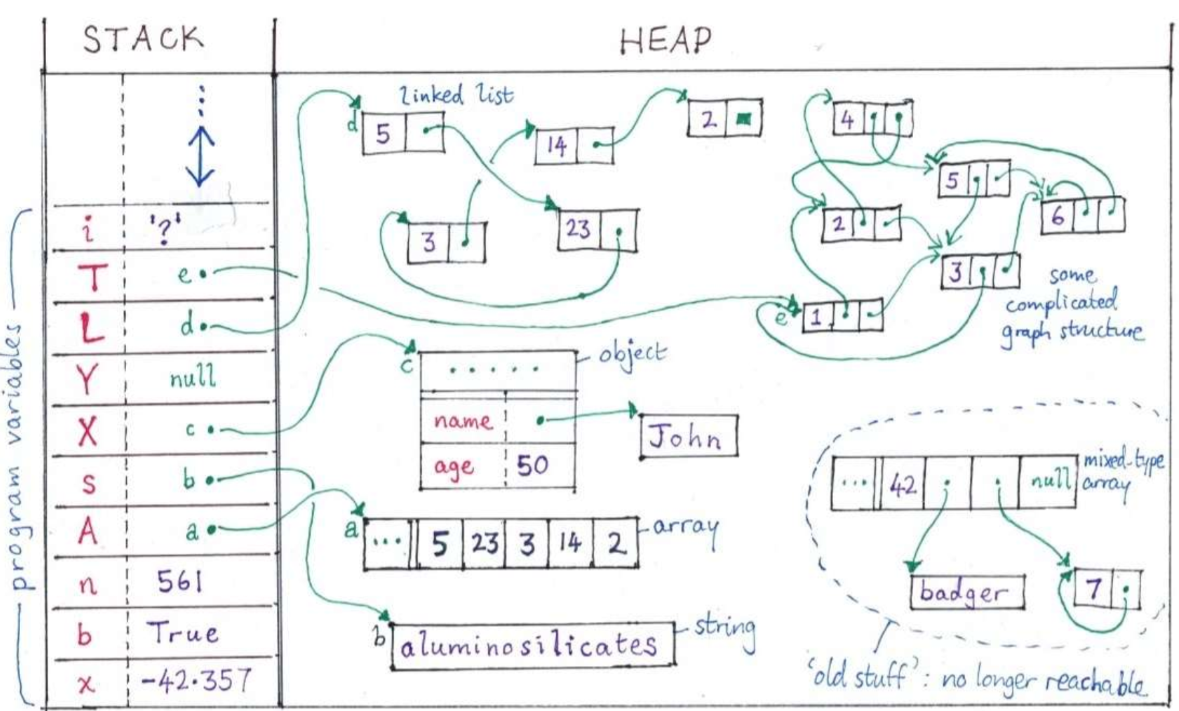
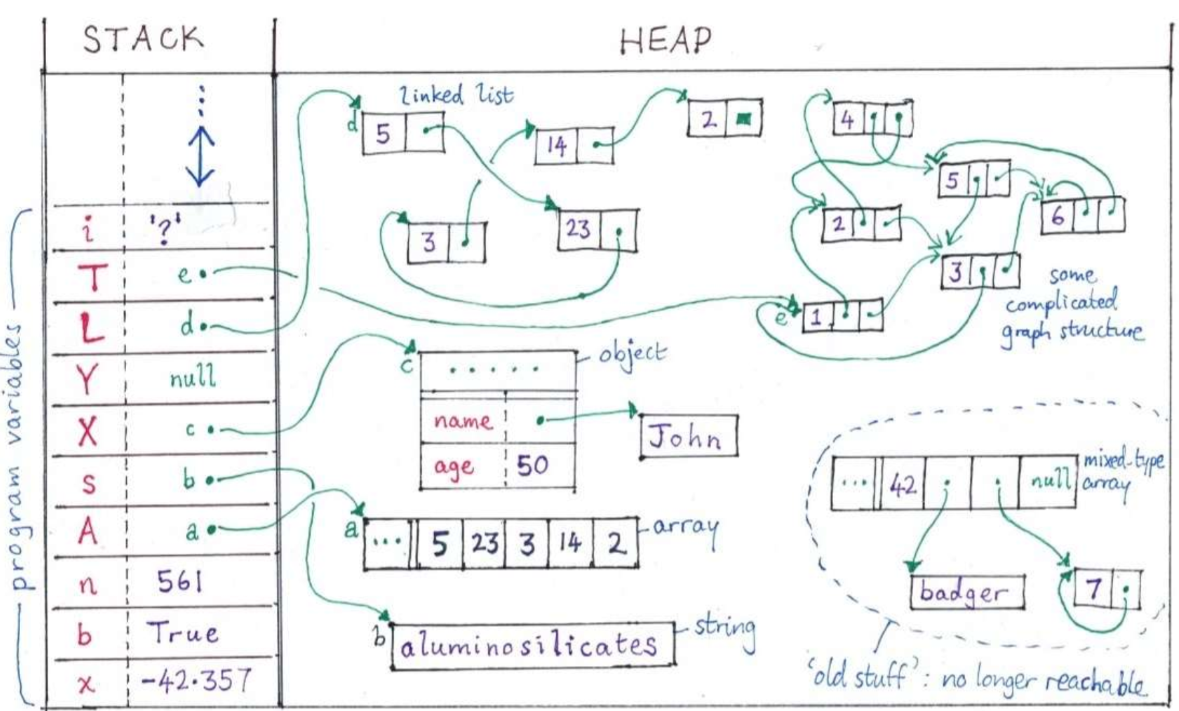
What does the stack store, and what’s a special characteristic of what the stack stores? [4]

Program variables:

• local variables

• function parameters

• references to elements on the heap

All program variables are items which must have fixed size

Is a stack dynamic or static?

Dynamic - it grows and shrinks as variables enter and exit scope

What are local variables?

Variables declared within a function or block of code, which are created and stored on the stack when the function is called.

How are local variables and function parameters (stack-based variables) removed from the stack?

Since stack-based variables are scoped to the function or block in which they are declared, they have a limited lifetime. When the function exits or the block of code ends, the memory allocated to these variables is deallocated, and they cease to exist.

How are function parameters stored on and removed from the stack?

When a function is called, its parameters are passed to the function and stored on the stack. These parameters can be accessed

Where do heap objects live once created (allocated)?

Anywhere in memory

What happens in many languages when heap objects become unreachable?

languages inc. Java, Python, Haskell

a garbage collector (memory recycler) detects this and reclaims the space

What are some specifications of heap objects?

They can be of any size and may contain reference to other heap objects

What are the three methods for modular exponentiation? (pseudocode)

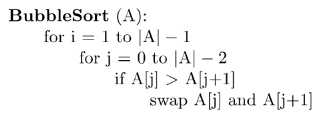
Given this relatively inefficient bubble sort algo pseudocode, what is a more efficient version?

What are the 4 common functions and return types of finite sets of items of a given type X?

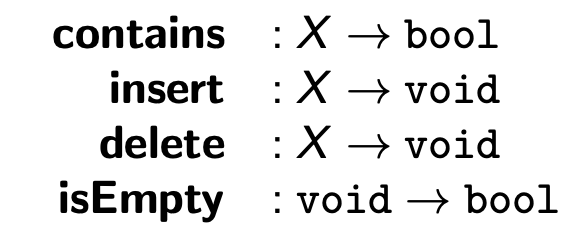
What are the functions and return types of dictionaries (mapping keys of type X to values of type Y)?

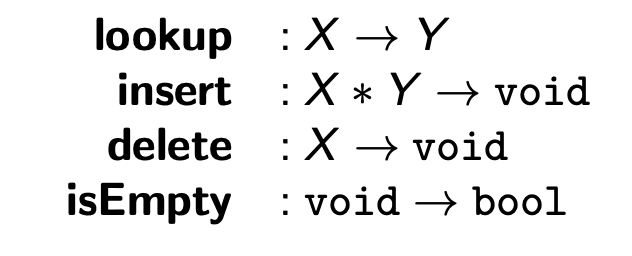
What is the pseudocode for BinarySearch(A,key,i,j)?

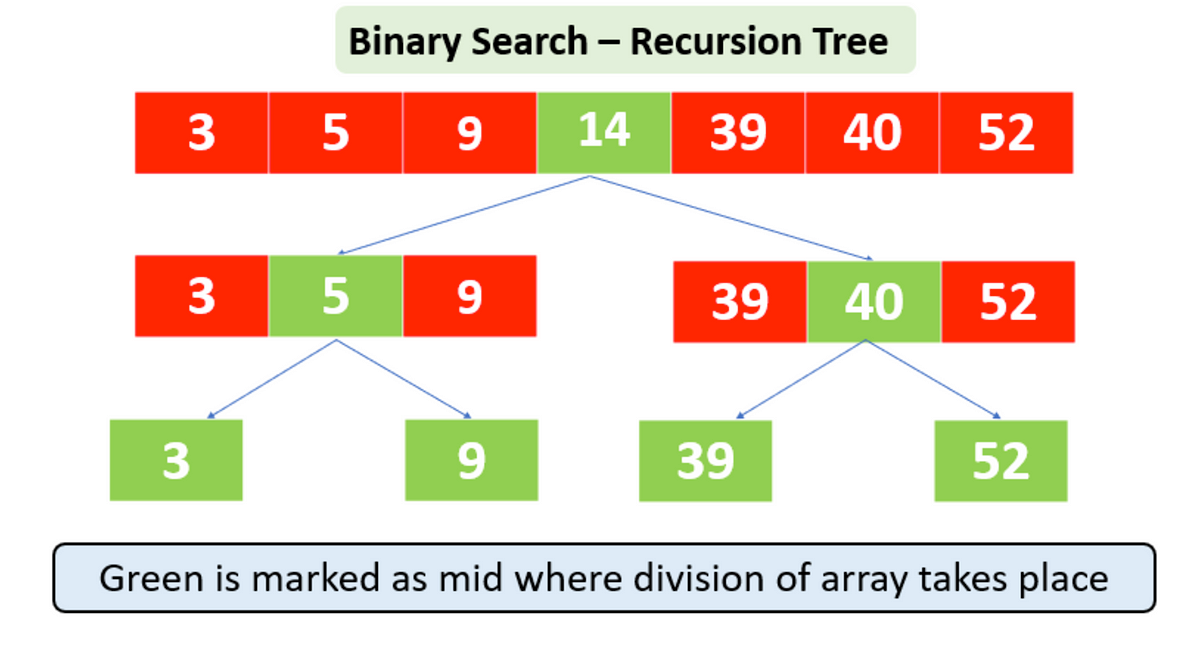
Explain binary search in English (plus diagram)

Binary search is an efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing in half the portion of the list that could contain the item, until you've narrowed down the possible locations to just one.

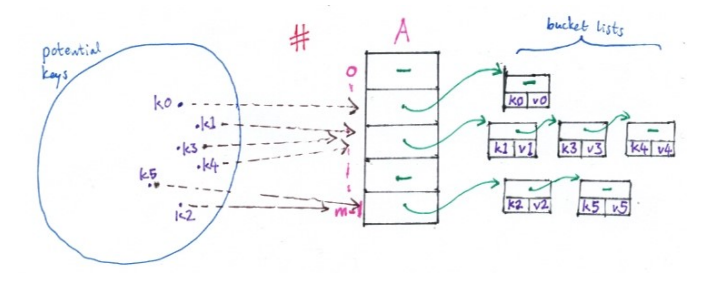
What is the point of a hash (#) table?

Where there are K potential keys (huge) compared to n actual keys ‘currently in use’ (much smaller)

What is the hashing method?

use a chosen hash function # mapping an array of potential keys s to integers 0, …, m-1 (hash codes), where m \approx n, such that #(s) = (x(s) mod m); then try to use an array A of size m, storing the entry for key s at position #(s) in A

What is a clash?

a collision when trying to map keys s to hashcodes 0, …, m-1 (when trying to hash a set)

What are the two methods to resolve hash clashes?

1) bucket list hash tables

2) open addressing and probing

What is a bucket-list hash table?

A hash table where we store a list (“bucket”) of entries for each hash value, external to the hash table

What is the load, \alpha on the hash table?

the ratio \alpha = \frac{n}{m}, which may be \leq1 or >1 (i.e. cannot be 1), where n = number of elements in the hash table and m = size of hash table (number of slots or linked lists/buckets in the table)

What is amortised time?

the way to express the time complexity when an algorithm has the very bad time complexity only once in a while besides the time complexity that happens most of time. Good example would be an ArrayList which is a data structure that contains an array and can be extended.

When do we “expand-and-rehash”?

When we have chosen a desired load factor \alpha and our load factor exceeds this, we can increase the size of the hash table and rehash all the elements into the new, larger hash table

Why do we desire a low load factor \alpha?

It ensure that the hash table remains efficient by minimising the likelihood of collisions

What is the time complexity for an unsuccessful lookup, assuming that for k not in the table, #(k) is equally likely to be any of the m hash codes in the hash table?

If computing #(k) takes O(1) time, the average time for unsuccessful lookup is \theta(\alpha) (where a\rightarrow infinity, and thus = \theta(n)

Assuming that all k keys in a hash table are equally likely to be searched for, what is the average time for a successful lookup operation?

Time complexity in the order of \theta(\alpha) , where a is the load factor

What is open addressing?

Storing all items within the hash table itself, rather than keeping bucket lists outside the hash table (as in bucket-list hash tabling)

How do we deal with clashes in open addressing?

Don’t use a simple hash function #(k), but a function #(k, i) where 0 \leq i<m

What would be the first few choices if hashing to key k in open addressing?

• 1st choice: #(k, 0)

• 2nd choice: #(k, 1)

• etc.

How do we insert an item e with key k into an open-addressed hash table?

probe A[#(k, 0)], A[#(k, 1)], . . . until we find a free slot A[#(k, i)], then put e there

How do we lookup an item with key k in an open-addressed hash table?

To lookup an item with key k, probe A[#(k, 0)], A[#(k, 1)], . . . until we find either an item with key k, or free cell (lookup failed).

What is the worst-case time complexity for functions lookup/insert/delete when using hash tables?

\theta(n)

If we could avoid clashes entirely, what would worst-case lookup be in hash tables?

\theta(1)

What does it mean in hashing when keys are “static”?

no insert or delete functions required

What is only worth doing in the case of static keys when hashing?

finding a perfect hash function (with NO clashes) for this set of keys

What are the pros of probing? [2]

• Functions insert and lookup expect a low number of probes until the hash table is nearly full

  • n_{probes} \approx \frac{1}{1-a} if unsuccessful lookup

  • less for successful lookup

• No need for pointers

  • Saves memory which can be ‘spent’ on increasing table size and decreasing load \alpha, leading to faster lookup for same memory

What are the cons of probing? [2]

• delete operation can be less efficient than other data structures!! Involves either:

  • leaving tombstone markers

  • rehashing the table

• design of probing functions requires careful consideration (to optimise hash table performance)

  • trade-offs with efficiency, collision resolution, complexity

What are some different types of probing?

linear probing, quadratic probing, double hashing

Binary tree (representation of sets) - what are the properties of the nodes?

Each node x has a left and right branch, each of which may be null or a pointer to a child node.

AND the values of its left descendent node < current node < right descendent node

What is the time complexity of the contains function in a tree, balanced/unbalanced?

Contains takes O(log(n)) for balanced/unbalanced, however worst case is O(n)

What is the time complexity of the insert function in a tree, balanced/unbalanced?

Insert takes O(log(n)) if the tree is not too unbalanced, \theta(n) in worst case

What is the depth of a perfectly balanced tree?

d =\left \lfloor{log(n)}\right \rfloor

What is a red-black tree?

A self-balancing binary search tree in which every node is coloured with either red or black. They are guaranteed to be “not too unbalanced”.

What is the time complexity of all operations in red-black trees? What about the complexity of re-balancing trees?

O(log(n)) for insert, delete, rebalance

What are the properties of a red-black tree?

• Root and all (trivial) leaves are black (trivial leaves are the tiny dots/triangles at the end of the branches)

• All paths root to leaf (nil descendants) contain same number of black nodes (b, black-length)

• On a path root to leaf, never have two reds in a row

• min path length is b, max is 2b-1, so path lengths are under 2(log(n+1))+1

• If a node is red, then its kids are black

• Smaller elements will always be to the left, and bigger to the right, of nodes

What is the red-uncle rule?

When inserting a node we colour it red. If the node’s parent and uncle are red, colour them black, and the grandparents red. This pushes reds UP. We apply red-uncle rule until the endgame scenario.

If uncle is red, recolour parent, grandparent and uncle.

How many times should we repeat the red-uncle rule?

Until we reach an endgame scenario

What are the endgame scenarios of red-uncle rule when inserting a node?

1: tree is legal, do nothing

Do something:

2: the root is red

3: newNode.uncle.colour == black (TRIANGLE)

4: newNode.uncle.colour == black (LINE)

What are the fix-up steps if after insertion of a node in the r-b tree, the root is red?

Colour it black (adds 1 to all black lengths)

What are the fix-up steps if the newly inserted node’s uncle is red?

Recolour parent, gp, and uncle

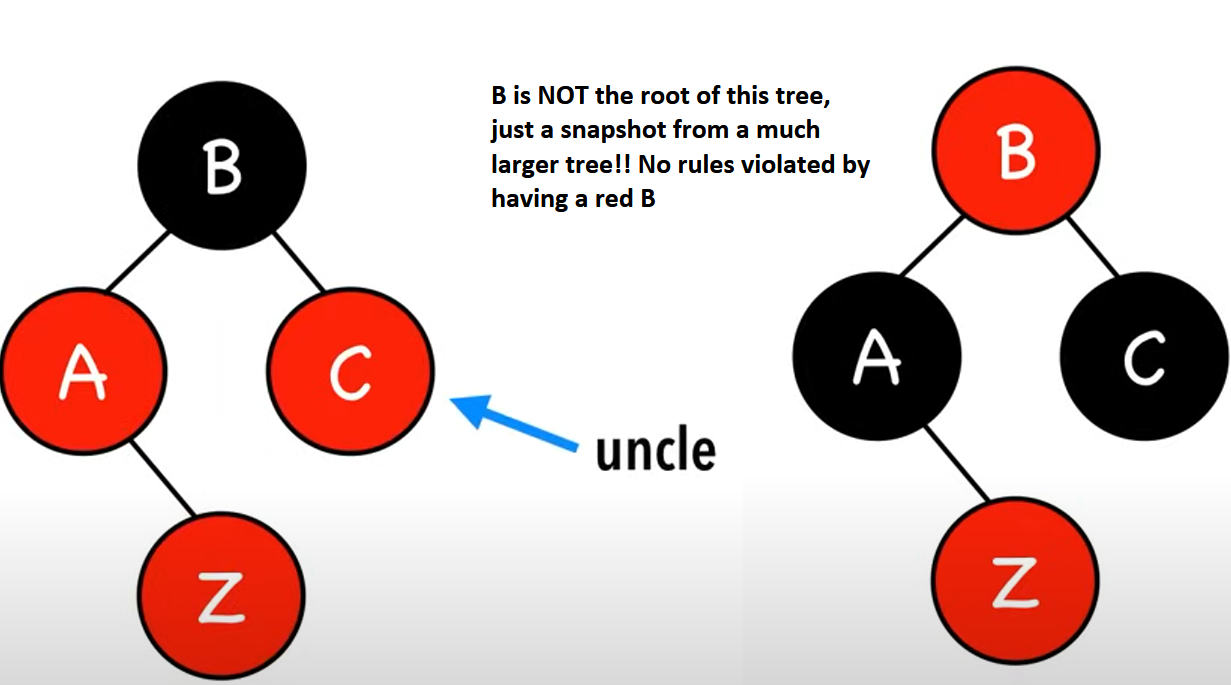
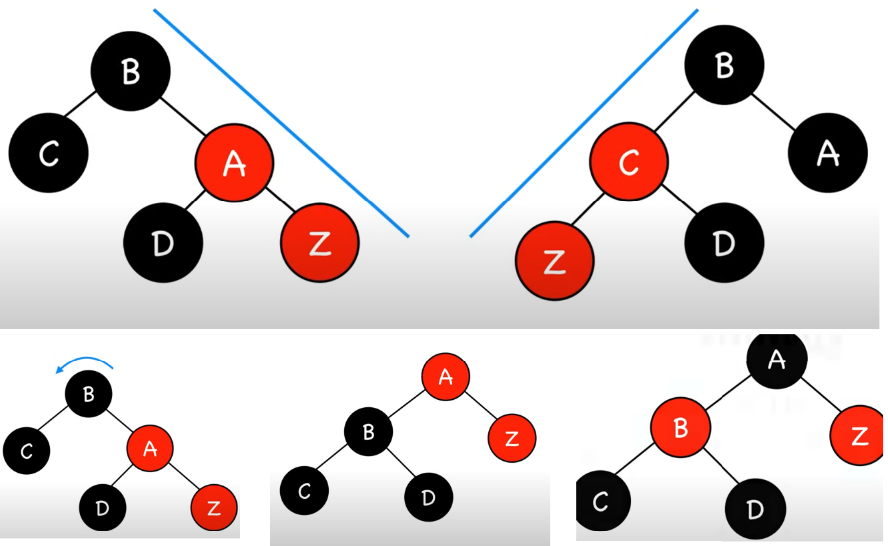
What are the fix-up steps if the newly inserted node’s uncle is black (and there’s a triangle between Z, Z’s parent and Z’s grandparent)?

Rotate Z’s parent in the direction of the triangle

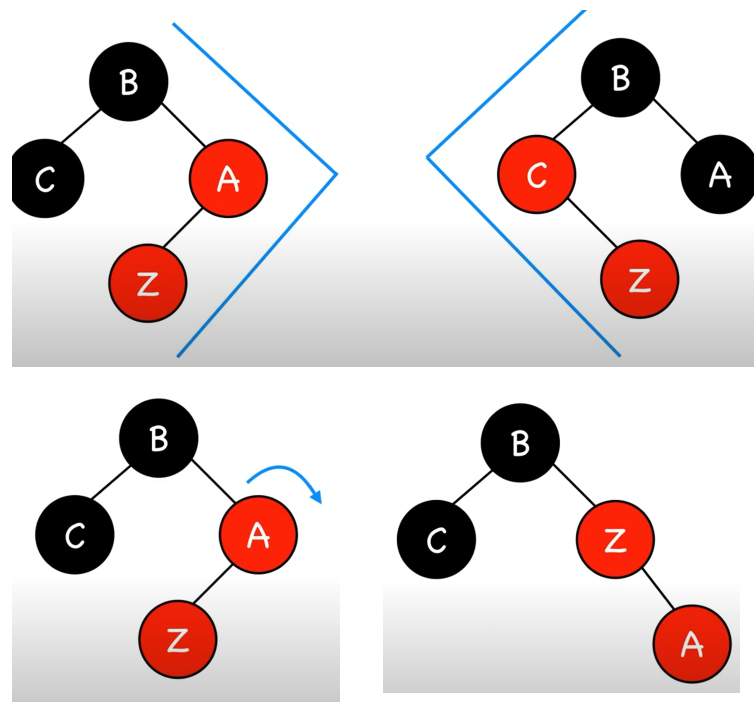
What are the fix-up steps if the newly inserted node’s uncle is black (and there’s a straight line between Z, Z’s parent and Z’s grandparent)?

Rotate grandparent (in the up and over direction) and recolour gp