Topic A flaschards

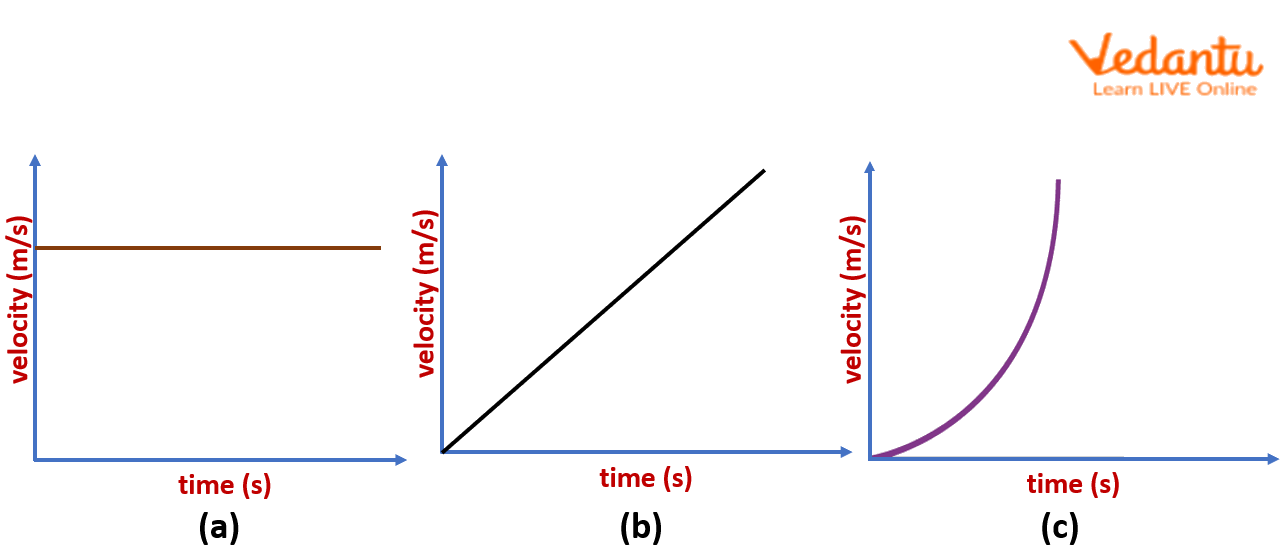
velocity time graph

(A.1 Kinematics)

gradient= acceleration

y-intercept= initial velocity

area=displacement.

• Straight (diagonal) line represents uniform acceleration

• A curved line represents non-uniform acceleration

• A Horizontal line represents motion with constant velocity

displacement time graph

(A.1 Kinematics)

Slope= velocity

y-intercept=initial displacement

A straight (diagonal) line represents a constant velocity

A curved line represents an acceleration

A Horizontal line represents a state of rest

The area under the curve is meaningless

acceleration time graph

(A.1 Kinematics)

Slope is meaningless

y-intercept= initial acceleration

Area = change in velocity

A straight line indicates uniform acceleration

A zero slope (horizontal line) represents an object undergoing constant acceleration

How do you find instantaneous speed and velocity of an object?

(A.1 Kinematics)

To find the instantaneous velocity on a displacement-time graph:

- Draw a tangent at the required time

- Calculate the gradient of that tangent

Projectile motion

(A.1 Kinematics)

- Divide SUVAT into two components: Horizontal and vertical

- The acceleration due to gravity is constant and downward throughout the motion

- The horizontal velocity, is constant and a=0 (if no fluid resistance).

- The vertical velocity, changes in magnitude and direction throughout the motion

Time of flight (projectile motion)

(A.1 Kinematics)

u=usin0, v= 0, a=-9.81, t=?

Maximum height attained

(A.1 Kinematics)

u=usin0, v= 0, a=-9.81,s= ?

Range (projectile motion)

(A.1 Kinematics)

u=ucos0, t=(2usin0)/g, a =0, s= ?

Terminal velocity

(A.1 Kinematics)

acceleration=zero

constant velocity

Forces are balanced: F_resistive=F_mg

Displacement=

(A.1 Kinematics)

velocity x time

Motion of a bouncing ball

(A.1 Kinematics)

- acceleration is constant

- between highest and lowest points velocity changes instantaneously from negative to positive

- max points: max displacement

-min points: min displacement

Factors that decrease in fluid resistance in projectile motion

(A.1 Kinematics)

- Time of flight

- Horizontal velocity

- Range

- Max height

Newton's 1st law

(A.2: Forces and Momentum)

A body will remain at rest or move with constant velocity unless acted on by a resultant force

Newtons 2nd Law

(A.2: Forces and Momentum)

F=ma

The resultant force on an object is directly proportional to its acceleration

Newtons 3rd law

(A.2: Forces and Momentum)

Every action has an equal and opposite reaction

A Newton's third law force pair must be:

- Same type of force

- Same magnitude

- Opposite in direction

- On different objects

Hooke's Law

(A.2: Forces and Momentum)

The extension of the material is directly proportional to the applied force.

Conservation of linear momentum

(A.2: Forces and Momentum)

The total linear momentum before a collision equals the total linear momentum after a collision unless a resultant external force acts on the system.

Elastic collisions

(A.2: Forces and Momentum)

- kinetic energy is conserved

- Objects colliding do not stick together and move in opposite directions after collision

Inelastic collisions

(A.2: Forces and Momentum)

- Kinetic energy is not conserved

- Objects colliding stick together and move in together after collision

Two-dimensional collisions and explosions

(A.2: Forces and Momentum)

Done by resolving vectors: splitting into horizontal and vertical components.

- X direction: cos0

- y Direction: sin0

Uniform circular motion (vertical circle)

(A.2: Forces and Momentum)

Centripetal force + gravitational force

- Maximum force at bottom

- Minimum force at top

conservation of momentum along the x direction

(A.2: Forces and Momentum)

mu + 0 = m1v1cos01 + m2v2cos01

conservation of momentum along the y direction

(A.2: Forces and Momentum)

0+0 = m1v1sin01 - m2v2sin02

Forces on object down a slope

(A.2 Forces and momentum)

Gravitational force: F_g= mg

• Parallel to slope: F_g= mgsin(θ)

• Perpendicular (Normal force): F= mgcos(θ)

Acceleration of object down the slope: a=gsin(θ) (assuming no friction)

Frictional force: F_f= μ x mgcos(θ)

• F_net= mgsin(θ) - μ x mgcos(θ)

• a=g(sin(θ)−μcos(θ))

Forces on object up a slope

(A.2 Forces and momentum)

Gravitational force: F_g= mg

• Parallel to slope: F_g= mgsin(θ)

• Perpendicular (Normal force): F= mgcos(θ)

Frictional force: Ff= μ x mgcos(θ)

Fnet= F_applied - F_{g parallel} + F_friction

How do you see if forces are in equilibrium?

• F_net=0

• Must form a closed triangle

• From tip to tail

Force x displacement graph

(A.3: Work, Energy, Power)

Area= work done

Principle of conservation of energy

(A.3: Work, Energy, Power)

Energy is not created or destroyed, it only changes form.

Total energy of a closed system always stays the same

mechanical energy

(A.3: Work, Energy, Power)

sum of kinetic energy, gravitational potential energy and elastic potential energy

Under what circumstances will the mechanical energy of a system be conserved?

(A.3: Work, Energy, Power)

No frictional forces

Distance vs. Displacement

(A.1 Kinematics)

Distance: total path traveled (scalar).

Displacement: straight-line change in position (vector).

average velocity

(A.1 Kinematics)

total displacement divided by the total time taken

Forces

(A.2: Forces and Momentum)

interactions between bodies that can cause acceleration

Free body diagrams

(A.2: Forces and Momentum)

a diagram showing all the forces acting on an object

You can analyze the resultant (net) force by summing vectors to apply Newton's second law.

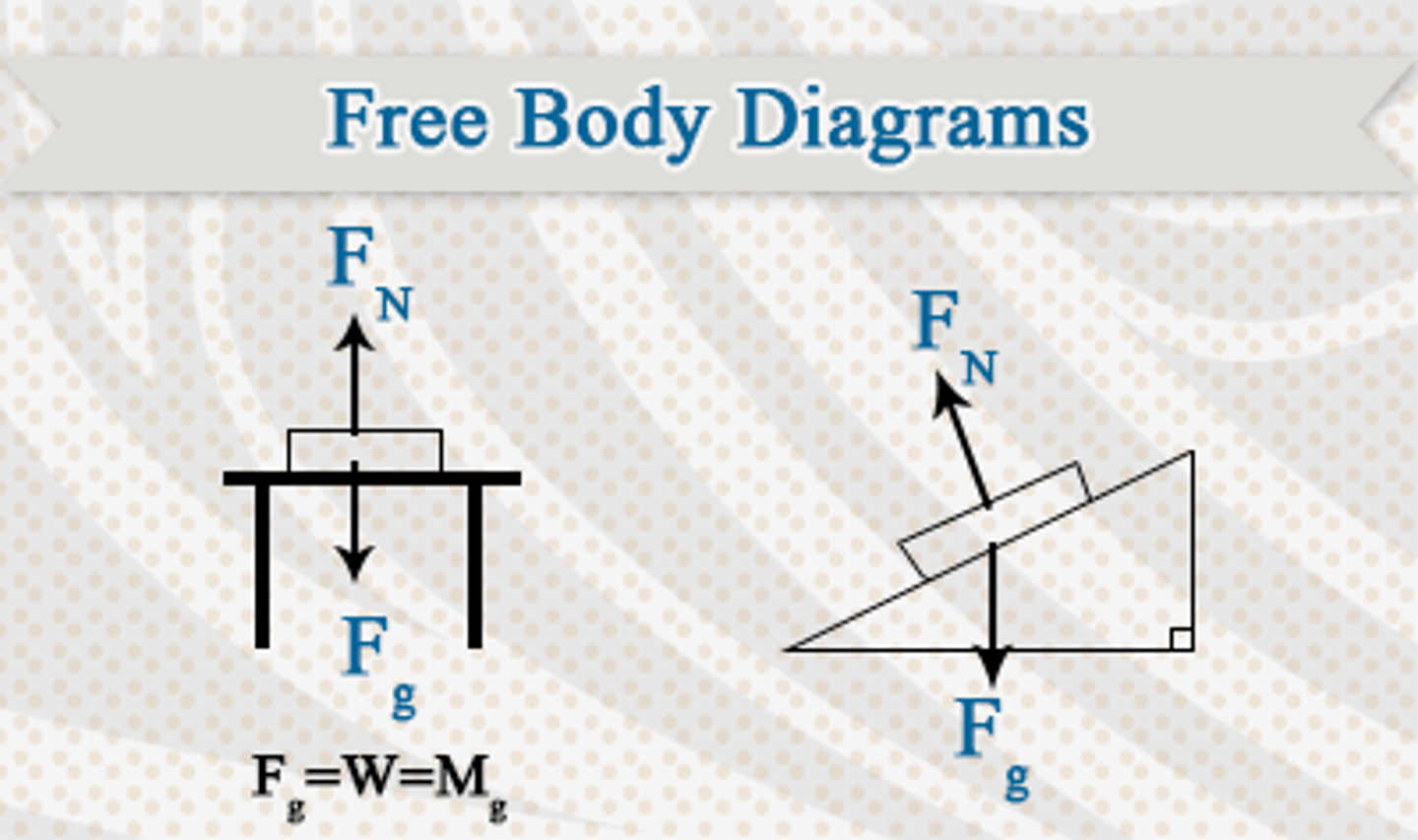
Normal force

(A.2: Forces and Momentum)

• Force exerted by a surface or contact point

• Acts perpendicular to surface

• Prevents objects from falling into surface

Rest: N=mg

Pushing down= N=mg + F_down

frictional force

(A.2: Forces and Momentum)

acts parallel to the surface and opposes motion or attempted motion between surfaces.

Opposes motion in any direction: right, left, up, or down

if there is an angle involved, it is equal to:

F=W x sin (0).

What's the difference between static and dynamic friction?

(A.2: Forces and Momentum)

Static friction prevents motion up to a maximum limit, while dynamic friction acts when the object is already moving.

Impulse

(A.2: Forces and Momentum)

change in momentum resulting from a force acting over a time interval.

What happens in an explosion in terms of momentum?

(A.2: Forces and Momentum)

The total momentum before explosion is zero, so after the explosion, fragments move in opposite directions to conserve momentum.

What causes circular motion?

(A.2: Forces and Momentum)

A centripetal force that acts towards the center of the circle.

Work

(A.3: Work, Energy, Power)

transfer of energy due to a force acting over a displacement.

What does it mean if mechanical energy is conserved?

(A.3: Work, Energy, Power)

No energy is lost to heat or other forms, so energy is just changing between kinetic, potential, or elastic.

Power

(A.3: Work, Energy, Power)

The rate of work done (or the rate at which energy is transferred).

Sankey diagram

(A.3: Work, Energy, Power)

A scale diagram used to represent the total input, the useful output and the wasted output energies within a system.

Rigid body assumption

(A.4: Rotational Motion)

- An object that doesn't deform under force

- All points in the body maintain fixed positions to each other

- Rotational and translational motion can be analyzed separately

Moment of inertia

(A.4: Rotational Motion)

How difficult it is to make a body accelerate

measure of an object's resistance to changes in its rotational motion

• The farther the mass is from the axis, the larger the moment of inertia

• The larger, the harder as there is less acceleration

• Hollow objects: greater moment of inertia

Torque

(A.4: Rotational Motion)

a force that causes rotation

measure of how much a force acting on an object causes that object to rotate

Angular momentum

(A.4: Rotational Motion)

rotational momentum of a spinning or orbiting object

principle of conservation of angular momentum

(A.4: Rotational Motion)

The angular momentum of a system remains constant if no external torques act on it.

In rotational motion, gravitational potential energy gets transferred into...

(A.4: Rotational Motion)

Linear Ek, and Rotational Ek.

Torque against time graph

(A.4: Rotational Motion)

Area= Angular impulse

Density

Another word for material

What does it mean when a system is in equilibrium?

(A.4 Rotational motion)

• τ_clockwise=τ_{counter-clockwise}

• ∑τ=0

Newton's second law for rotation

(A.4: Rotational Motion)

the sum of all torques acting on a rotating object is equal to the product of the object's moment of inertia and its angular acceleration

What causes a change in angular momentum?

(A.4: Rotational Motion)

A resultant torque over time, called angular impulse

• If torque depends on the angle of the force, no constant angular acceleration, can't use analogous SUVAT equations

• τ=F⋅r⋅sin(θ)

When is angular momentum conserved?

(A.4: Rotational Motion)

When there is no external torque acting on the body.

What is an inertial reference frame?

(A.5: Relativity)

A non-accelerating frame where Newton's laws hold true.

What are the two postulates of special relativity?

(A.5: Relativity)

- The laws of physics are the same in all inertial frames.

- The speed of light in a vacuum is constant in all inertial reference frames.

Lorentz factor

(A.5: Relativity)

A way of transforming and expressing velocities in speed of light

Proper time (t0)

(A.5: Relativity)

Time measured by an observer at rest relative to the event.

How do you move forward in time relative to someone on Earth?

(A.5: Relativity)

Moving super fast relative to them for a long time.

proper length (Lo)

(A.5: Relativity)

Length measured in the rest frame of the object.

When does the length of objects appear to shrink relative to someone?

(A.5: Relativity)

The length of very fast moving objects

What does the relativity of simultaneity mean?

(A.5: Relativity)

Events that are simultaneous in one frame may not be simultaneous in another.

What do space-time diagrams show?

(A.5: Relativity)

The motion of particles over time, with time labeled as ct and distance as t.

What does the angle θ on a space-time diagram represent?

(A.5: Relativity)

The particle's speed

Multiple frames of reference in space-time diagrams

(A.5: Relativity)

S: Read directly from axes

S': Draw lines parallel to ct' and x' axes

What experiment supports time dilation and length contraction?

(A.5: Relativity)

Muon decay experiments—muons reach Earth's surface because time dilates in their frame.

Space time intervals

(A.5: Relativity)

- Invariant: They are the same from one reference frame to another

- Used to measure ho far apart two event are in spacetime

Invariant quantities

(A.5: Relativity)

- Proper time interval (t0)

- Proper length (L0)

- Space time interval (s)