Precalc MUST KNOW

Secant Line

A line formed between 2 points, a and b, using the Average Rate of Change formula.

formula for Average ROC on an interval [a,b] (a,f(a)), (b,f(b)), slope of secant line

f(b) - f(a) / b - a

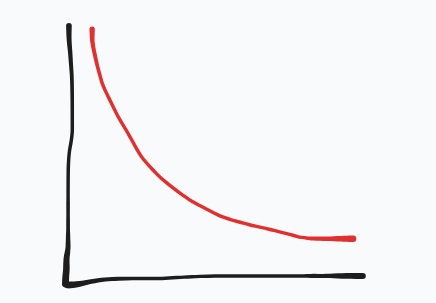
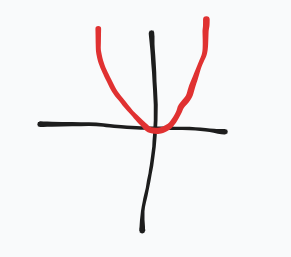
Evaluate this graph

f(x) decreases, and ROC is increasing, curve is concave UP

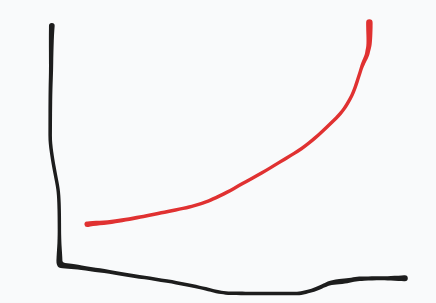
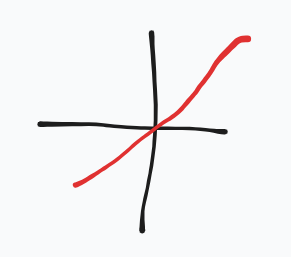
evaluate this graph

f(x) increases, ROC increases, the curve is concave UP

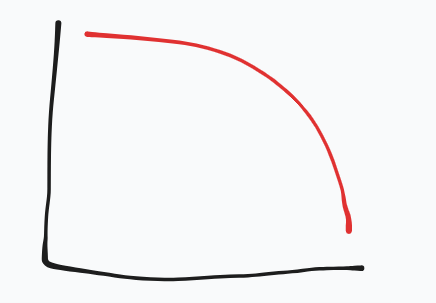
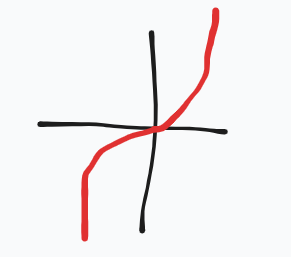
evaluate this graph

f(x) decreases and ROC is decreasing, curve is concave DOWN

Increasing

Positive ROC

Decreasing

Negative ROC

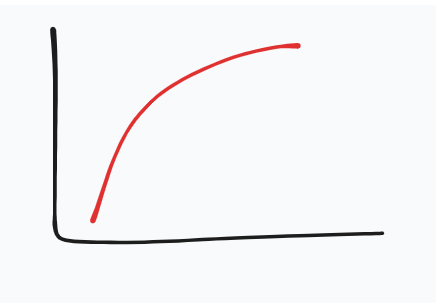
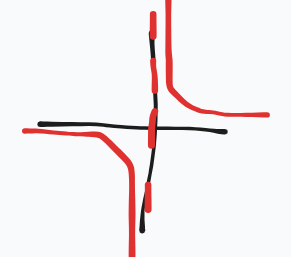
evaluate this graph

f(x) increases ROC decrease curve is concave DOWN

Concave up

ROC is increasing

Concave down

ROC is decreasing

An odd function…

a function where f(-x) = -f(x) for all x in the domain. (passes through the orgin and is symmetric over the origin.)

An even function is…

a function wheref(-x) = f(x) for all x in the domain. (symmetric over the y-axis.)

(x-a)¹

is a linear factor representing a zero of the polynomial at x = a. (crosses through the x-axis at this point)

(x-a)²

is a repeated factor representing a zero of the polynomial at x = a with a multiplicity of 2. (touches the x-axis at this point but does not cross it)

(x-a)³

is a repeated factor representing a zero of the polynomial at x = a with a multiplicity of 3. (crosses the x-axis with a change in direction at this point)

to find x-intercepts…

set y, or f(x) equal to zero and solve for x.

to find y-intercepts…

set x equal to zero and solve for y.

Complex Conjugate

a pair of complex numbers of the form a + bi and a - bi, where i is the imaginary unit. aka, imaginary zeros must come in pairs

Limit notation is expressed as…

lim (x -> a) f(x) = L (where L is the limit as x approaches a)

End behaivor of an odd degree…

polynomial has opposite signs at each end. As x approaches positive infinity, f(x) approaches positive or negative infinity, and as x approaches negative infinity, it approaches the opposite.

End behaivor of an even degree…

polynomial has the same sign at both ends. As x approaches positive or negative infinity, f(x) approaches positive or negative infinity on both ends.

Leading coefficient is positive… (end behavior)

up on the right

Leading coefficient is negative… (end behavior)

down on the right

A values 2 functions in transformations of polynomials

• Vertical reflection across x-axis for a<0

• Vertical stretch or compression.

B values function in transformations of polynomials

horizontal dilation by factor of 1/b

H values function in transformation of polynomials

horizontal translation in the direction of -h

K values function in transformation of polynomials

vertical translation in the direction of k

Linear function in a table…

if both input and output values change consistantly

Quadratic function in a table…

if input values change consistently and 2nd difference output values are equal

Cubic function in a table…

if input values change consistently and 3rd difference output values are equal.

Exponential function in a table…

if input values change consistently and output values change proportionally

Logarithmic functions in a table…

if input values change proportionally, and output values change consistently.

General form of rational functions

is written as f(x) = A(x)/B(x), where A and B are polynomials and B(x) ≠ 0.

How a vertical asymptote is formed in a rational function…

occurs when the denominator B(x) is zero while the numerator A(x) remains non-zero, leading to undefined values.

How a horizontal asymptote is formed in a rational function…

is determined by the degrees of the polynomials A(x) and B(x). If the degree of A is less than that of B, y=0 is the horizontal asymptote; if they are equal, the asymptote is y = leading coefficient of A / leading coefficient of B. And if the degree of A is greater, there is no horizontal asymptote but a slant asymptote. (remember BOBO BOTN EATS DC)

How a slant/oblique asymptote is formed and found in a rational function…

occurs when the degree of the numerator A(x) is exactly one greater than the degree of the denominator B(x). It is found by performing polynomial long division, giving a linear function as the asymptote.

Pascals triangle and binomial expansion

is a triangular array of the binomial coefficients. It is used to expand expressions raised to a power, where each entry is the sum of the two directly above it.

What equation does this parent graph represent?

y=x²

What equation does this parent graph represent?

y=x

What equation does this parent graph represent?

y=x³

What equation does this parent graph represent?

y=1/x

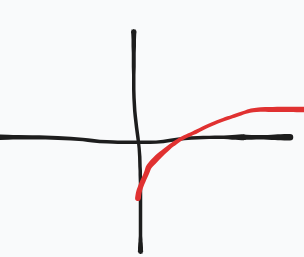
What equation does this parent graph represent?

• y=log₂x

• y=lnx (this one will appear to grow slower on an actual graph)

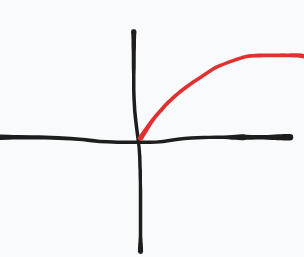
What equation does this parent graph represent?

y= squareroot of x (notice how it starts at the origin and not below)

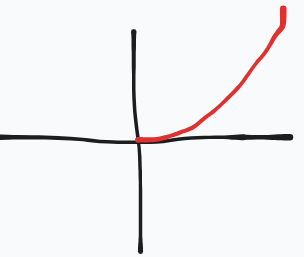
What equation does this parent graph represent?

• y=2^x

• y=e^x

(does not start at the origin contrary to my by bad drawing)

f ◦ g(x)

Composition of functions, where the output of g(x) becomes the input for f(x). also expressed as f(g(x))

An inverse function is…

a function that undoes the action of another function. If f(x) is a function, then its inverse, denoted f⁻¹(x), satisfies f(f⁻¹(x)) = x.

Rules for semi log plots

• the y-axis is a logarithmic scale usually powers of 10

• the beginning y-value is 10⁰ =1

• a data set that behaves in an exponential model will appear linear when the y-axis is logarithmically scaled

Key features of the parent equation y=sin(x)

• a period of 2π

• starts at origin and oscillates between -1 and 1.

Key features of the parent equation y=cos(x)

• a period of 2π

• starts at 1 and oscillates between -1 and 1

Key features of the parent equation y=tan(x)

• a period of π

• starts at the origin

• vertical asymptotes at π/2 +kπ, where k is an integer.

key features of the parent equation y=csc(x)

• a period of 2π

• undefined at π + kπ, where k is an integer.

• oscillates between -∞ and -1 or 1 and ∞.

Key features of the parent equation y=sec(x)

• a period of 2π

• undefined at π/2 + kπ, where k is an integer.

• oscillates between -∞ and -1 or 1 and ∞.

Key features of the parent equation y=cot(x)

• a period of π

• undefined at kπ, where k is an integer.

• oscillates between -∞ and ∞.

Even trigonometric functions are…

• cosine

• sec

Odd trigonometric functions are…

• sine

• csc

• tan

• cot

Pythagorean trig identities (there are 3)

• sin²(x) + cos²(x) = 1

• 1 + tan²(x) = sec²(x)

• 1 + cot²(x) = csc²(x)

Reciprocal trig identities

• csc(x) = 1/sin(x)

• sec(x) = 1/cos(x)

• cot(x) = 1/tan(x) = sin(x)/cos(x)

Any reciprocals multiplied together = 1

Double angle trig identities

sin(2x) =

• 2sin(x)cos(x)

cos(2x) =

• cos²(x) - sin²(x)

• 2cos²(x)-1

• 1 - 2sin²(x)

Trig angle sum formulas…

sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)

cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b).

Trig angle Difference formulas

sin(a - b) = sin(a)cos(b) - cos(a)sin(b)

cos(a - b) = cos(a)cos(b) + sin(a)sin(b)

A values function in a sin(x) or cos(x) transformation

indicates the height of the wave from the center line to its peak or trough.

Amplitude (absolute value of A)

A= max-min/2

a<0 reflects graph over x axis

B values function in a sin(x) or cos(x) transformation

determines the horizontal shift of the graph. It also affects the period of the wave.

period= 1/frequency = 2pi/B

C values function in a sin(x) or cos(x) transformation

Determines the phase shift of the graph. If C is positive, the graph shifts to the left; if negative, it shifts to the right.

D values function in a sin(x) or cos(x) transformation

Determines the vertical shift of the graph. A positive D shifts the graph upward, while a negative D shifts it downward.

D= max+min/2

A values function in a tan(x) transformation

Determines the vertical stretch or compression of the graph. A positive A value increases the steepness, while a negative A flips the graph.

B values function in a tan(x) transformation

Period = pi/b

C values function in a tan(x) transformation

Determines the horizontal shift of the graph. A positive C value shifts the graph to the left, while a negative C value shifts it to the right.

D values function in a tan(x) transformation

Determines the vertical shift of the graph. A positive D value shifts the graph upward, while a negative D value shifts it downward.

To change from polar to rectangular coordinates, use these formulas….

x = r cos(θ)

y = r sin(θ)

(where r = the radius and θ = angle in degrees or radians).

To change from rectangular to polar coordinates use these formulas…

x²+y²=r²

tan(x)=y/x (where x does not equal zero)

when r=f(x) is increasing and r-value is positive…

distance from the origin is increasing

when r=f(x) is increasing and r-value is negative…

distance from the origin is decreasing

when r=f(x) is decreasing and r-value is positive…

distance from the origin is decreasing

when r=f(x) is decreasing and r-value is negative…

distance from the origin is increasing

r(x)=x in the polar form makes a…

spiral with increasing radius

r=a in polar form makes a…

circle with radius a, centered on the pole

r = acos(x) in polar form makes a…

a circle centered on the right or left side of the pole, with diameter a.

r = asin(x) in polar form makes a…

a circle centered above or below the pole, with diameter a.

Cardiods occur when…

the equation is of the form r = a ± a cos(θ) or r = a ± a sin(θ).

(a/b=1)

occurs when a verticle shift happens in rectangular form, causing the maximum or minimum to “bounce” off of the x axis instead of crossing it

Convex limacons aka dimpled cardioids occur when…

the equation is of the form r = a ± b cos(θ) or r = a ± b sin(θ) where

b < a. (and both are greater than zero)

occurs when a vertical shift happens in rectangular form, where the function never touches the x-axis, causing a dimple that never touches the pole.

Limacon with inner loop occurs when…

the equation is of the form r = a ± b cos(θ) or r = a ± b sin(θ) where

b > a (and both are greater than zero)

occurs when a vertical shift happens in rectangular form, where the function crosses the x axis, but not at the point of inflection, causing an inner loop.

when would a rose occur in polar form…

when there is a horizontal dilation in rectangular form.

The equation is r = a sin(nθ) or r = a cos(nθ), where n is a positive integer. Roses have petals based on the integer value of n

if n is even, there are 2n petals; if n is odd, there are n petals.