STP 420 Exam 2

Conditional Probablity

P(A|B) = P(A n B)/P(B)

Long Run Probability

As the number of trials increases, the average of the results will get closer and closer to the expected value. (Law of large numbers)

General Addition Rule

P(A u B) = P(A) + P(B) - P(A n B)

Special Addition Rule

P(A u B) = P(A) + P(B) when independent

Expected Value

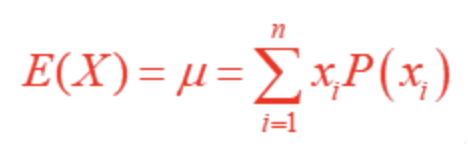
Var[X]

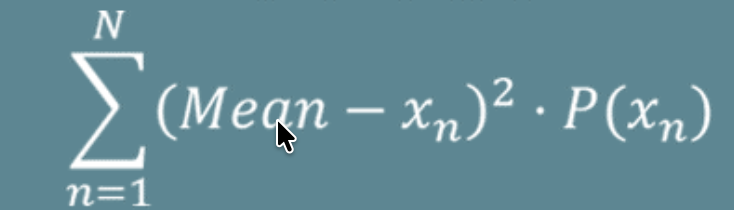
Properties of E[X]

• E[c] = c

• E[g₁(x) + g₂(x)]  = g₁E[x] + g₂E[x]

• E[cg(x)] = cE[g(x)]

Properties of Var[x}

• Var[c] = 0

• Var[X + Y] = Var[X] + Vary[Y] only if X and Y are independent

  • if dependent: Var[X] + Var[Y] + 2psqrt(Var[X])sqrt(Var[Y])

• Var[aX + b] = a²Var[X]

CLT Requirements

We can assume a normal distribution of a sample if:

• population is normally distributed

• sample size is sufficient (n >= 30)

Confidence Interval Requirements

Check CLT

Z_a/2

a = 1 - confidence level

• 90% confidence: 1 - .90 = 0.1 => 0.1/2 = 0.05

• z_0.05 = 1.96

Margin of Error

z_a/2*(sd/sqrt(n))

Confidence Interval

point estimate ± margin of error

Necessary sample size for confidence level with certain margin of error

n = ((z_a/2)²(sd)^²)/(E)²

• round up for integer value